Tétel:
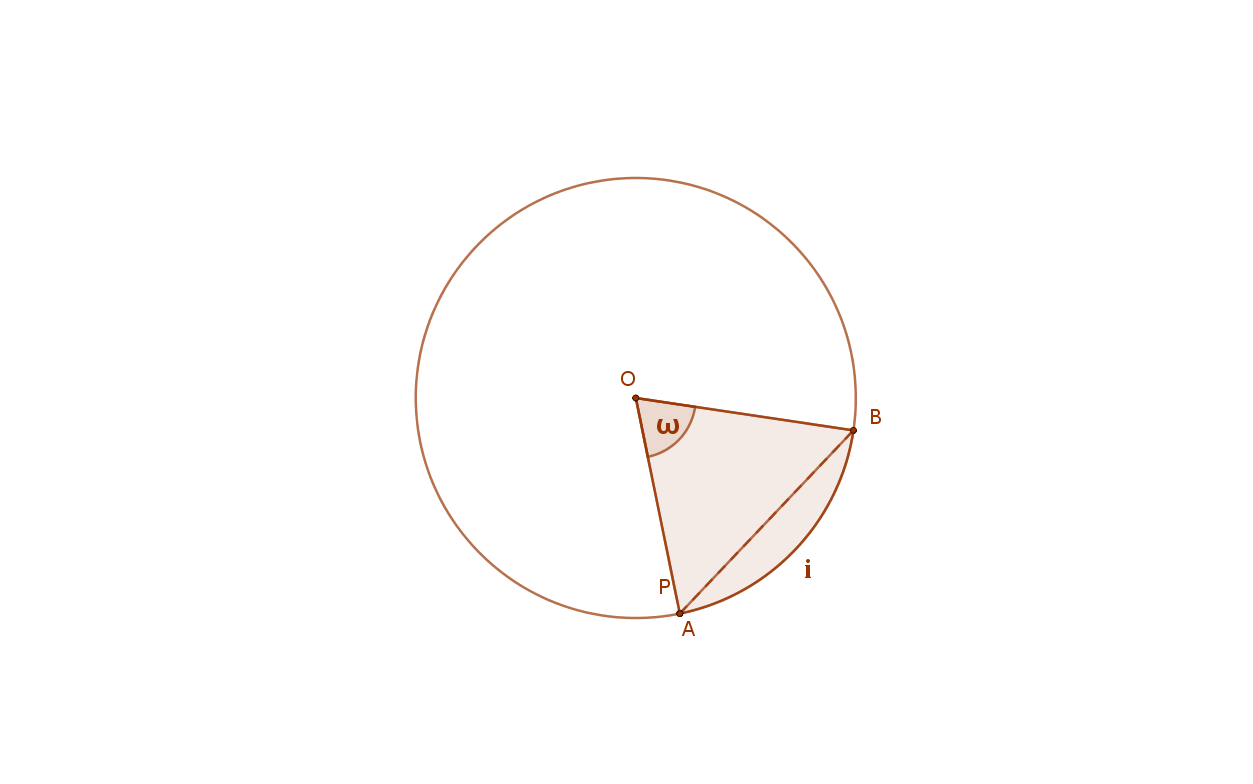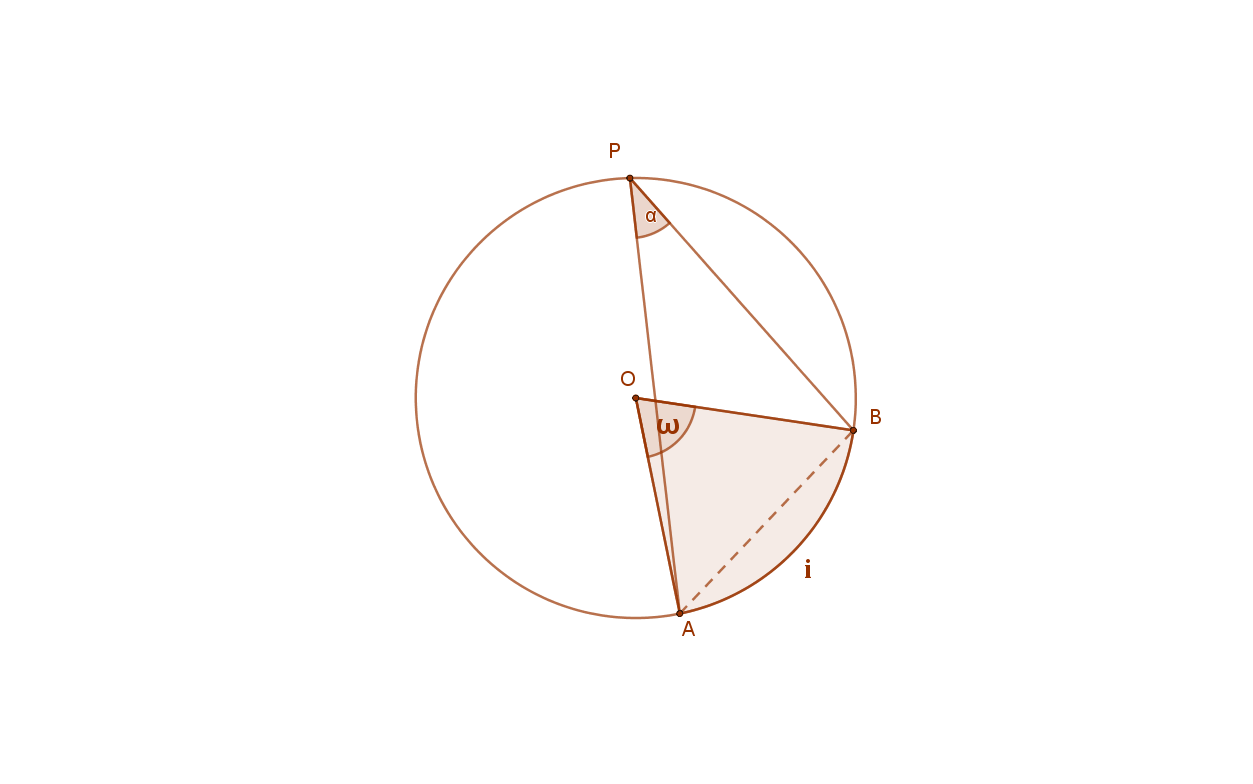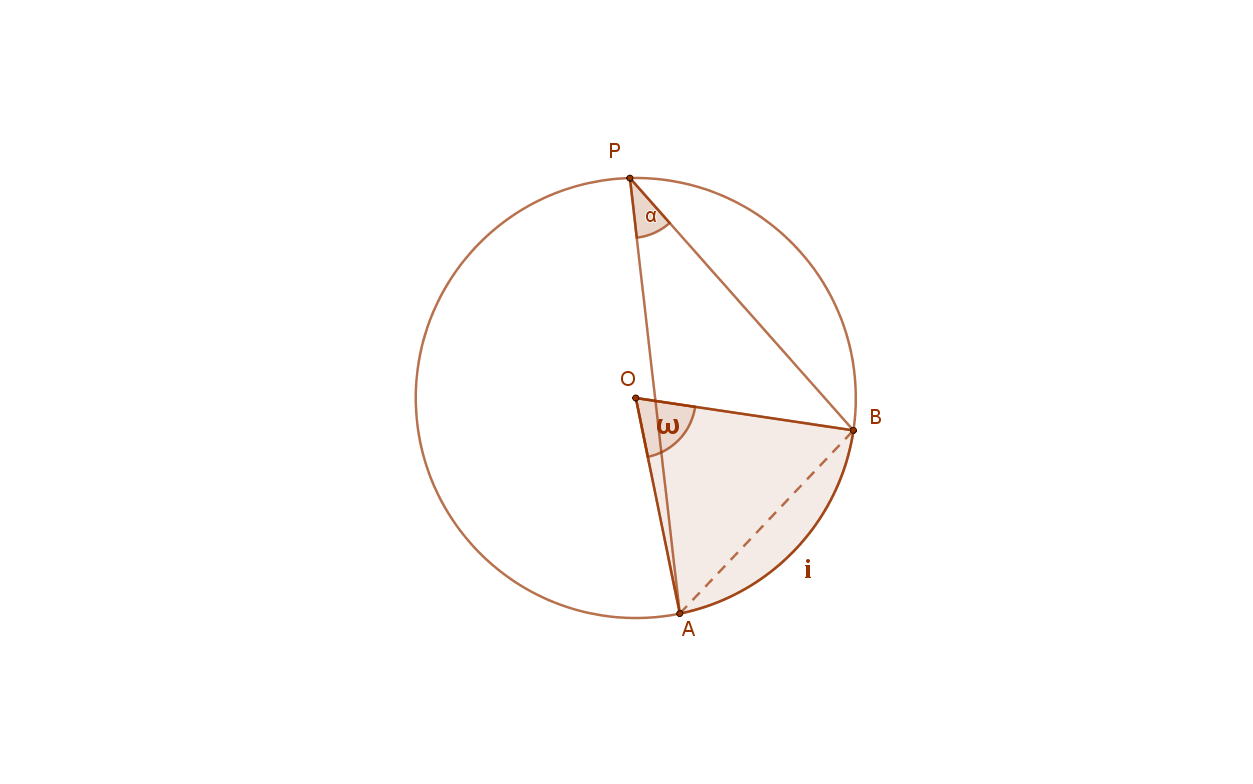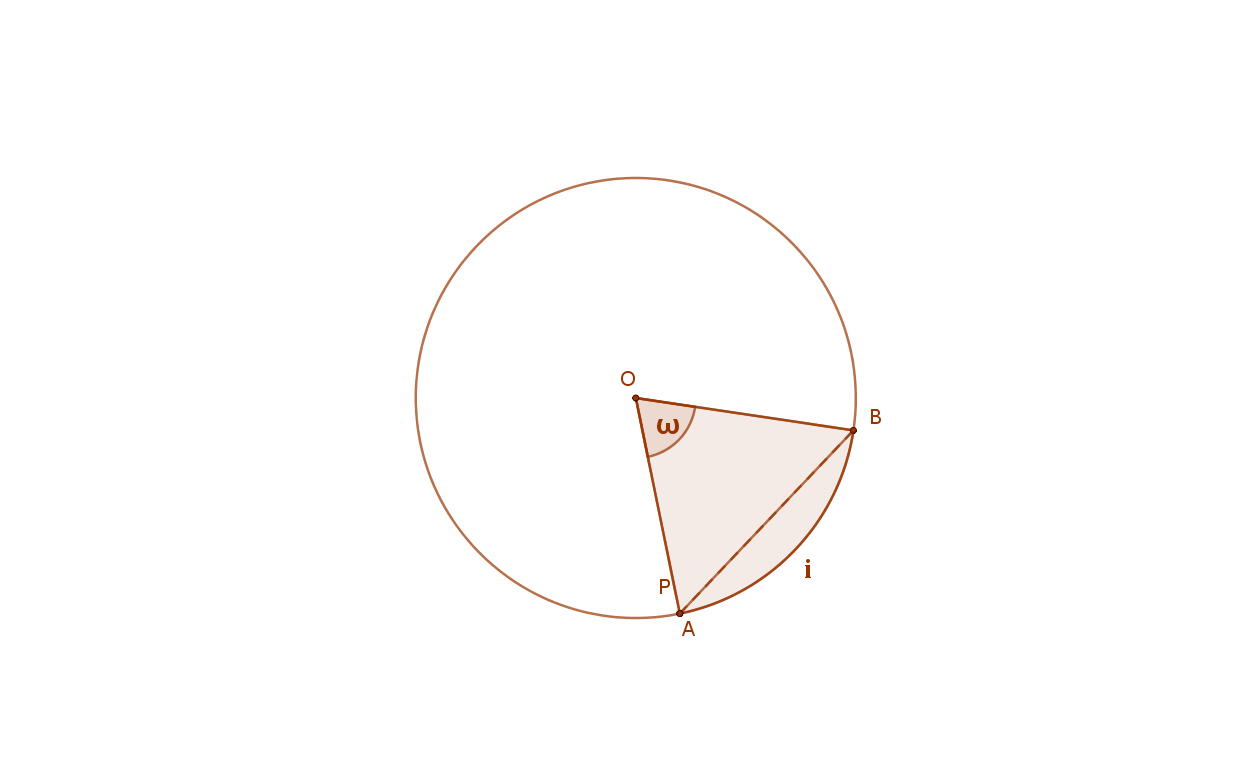
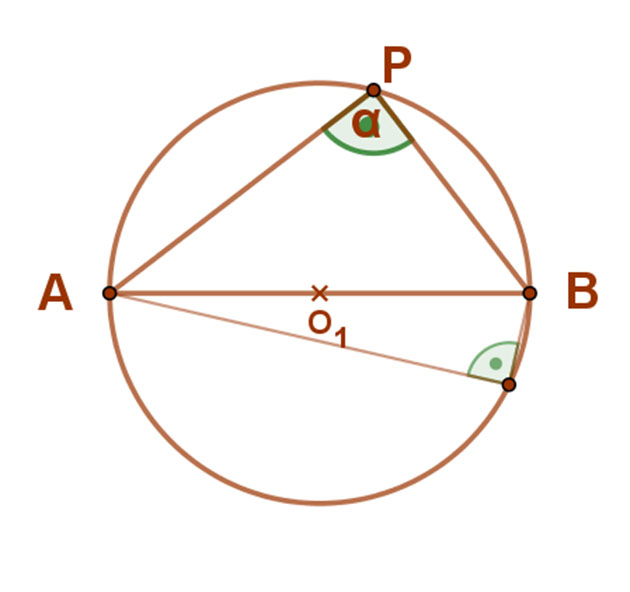
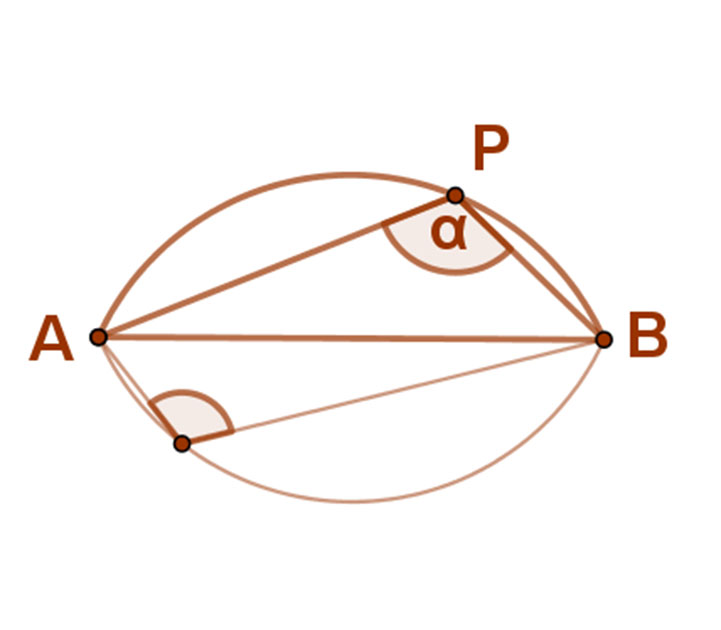
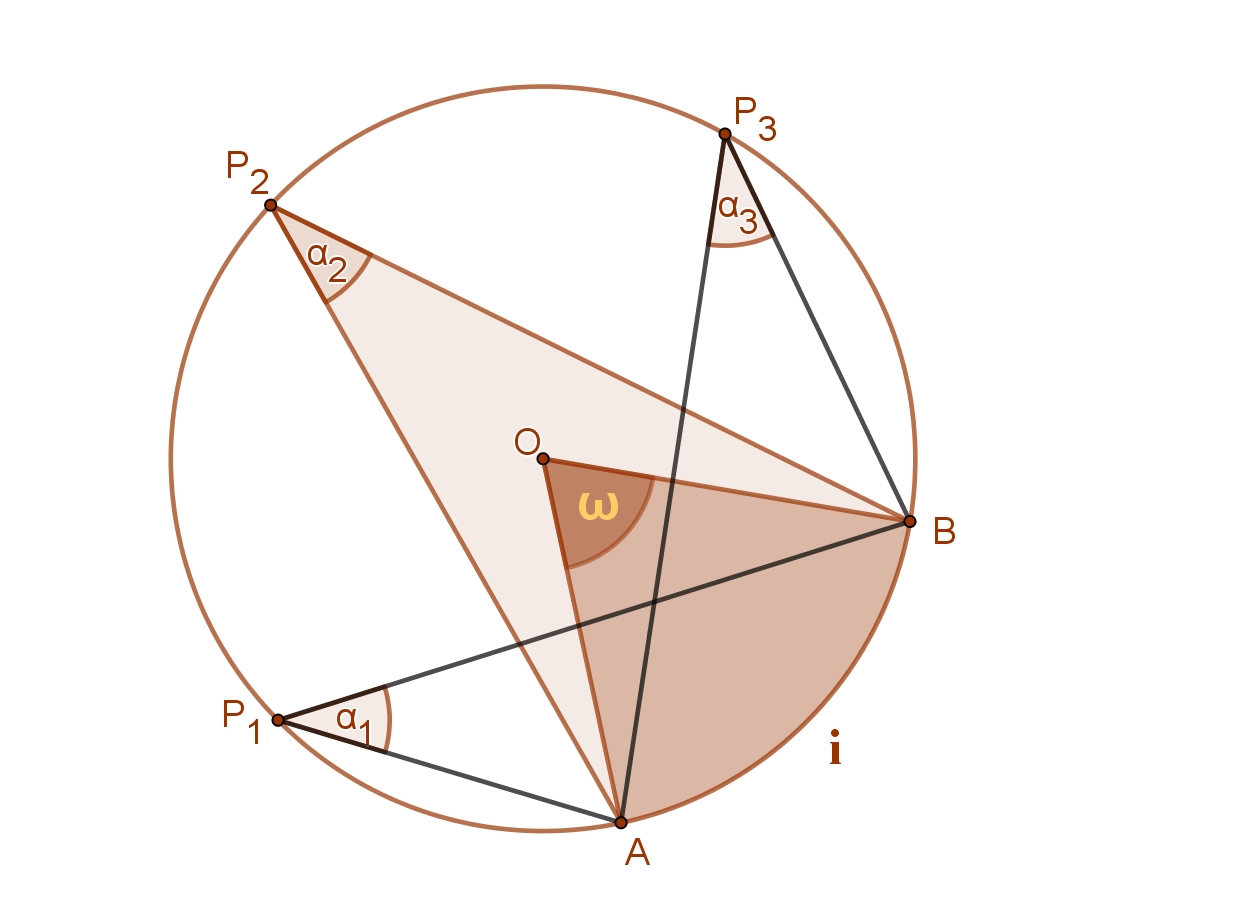Egy körben az ugyanazon ívhez tartozó kerületi szögek egyenlők.
Ez a tétel a kerületi és középponti szögek tételéből következik.
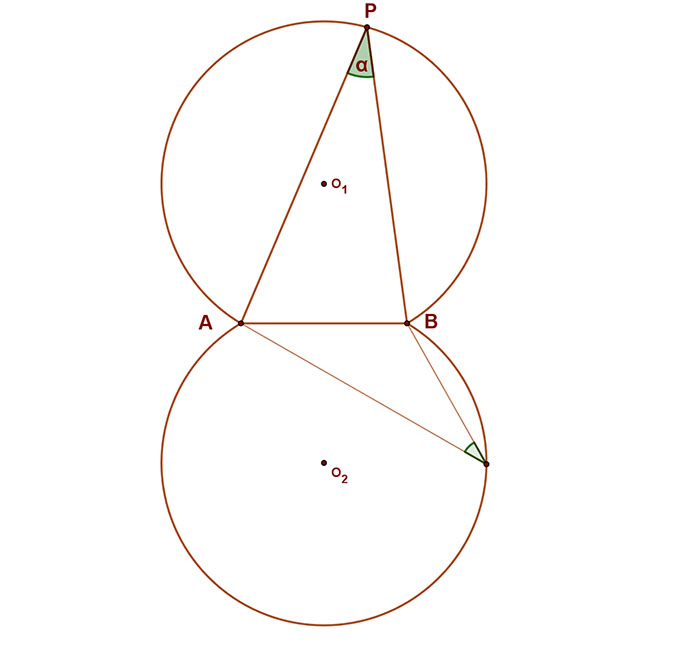
Ebből a tételből viszont azonnal következik az a kérdés, hogy mi azoknak a pontoknak az összessége (mértani helye) a síkban, amelyekből egy adott AB szakasz adott a szög alatt látszik?
Tétel:
A síkon azoknak a pontoknak a halmaza, amelyekből egy adott AB szakasz adott (0<a<180°) szög alatt látszik, két szimmetrikus körív (látókörív).
Az adott szakasz a két szimmetrikus körív közös húrja. Ennek végpontjai nem tartoznak a látószögkörívhez.
|
|
|
|
Látókörívek szerkesztése.
Adott egy AB szakasz és egy α szög.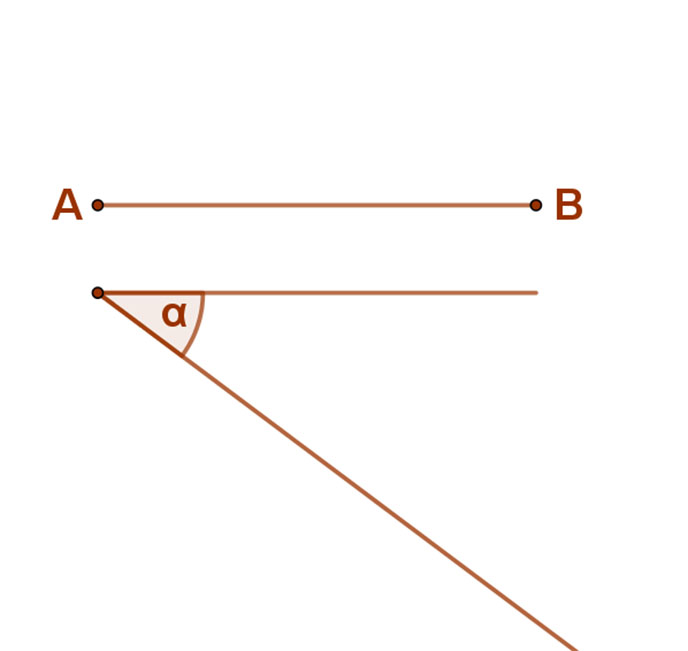
1. Szerkesszük meg az adott AB szakasz felezőmerőlegesét. Ez áthalad a keresett kör középpontján.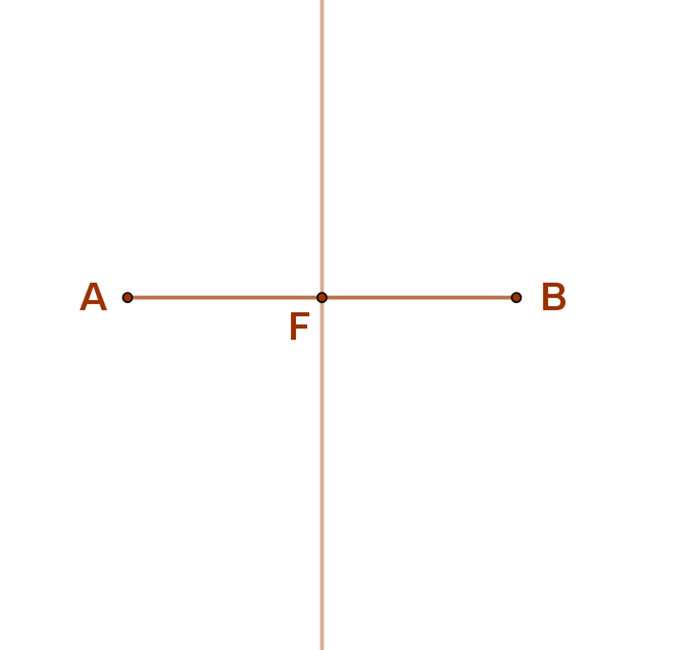
2. Az adott AB sz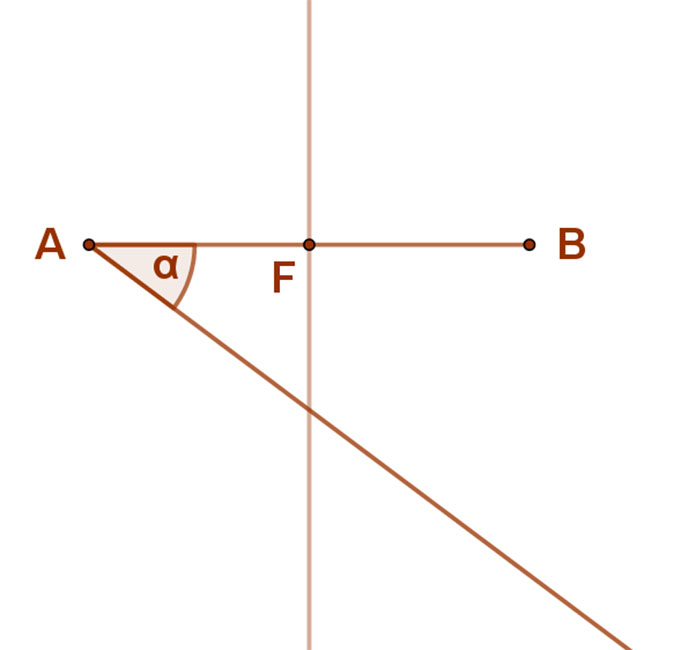
akasz A vagy B végpontjába megszerkesztjük (odamásoljuk) az adott a szöget.
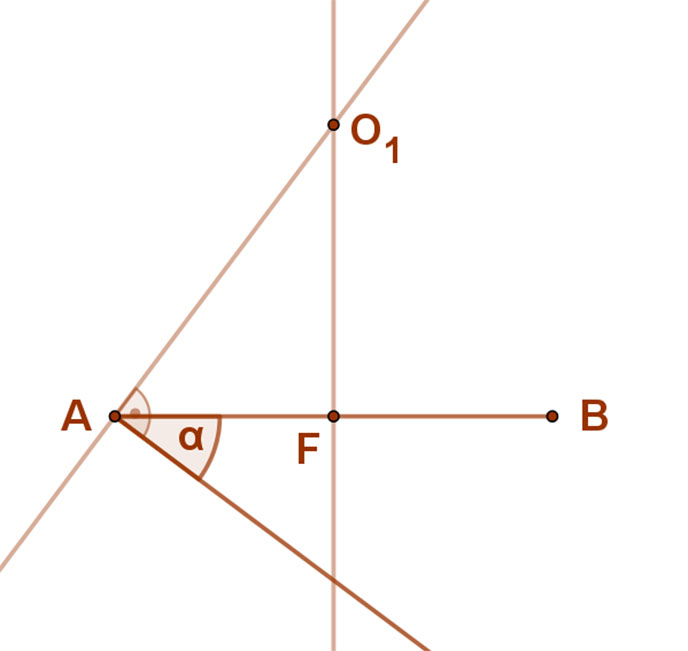3. Ugyanebben a pontban az új szögszárra (ez a kör érintője) merőlegest emelünk. Ez és az AB szakasz felező merőlegese kimetszi a keresett középpontot. (O1)
4. A kapott O1 pont körül meghúzzuk a az AB látókörívet.
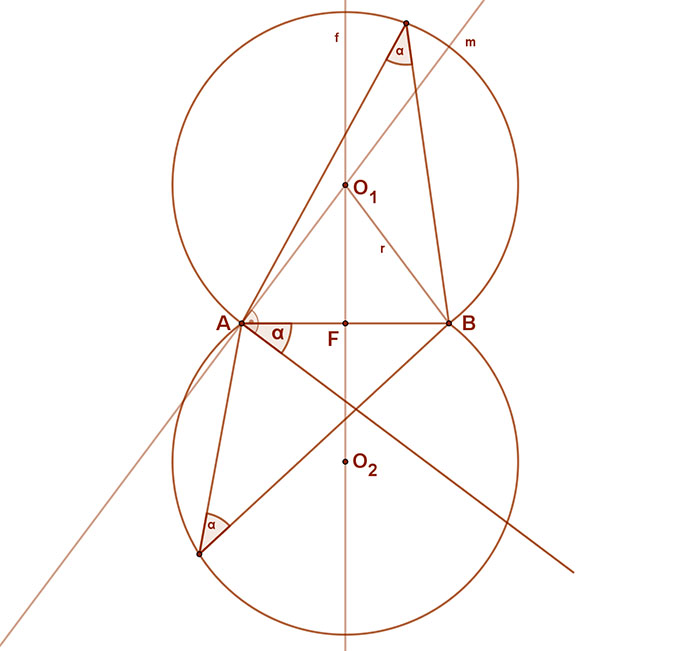5. Ezt tükrözve az AB szakasz egyenesére, megkapjuk a látókörív párját.
Comments are closed, but trackbacks and pingbacks are open.