Szabályos sokszögek

Definíció:

Szabályos sokszögeknek nevezzük azokat a sokszögeket, amelyeknek minden oldala egyenlő hosszú és minden szöge egyenlő nagyságú.

Példa: A mellékelt animációban láthatunk néhány „n” oldalú szabályos sokszöget. (n=3, …. ,12)

Megjegyzés: A szabályos sokszögek definíciója természetes rokonságot mutat a szabályos testek (szabályos poliéderek)  definíciójával. Mondhatjuk azt is, hogy a szabályos sokszögek a 3D-s szabályos poliéderek 2D-s megfelelője. Van azonban egy lényeges különbség:  mindössze öt szabályos poliéder van, míg végtelen számú szabályos sokszög lehetséges.

Szabályos sokszögek tulajdonságai:

A szabályos sokszögek tengelyesen szimmetrikusak. Egy „n” oldalú szabályos sokszögnek „n” darab szimmetriatengelye van.

Ha az oldalak száma páros, akkor a szimmetriatengely a szemközti oldalak felezőpontjain halad át.
Ha az oldalak száma páratlan, akkor a szimmetriatengely az egyik oldal felezőpontján és a szemközti csúcson halad át.

A szabályos sokszögek szimmetriatengelyek metszéspontjára nézve forgásszimmetrikusak.

Páros oldalszámú szabályos sokszögek a szimmetriatengelyek metszéspontjára nézve középpontosan szimmetrikusak.

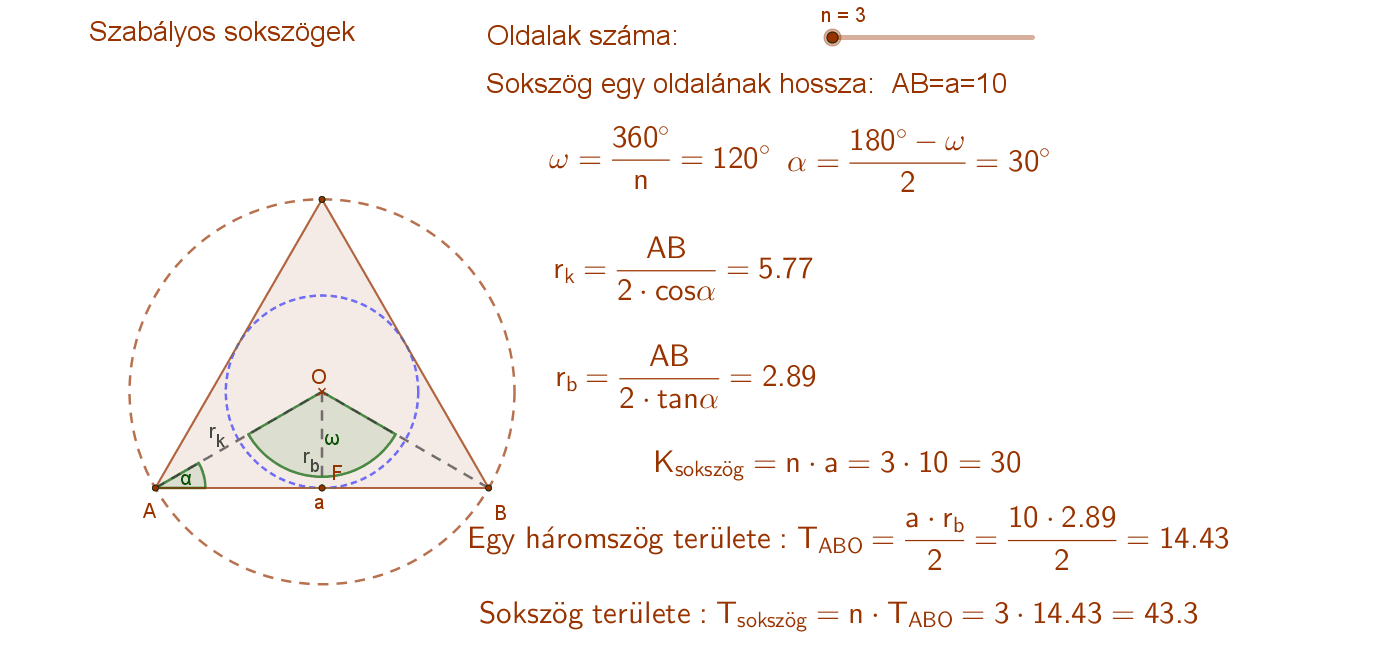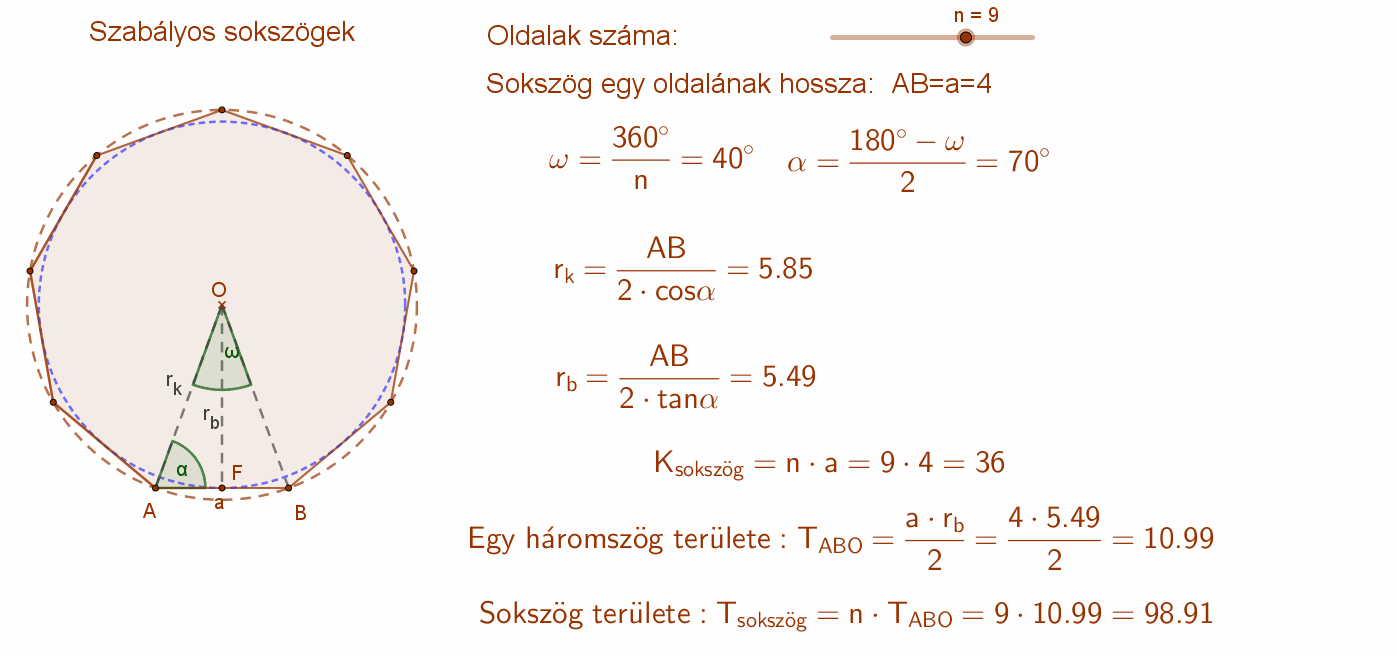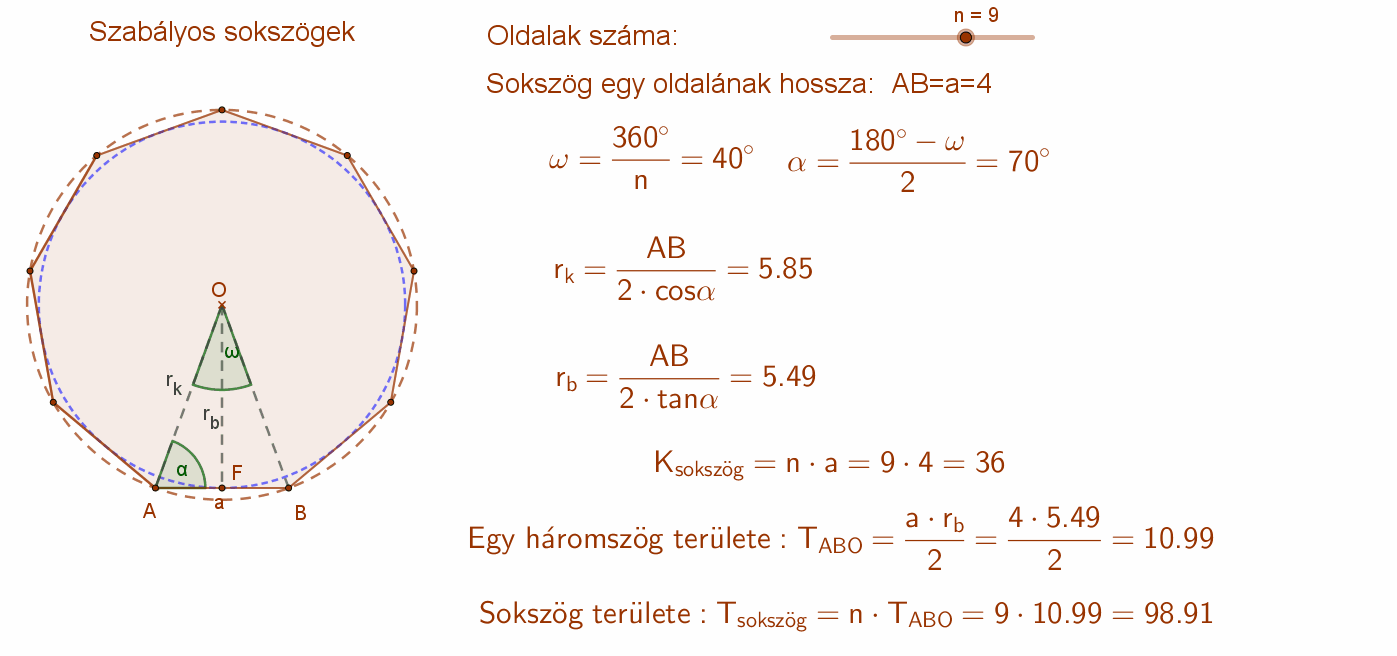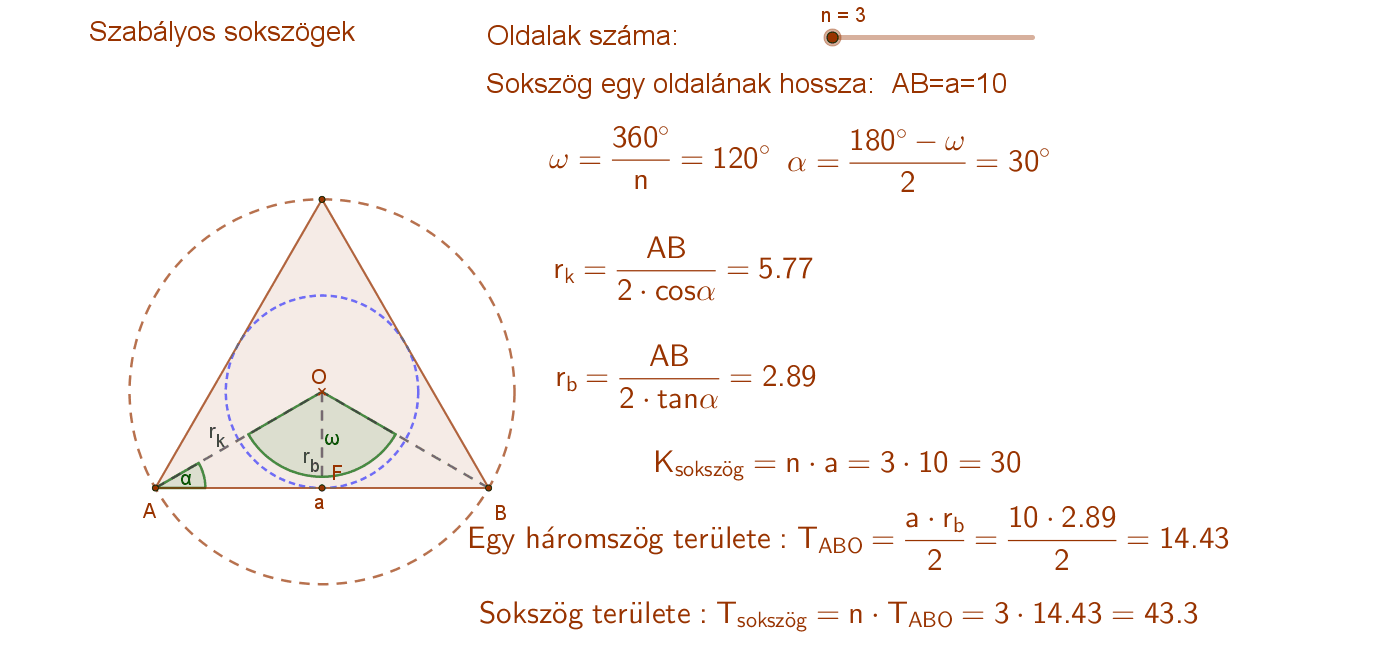
Mivel minden sokszög belső szögeinek összege ​\( \left( n-2 \right) ·180^{∘} \)​ , ezért a szabályos sokszögek csúcsainál lévő belső szögek nagysága: ​\( \frac{(n-2)·180^{∘}}{n} \). Ebből következik, hogy minden szabályos sokszög konvex.

A szabályos sokszögek köré (csúcsain áthaladó) kör írható. Ennek középpontja („O”) a szimmetriatengelyek metszéspontja, sugara (r_k) pedig a középpontot a sokszög csúcsaival összekötő szakasz.

Minden szabályos sokszögeknek van beírt  (oldalait érintő) köre. Ennek középpontja („O”) a szimmetriatengelyek metszéspontja, sugara (r_b) pedig a középpontból az oldal felezőpontjába állított merőleges szakasz.

A szabályos sokszögek kerülete az oldalak számának és egy oldal hosszának a szorzat. K=n⋅a.

Ha az n oldalú szabályos sokszög középpontját összekötjük a sokszög csúcsaival, akkor n db egybevágó, egyenlőszárú háromszöget kapunk.
Egy ilyen háromszög területe: Az oldal hossza és a beírt kör sugara szorzatának a fele.
Másképp: A köré írt kör sugarának négyzete, szorozva a szár szög (középponti szög) szinuszával és osztva kettővel.
A sokszög területét megkapjuk, ha egy háromszög területét megszorozzuk az oldalak számával.

Szabályos sokszögekkel sokszor, sok helyen találkozhatunk.

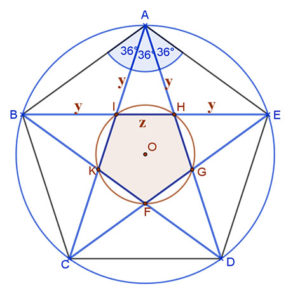
A szabályos ötszöget már az ókorban is ismerték. Pitagorasz-csillag.	Szabályos ötszög a tengeri csillag.	Szabályos ötszög található egyes nemzetek zászlóin.
Szabályos hatszög. Méhek a méhkaptárban.	Szabályos hatszög egy faszerkezetben, benne egy szabályos háromszög.	Szabályos hatszög, mint egy  szövetminta.

Szabályos sokszögek szerkeszthetősége:

Egy adott oldalú (vagy adott körbe illesztendő) szabályos háromszög, egy négyzet vagy egy szabályos hatszög megszerkesztése nem szokott gondot jelenteni a diákoknak. Ugyanez nem mondható el például a szabályos tíz- vagy ötszög esetén, bár ezek is viszonylag könnyen szerkeszthetők.

Ugyanakkor egy szabályos 17 oldalú sokszög szerkesztése már igen komoly feladat. Gauss, a matematika egyik legnagyobbika azt kérte, hogy sírjára egy szabályos 17-szöget véssenek. A szerkesztés euklideszi értelemben is végrehajtható, de be kell vallanom, én magam nem tudok 17 oldalú szabályos sokszöget szerkeszteni. Talán nem kell emiatt senkinek sem szégyenkeznie, hiszen Gauss ugyan bebizonyította, hogy a szabályos 17-szög szerkeszthető, de ő maga nem mutatott rá konkrét szerkesztést. Az első ilyen szerkesztést Erchinger nevű matematikus hajtotta végre, néhány évvel Gauss halála után.

A matematikusok már kimutatták, hogy mely szabályos sokszögek szerkeszthetők euklideszi értelemben és melyek nem.
Az természetes, hogyha egy „n” oldalú szabályos sokszög szerkeszthető, akkor az n⋅2^k (k ∈ ℤ⁺) sokszög is szerkeszthető.

Nézzük tehát az első csoportot. n=3, 6, 12,… stb. oldalú sokszögek családját! A szabályos hatszög szerkesztése talán a legkönnyebb, ebből a szabályos háromszög és például a szabályos 12-szög könnyen előállítható.

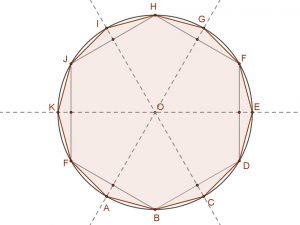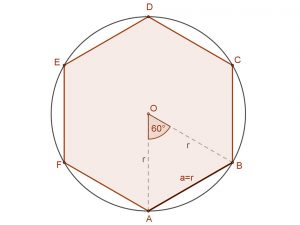
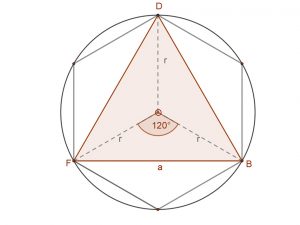
Szabályos hatszög	Szabályos hatszögből szabályos háromszög. Minden második csúcsot összekötve, fele akkora oldalszámú sokszöget kapunk.	Szabályos 12-szög. A szabályos hatszög köré írt körön az egyes oldalak felező merőlegesei metszik ki az új csúcsokat.

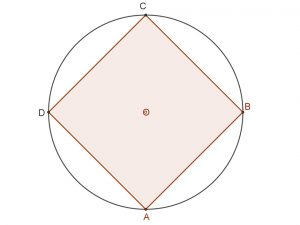
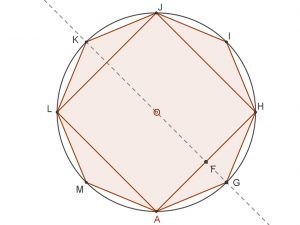
A következő csoport: n= 4, 8, 16, …

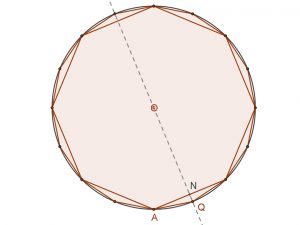Négyzet	Szabályos nyolcszög	Szabályos 16-szög

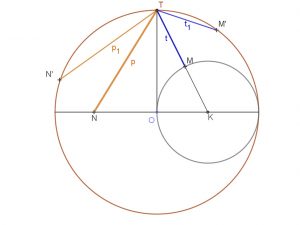
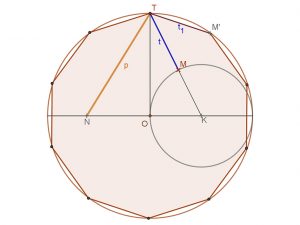
Euklideszi értelemben szerkeszthetők az n=5, 10, 20,… oldalú sokszögek is. Ezeknek a sokszögeknek a szerkesztése az aranymetszésen alapszik.
Lásd: Hámori Miklós: „Arányok és talányok” című könyve. Typotex kiadó 1994.

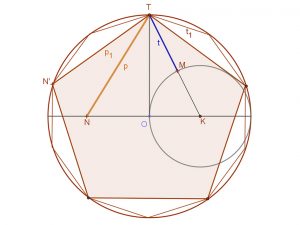Szabályos tíz- és ötszög oldalainak szerkesztése az aranymetszésen alapul.	Szabályos tízszög.	A szabályos tízszögből a szabályos ötszög szerkeszthető.

De szerkeszthetők például az n=15 vagy az n=17 oldalú szabályos sokszögek is.

Ugyanakkor euklideszi szerkesztéssel nem állítható elő például a n=7, az n=9, az n=11, az n= 23, vagy az n=25 oldalú szabályos sokszög sem.

Itt is igaz, hogy ha egy „n” oldalú sokszög euklideszi értelemben nem szerkeszthető, akkor az n⋅2^k (k ∈ ℤ⁺) sokszög sem szerkeszthető. Tehát nem szerkeszthetők euklideszi értelemben az n=7, 14, 28, … oldalú szabályos sokszögek. De ugyan így nem szerkeszthetők a n=9, 18, 36, …  vagy az n=11, 22, 44, … oldalú szabályos sokszögek sem.

A szabályos sokszögek szerkeszthetőségével kapcsolatban lásd: https://hu.wikipedia.org/wiki/Szerkeszthet%C5%91_soksz%C3%B6gek

A szabályos sokszögek szerkesztése szoros kapcsolatban van a szögek szerkesztésével.

Hiszen ha egy szabályos sokszög szerkeszthető, akkor a két szomszédos csúcshoz középponti szög is szerkeszthető.
És persze fordítva, ha egy szabályos sokszög nem szerkeszthető, akkor a két szomszédos csúcshoz tartozó középponti szög sem szerkeszthető.

Például: a ω=360º/17 szerkeszthető, pedig a 360º/17 ≈ 21,18º. Ugyanakkor például a ω=360º/9=40º nem állítható elő euklideszi szerkesztéssel.

Megjegyzés:

A fenti ábrákon ugyan találkoztunk n=7, n=9 és n=11 oldalú „szabályos” sokszögekkel, de ezeket a számítógépes program állította elő. Tekinthetők ezek jó közelítő szerkesztéseknek, de ezek nem euklideszi értelemben vett szerkesztések.