Az „n” oldalú konvex sokszög belső szögeinek összege, átlóinak száma

Definíció:

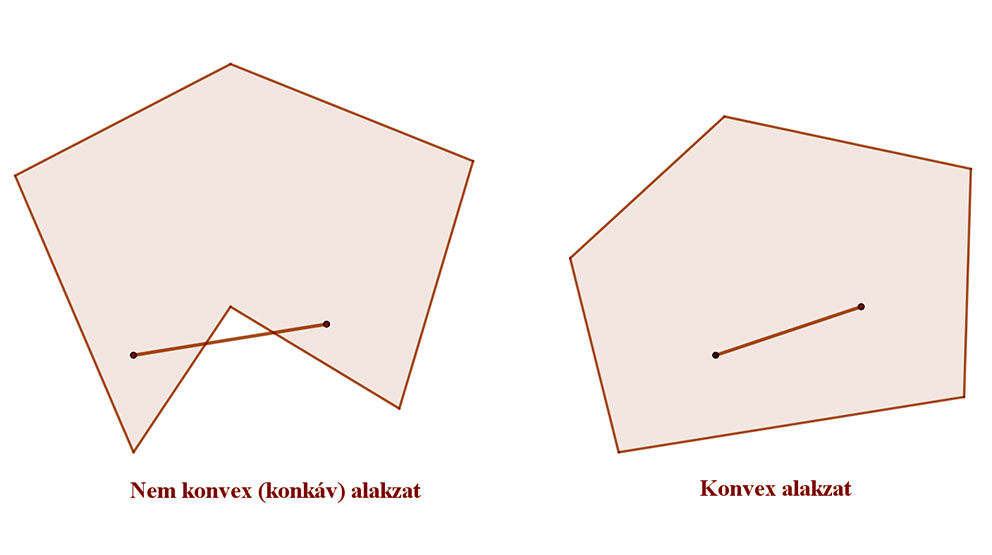
Egy alakzatot konvexnek mondunk, ha bármely két pontjukkal együtt a két pontot összekötő szakasz valamennyi pontját is tartalmazzák.

Definíció:

Sokszögek olyan síkidomok, amelyet csak egyenes szakaszok határolnak.

Definíció:

Átlónak mondjuk a nem szomszédos csúcsokat összekötő szakaszokat (illetve egyeneseket).

Állítás: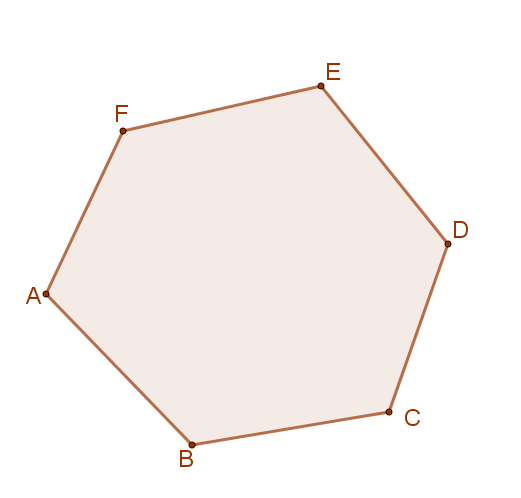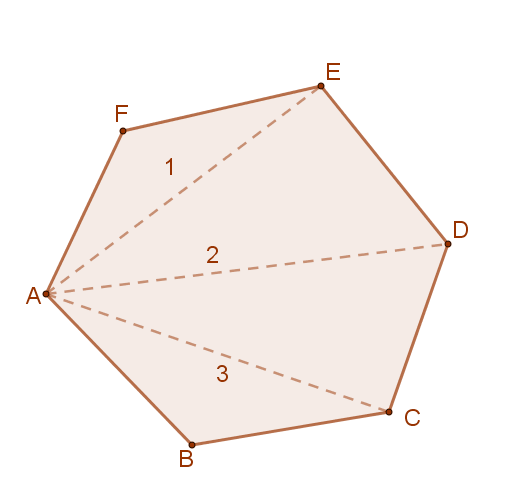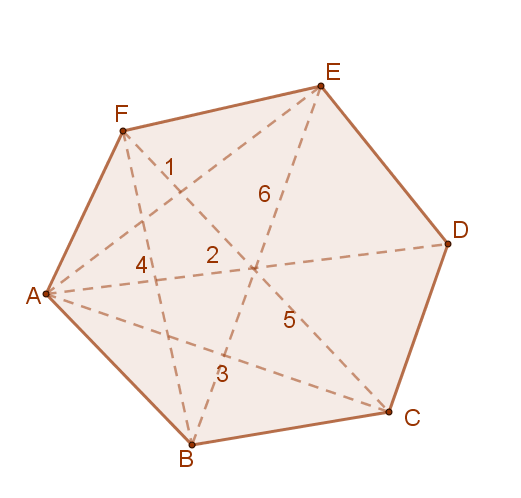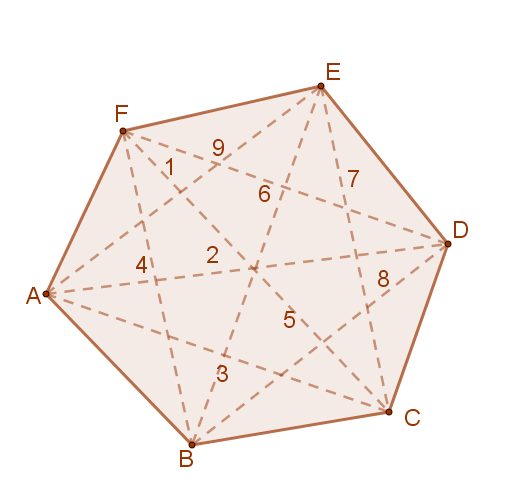

Egy „n” oldalú konvex sokszög átlóinak száma = ​\( \frac{n·(n-3)}{2} \)​.

Például a mellékelt ábrán lévő sokszögnek ​\( \frac{6·(6-3)}{2}=9 \)​ darab átlója van.

Bizonyítás:

A konvex sokszög minden egyes csúcsából (n-3) darab átló húzható, hiszen önmagába és a szomszédos csúcsokba nem húzható átló. A mellékelt ábrán minden csúcsból 3 darab átló indul ki, illetve érkezik oda.
Mivel minden egyes csúcsból (n-3) átló húzható, ezért n darab csúcsból n⋅(n-3) átló lenne húzható. Így azonban  minden átlót pontosan kétszer vettünk figyelembe, a két végpontjánál, ezért az átlók száma=​\( \frac{n·(n-3)}{2} \)​​, az állításnak megfelelően.

Állítás:

Egy „n” oldalú konvex sokszög belső szögeinek összege =(n-2)⋅180°.

Bizonyítás: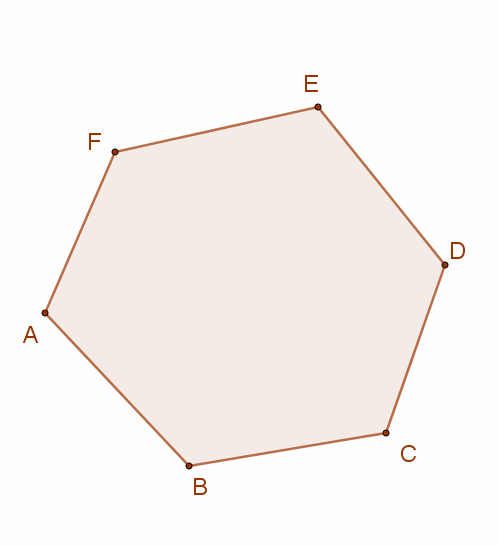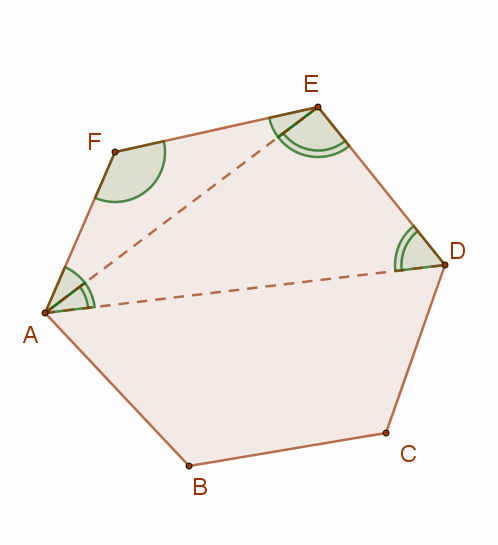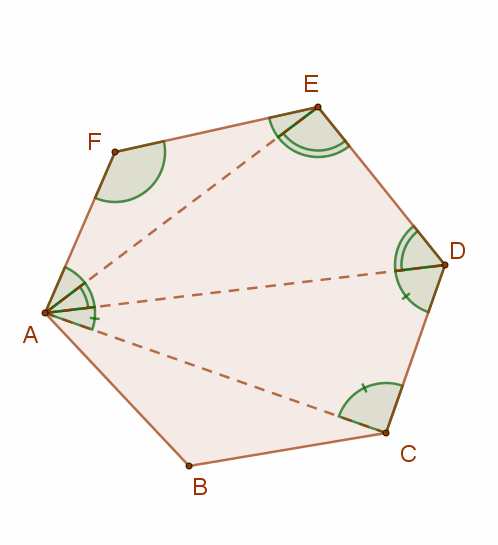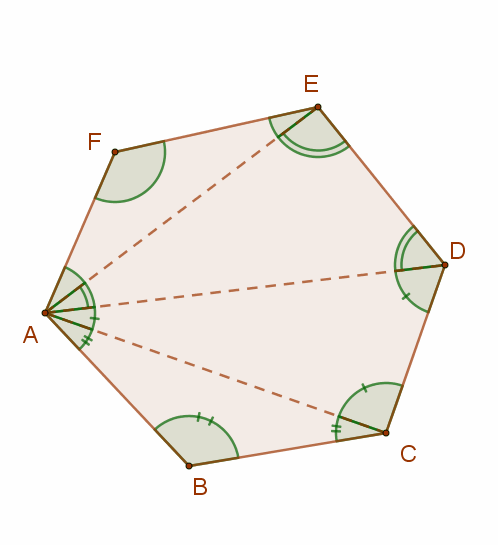

Egy konvex sokszög egy csúcsából (n-3) átló húzható, hiszen önmagába és a szomszédos csúcsokba nem húzható átló.
Az (n-3) darab átló (n-2) darab háromszögre bontja a konvex sokszöget. Mivel egy háromszög szögeinek összege 180°, ezért a sokszög belső szögeinek összege (n-2)⋅180°
A mellékelt ábrán a hatszöget az „A” csúcsból kiinduló 3 darab átló 4 darab háromszögre bontja, ezért minden hatszög belső szögeinek összege=4⋅ 180° =720°.

Állítás:

Egy „n” oldalú konvex sokszög külső szögeinek összege 360°.

Bizonyítás:

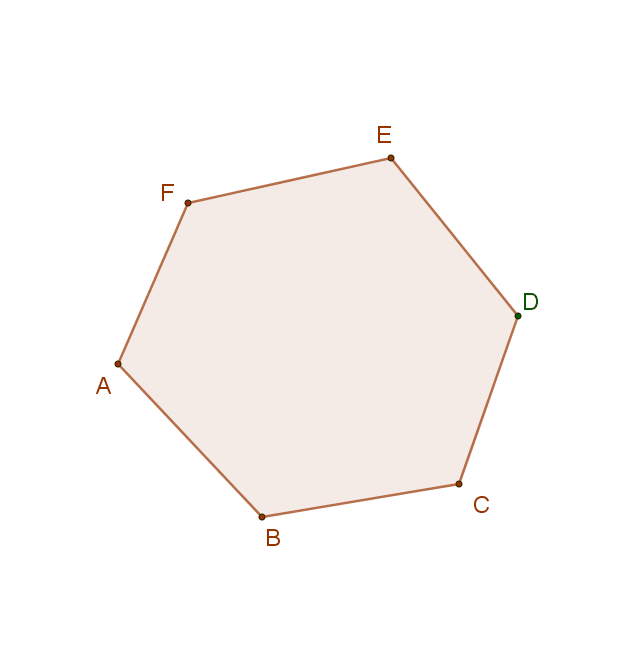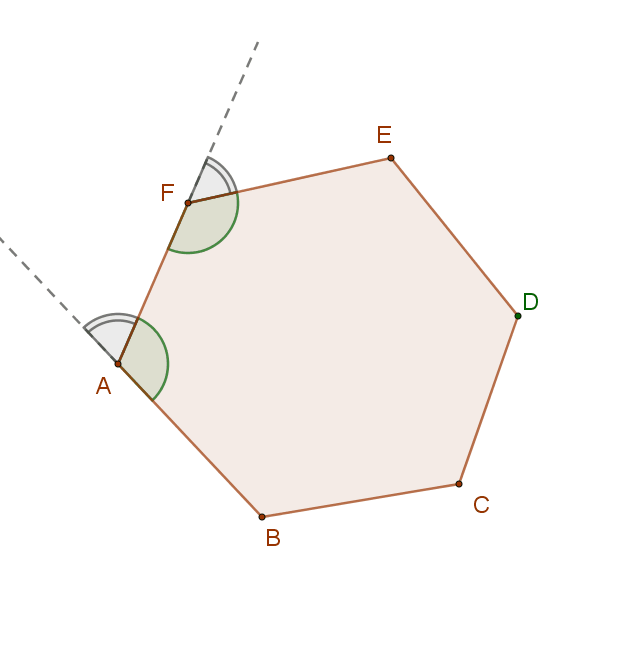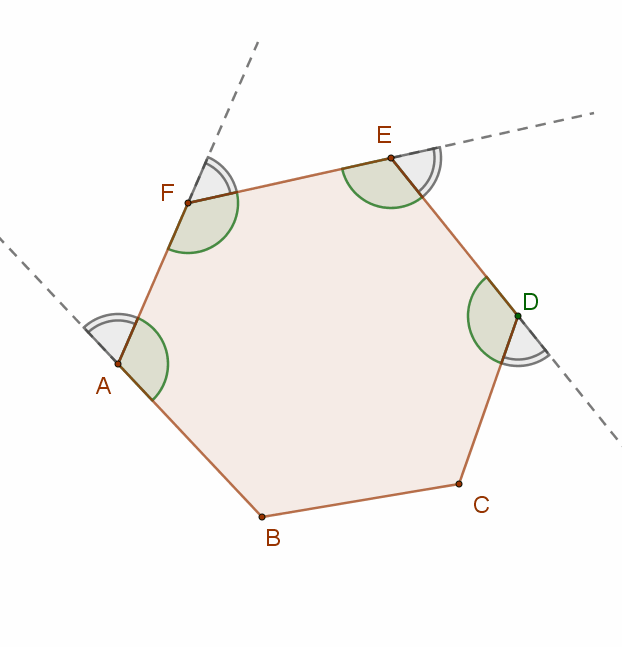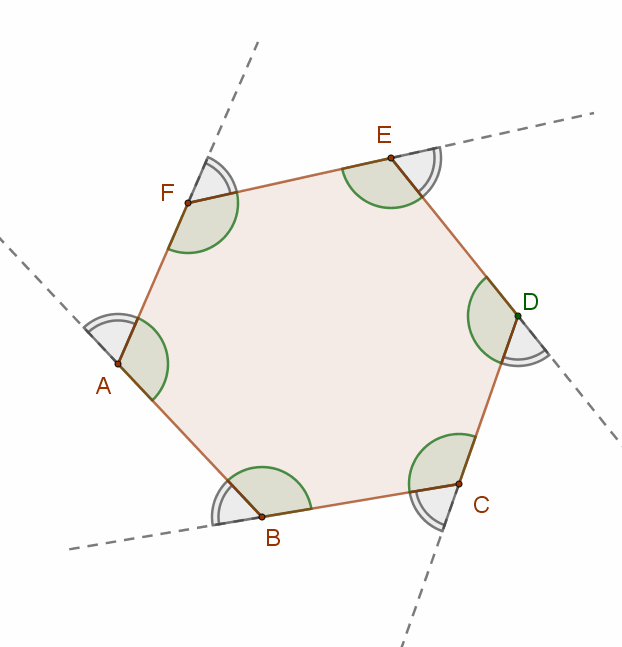
Ennek belátásához húzzuk meg a sokszög minden egyes belső szögéhez tartozó külső szöget.
A belső és a külső szögek összege minden egyes csúcs esetén 180º.
Ezeknek az összeg „n” darab csúcs esetén: n∙180º. Ha ebből kivonjuk a belső szögek összegét, megkapjuk a külső szegek összegét: n∙180º-(n-2)∙180º.

A zárójel felbontása és összevonás után kapjuk az eredményt:

n∙180º-(n-2)∙180º= n∙180º- n∙180º+2∙180º=360º.

Tehát az „n” oldalú sokszög külső szögeinek összege az oldalszámtól függetlenül mindig 360º.