Pont körüli forgatás és tulajdonságai

Definíció:

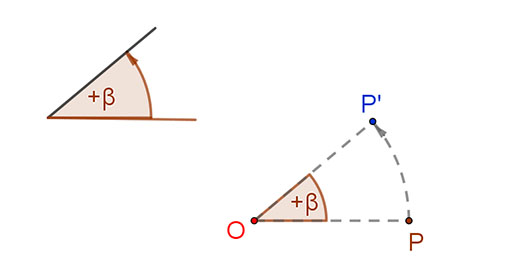Pont körüli forgatásnál adott a síkban egy pont, a forgatás középpontja, és adott egy előjeles szög, amely a forgatás mértékét és irányát adja meg.
Az adott (O) pont körüli adott előjeles szögű (β) forgatás az O ponthoz önmagát, minden más (P) ponthoz azt a képpontot (P’) rendeli, amelyre OP=OP’ és a POP’∠ megegyezik a forgatás szögével (POP’∠ = β).
A pont körüli forgatás kölcsönösen egyértelmű hozzárendelés a sík pontjai között.

A pont körüli forgatás tulajdonságai:

1. Ha a forgatás szöge a teljes szög bármely többszörösétől eltérő mértékű (β≠k∙360°, k∈ℤ), akkor egyetlen fix pont van, a forgatás (O) középpontja.

Ha a forgatás szöge a teljes szög többszöröse (β=k∙360°, k∈ℤ), akkor a sík minden pontja fixpont (identikus transzformáció).

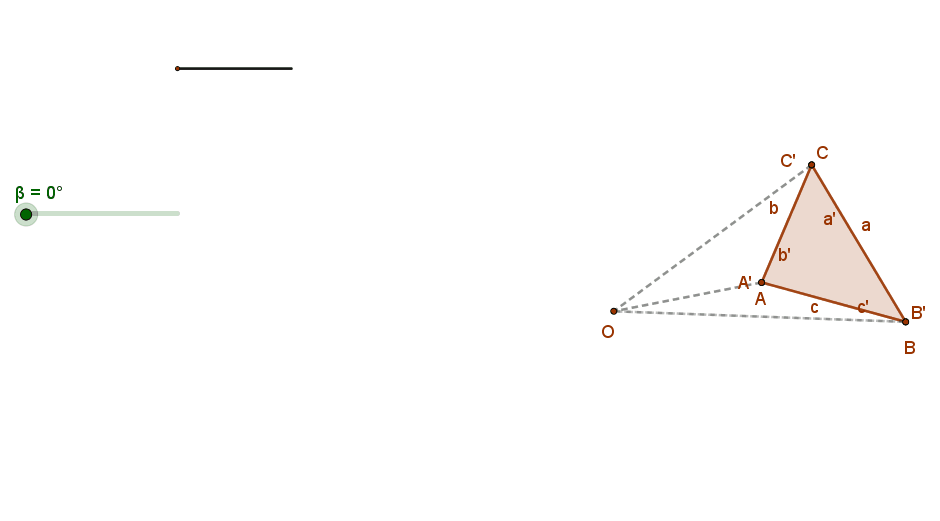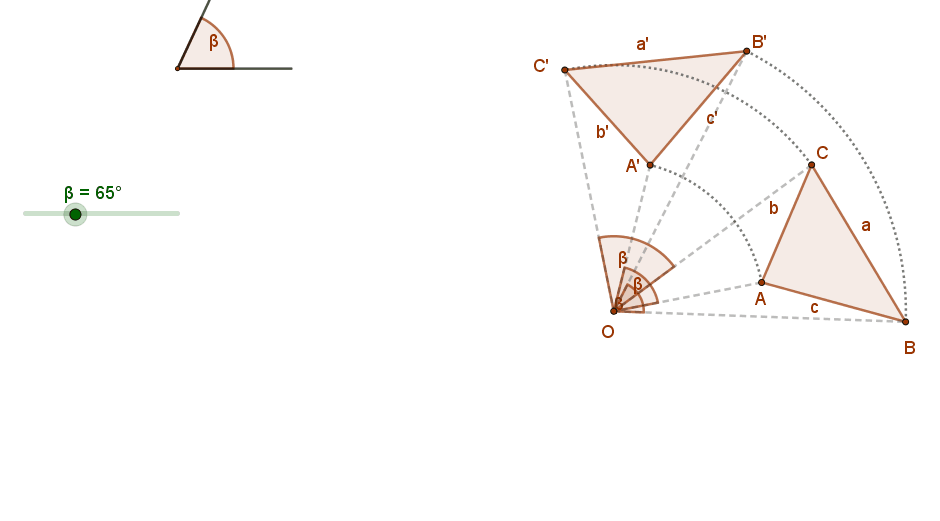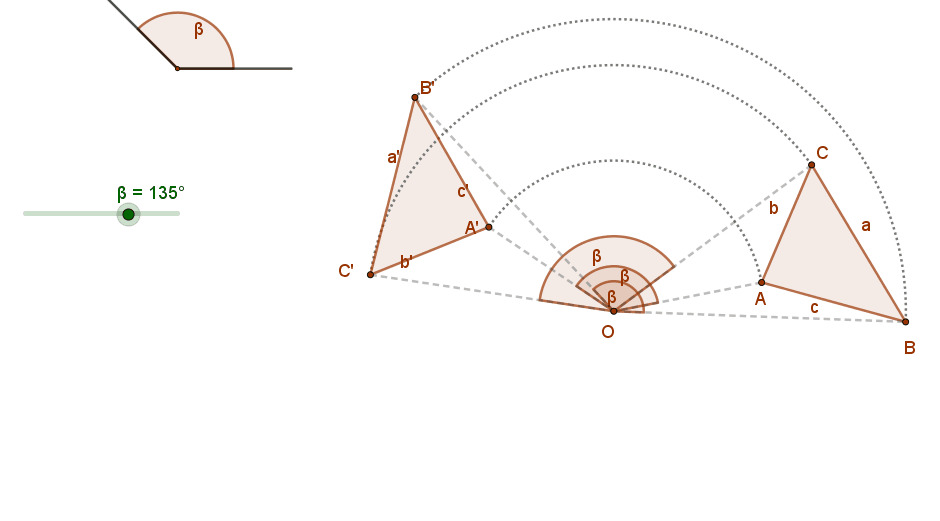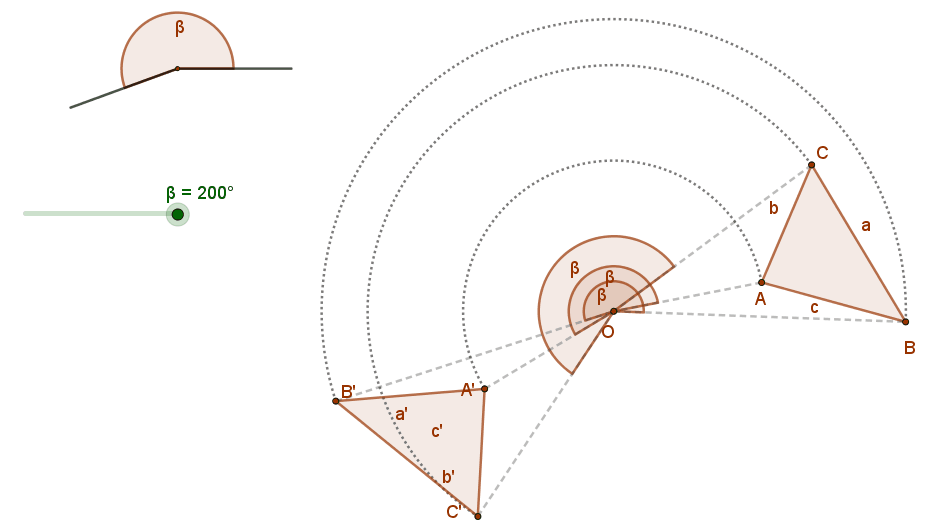
2. Távolságtartó és szögtartó. A szakasz képe vele azonos hosszúságú szakasz, szög képe vele azonos nagyságú szög. Azaz a pont körüli forgatás egybevágósági transzformáció.

3. A pont körüli forgatás irányítástartó.

4. A pont körüli forgatás az eg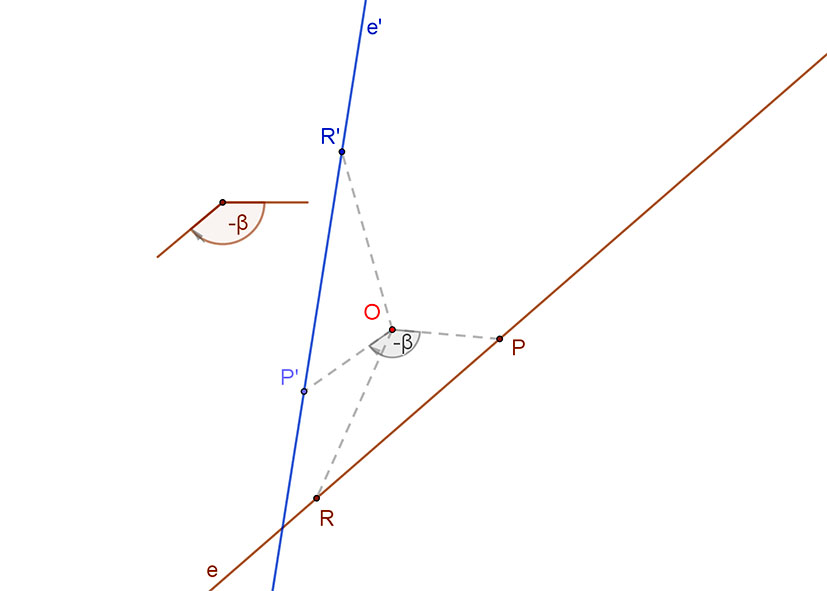yenest (e) olyan egyenesbe viszi át, amely az eredeti egyenessel a forgatás szögével (vagy annak kiegészítő szögével) megegyező szöget zár be.

 

A pont körüli forgatás egy speciális esete a középpontos tükrözés, amikor a forgatás szöge 180°.

A pont körüli forgatás alkalmazásai:

1. Szög mérése

2. Középponti szög fogalma

3. Körív hossza, körcikk területe

4. Forgásszimmetrikus alakzatok