Minden négyzet alapú egyenes gúla két (független) adattal meghatározható.
Ezek lehetnek például: alapél és gúla magasság; alapél és oldalél; alapél és oldalél-alaplap hajlásszöge; stb.
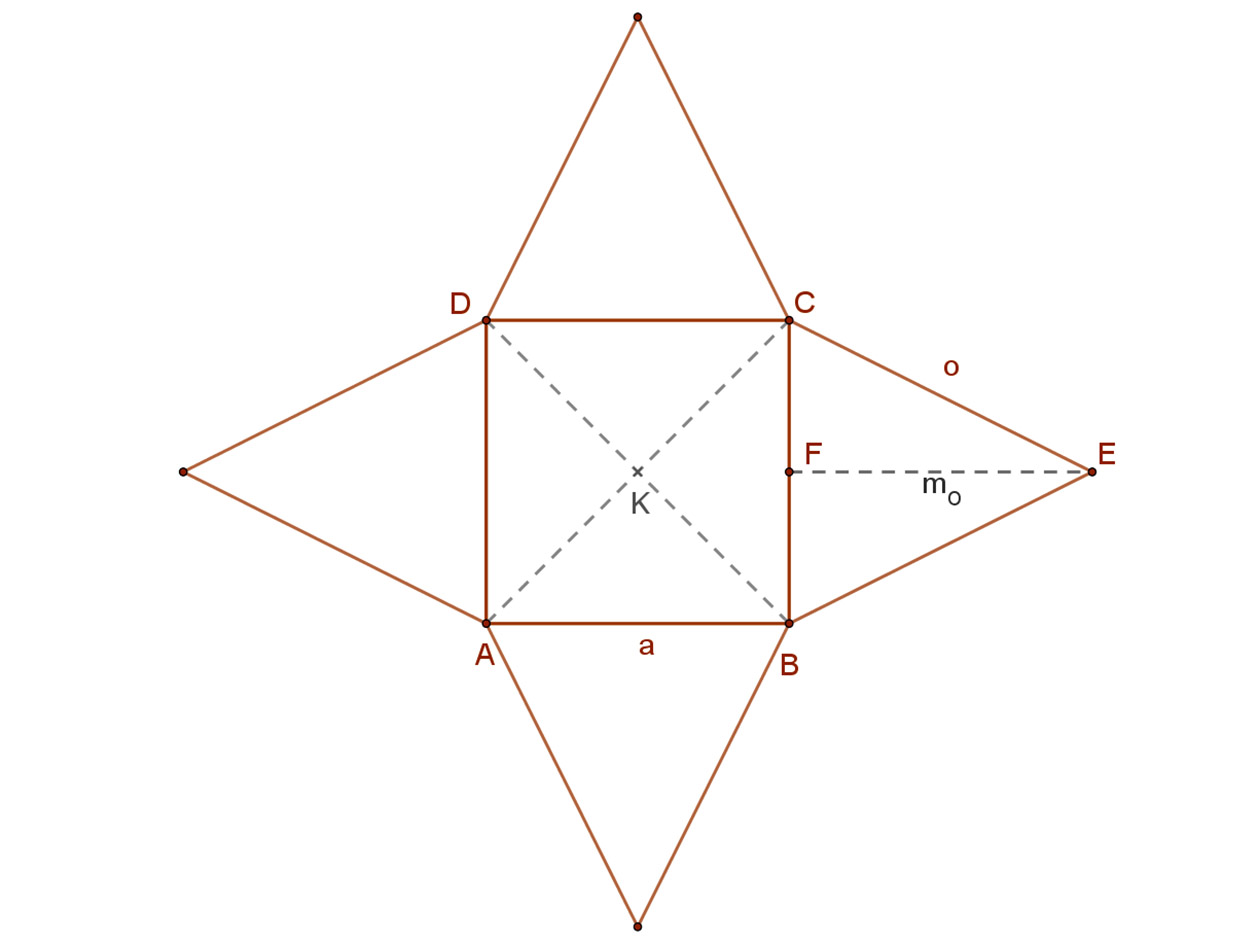
Egy négyzet alapú egyenes gúla oldallapjai egybevágó egyenlőszárú háromszögek. A gúla magassága a gúla csúcsából (E) az alaplapra bocsájtott merőleges talppontja (K) az alaplap (ABCD) négyzet középpontja.
A négyzet alapú egyenes gúlák közül talán az egyik legismertebb a gizai nagy piramis, más néven a Kheopsz piramis. Az ókori világ hét csodája közül ez az egyetlen, amely még látható.
A Kheopsz piramis méretei lenyűgözőek. Ennek négyzet alapú gúlának két meghatározó (eredeti) adata: alapélének hossza: 232.4 méter, magassága: 146.7 méter. (A mai méretek egy kicsit ettől eltérőek: kb. 230 és 137.5 méter.)
Ebből a két adatból a négyzet alapú gúla, így a piramis többi adata már kiszámolható.
Feladat:
- Számítsuk ki a Kheopsz piramist alkotó négyzetalapú gúla térfogatát és felszínét!
- Határozzuk meg az {oldalél – alapél}, az {oldalél – alaplap}, és az {oldallap – alaplap} hajlásszögét!
- Számítsuk ki a piramisba, a négyzet alapú gúlába írható gömb sugarát!
- Határozzuk meg a négyzet alapú gúla köré írt gömbjének középpontját és sugarát.
Megoldás:
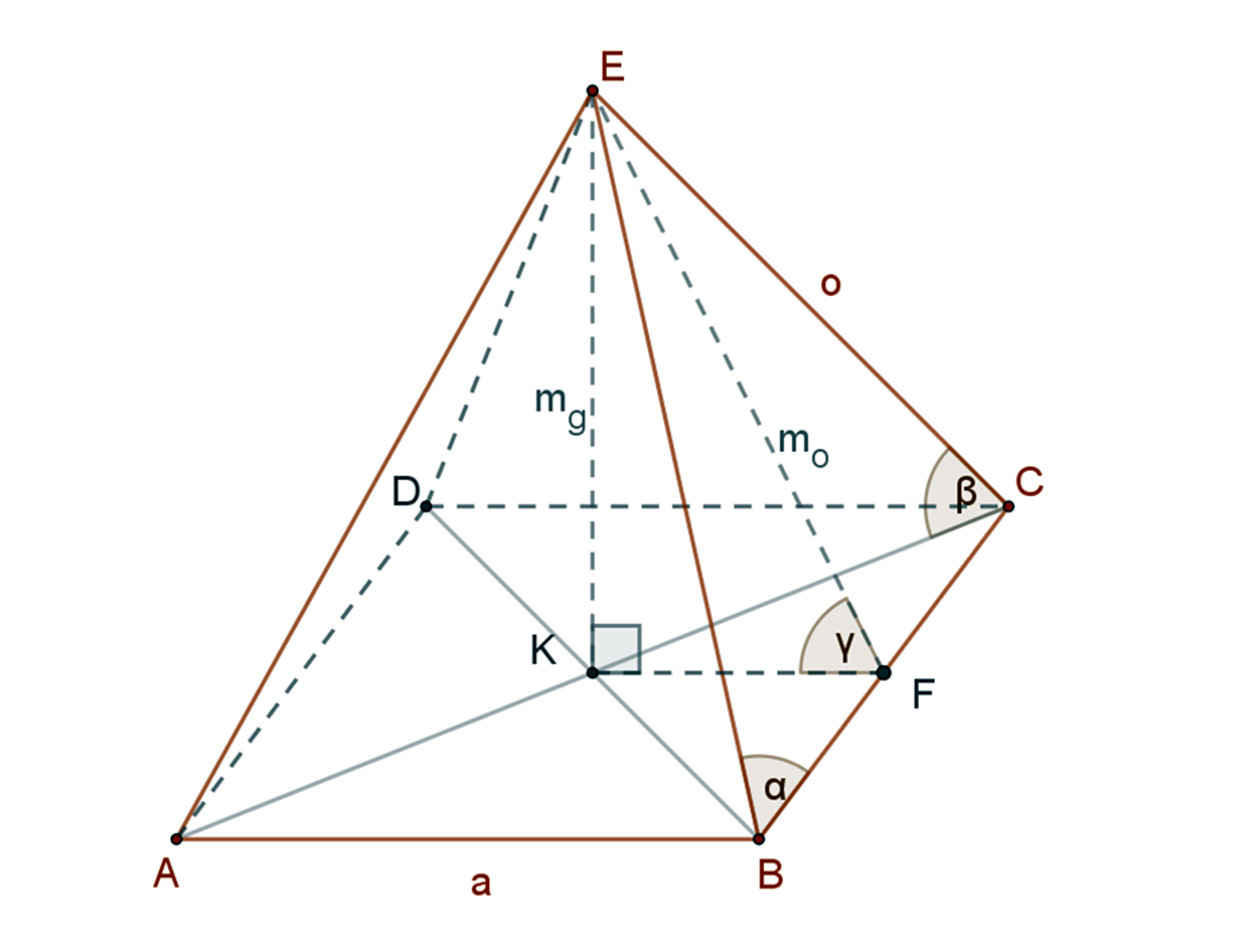Készítsük el a piramis modelljét! A mellékelt ábrán a=232.4 m és mg=146.7 m.
1.a) A gúla térfogatának a kiszámítása nagyon egyszerű. Alapterület szorozva a gúla magasságával és osztva hárommal. Képlettel: \( V_{g}=\frac{t_{a}·m_{g}}{3} \).
Az alapterület: \( t_{a}=232.4^{2}=54 009.76 \; m^{2} \).
Így a Kheopsz piramis térfogata: \( V_{g}=\frac{54009.76·146.7}{3}=\frac{7923231.792}{3}≈2 \; 641 \; 077 \; m^{3} \).
A piramis térfogata normál alakban tehát: Vg≈ 2.6⋅106 m3. Azaz kb. 2,6 millió köbméter.
1.b A gúla felszíne az alaplap területének (\( t_{a}=232.4^{2}=54 009.76 \; m^{2} \))és a 4 darab egybevágó oldallap területének az összege. Azaz: \( A_{g}=t_{a}+4·t_{o} \). Itt to az oldallap területét jelenti.
Az oldallapok egyenlőszárú háromszögek. A terület meghatározásához előbb számoljuk ki az az oldallap magasságának (mo) hosszát az FKE derékszögű háromszögből Pitagorasz tétellel: \( m_{g}^{2}+\left( \frac{a}{2} \right) ^{2}=m_{o}^{2} \).
Adatokkal: \( m_o=\sqrt{146.7^{2}+116.2^{2}}=\sqrt{21520.89+13502.44}=\sqrt{35023.33}≈187 \; m \).
Egy oldallap területe: \( t_{o}=\frac{a·m_{o}}{2} \). Adatokkal: \( t_{o}=\frac{232.4·\sqrt{35023.33}}{2}≈21746.27 \; m^{2} \).
Így a gúla felszíne: Ag≈54009.76+4⋅21746.27=54009.76+86985.09≈140 995 m2.
A piramis felszíne normál alakban tehát: Ag≈ 1.4⋅105 m2.
A gúla oldalélének hossza szintén Pitagorasz tétellel számolható például az FEC derékszögű háromszögből:
\( o≈\sqrt{116.2^{2}+187.14^{2}}≈\sqrt{13502.44+35023.33)}=\sqrt{48525.77}≈220.3 \; m \).
2. A hajlásszögek meghatározása. Ezeknek a kiszámításához a hegyesszögek szögfüggvényeinek ismeretére is szükség van. A következőkben a Kheopsz piramisra vonatkozó számítások láthatók.
2.a) Oldalél és alapél hajlásszöge (α).
A BFE derékszögű háromszögben: \( tg(α)=\frac{m_{o}}{a/2} \). Tehát: \( tg(α)≈\frac{187.15}{116.2}≈1.61. \). Így α≈ 58.2°.
2.b) Oldalél és alaplap hajlásszöge (β).
A CKE derékszögű háromszögben: \( sin(β)=\frac{m_{g}}{o} \).
Tehát: \( sin(β)≈\frac{146.7}{220.3}≈0.6659 \). Így β≈41.8°.
2.c Oldallap és alaplap hajlásszöge (γ).
Az FKE derékszögű háromszögben: \( cos(γ)=\frac{a/2}{m_{o}} \).
Tehát: \( cos(γ=\frac{116.2}{187.14}≈0.6909 \). Így γ≈51.6°.
3. Beírt gömb.
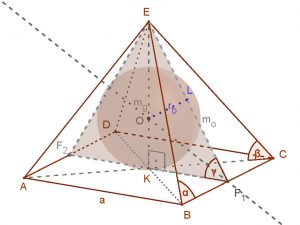A négyzet alapú gúlába írt gömb a gúla minden lapját (alaplapját és a négy oldallapját is) érinti. Ennek a gömbnek a főköre beírt köre annak az egyenlőszárú háromszögnek, amelynek oldalai az alaplap középvonala és két szemben lévő oldallap magassága. A mellékelt ábrán ez az F2F1E háromszög. A beírt gömb középpontja tehát a test magasságán (szimmetria-tengelyén) van. A háromszögbe írt kör (O) középpontját ennek az(F2F1E) háromszögnek a szögfelezői metszik ki. A beírt kör sugarát megkapjuk, ha ebből az O pontból merőlegest állítunk az oldallap magasságára. Így kapjuk az L pontot.
A beírt kör (OL) sugarának hosszát kiszámíthatjuk ennek a háromszögnek a segítségével a tF2F1E=rb⋅s képlet segítségével. Itt „s” a háromszög kerületének a fele.
A Kheopsz piramis esetén a beírt gömb sugarát tehát a következő számítás adja:
\( t_{LFE}=\frac{232.4·146.7}{2}≈17046.54 \; m \). Az F2F1E háromszög kerülete: a+2⋅mo. Azaz 232,4 +2⋅187 m. Így s= 303.3 m.
Tehát a Kheopsz piramis oldallapjait érintő gömb sugara rb≈56.2 m lenne.
Megjegyzés: Ha egy poliéderbe (sokszöglapokkal határolt test) gömb írható, akkor ennek a gömbnek a sugarát a következő összefüggéssel is megkaphatjuk: \( r_{b}=\frac{3·V}{A} \). Azaz a térfogat háromszorosát osztjuk a felszín mértékével.
A Kheopsz piramis esetén: \( r_{b}=\frac{3·2641077}{140995}≈56.2 \)m.
Persze nem minden poliéderbe írható gömb. Hiszen a például a téglatestbe sem, ha az nem kocka.
4. Köré írt gömb.
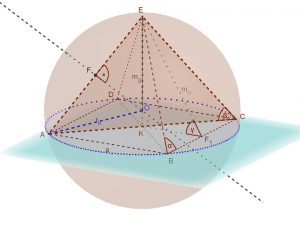A négyzet alapú gúla köré írt gömb (O) középpontja egyenlő távol van a gúla (ABCDE) csúcsaitól. Mivel az mg magasságvonal minden pontja egyenlő távol van az alaplap négy csúcsától, tehát ez az (O) pont illeszkedik a magasságvonalra. Az (O) pontot megkapjuk, ha az ACE átlós sík által kimetszett (ACE) egyenlőszárú háromszögben megszerkesztjük az AE szakasz oldalfelező merőlegesét. Ez metszi ki a magasságvonalon a köré írt gömb (O) középpontját.
A köré írt kör rk sugarának hosszát a következőképpen számolhatjuk ki:
Az AKE és az OFE derékszögű háromszögek hasonlóak, hiszen van még egy közös szögük (AEK) is. Írjuk fel az oldalak arányát: EO:EF=EA:EK.
Itt EO=AO=rk a köré írt gömb sugara, a AE: a gúla (o) oldaléle, EF az oldalél fele, EK pedig a gúla mg magassága.
Tehát rk:o/2=o:mg, vagyis \( r_{k}=\frac{o·o/2}{m_{g}} \).
A Kheopsz piramis esetén: \( r_{k}=\frac{220.3·110.15}{146.7}≈165.41 \)m.
Megjegyzés:A mellékelt ábrától eltérően ebben az esetben az rk>mg. Ez azt is jelenti, hogy a gömb kör írt középpontja a Kheopsz piramis esetében a gúlán kívül lenne. A piramis két átellenes oldaléle tompa szöget (AEC∠: 180°-2⋅β)=180°-2⋅41.8°=96.4°) zár be.
