Egyenes – sík illetve két sík hajlásszöge

Egyenes és sík illetve két sík hajlásszögének meghatározásánál induljunk ki a térelemek kölcsönös helyzetéből.

A) Egyenes és sík hajlásszöge

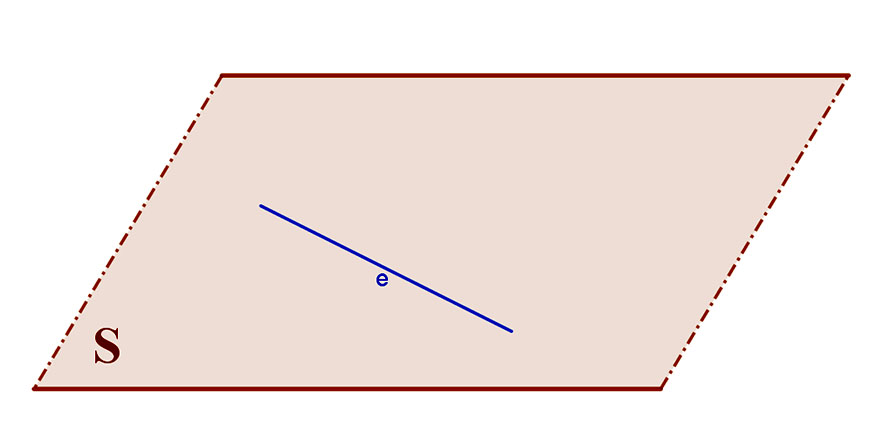
1.  Egyenes illeszkedik a síkra.

Ekkor hajlásszögük 0°.

 

2. Az egyenes párhuzamos a síkkal.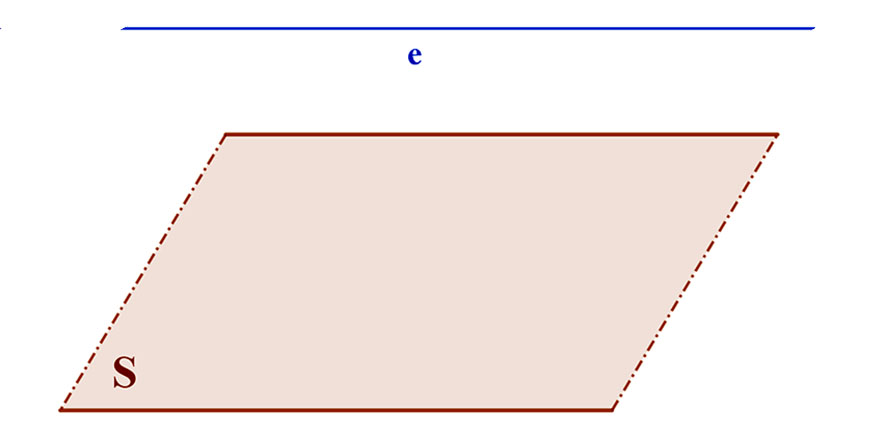

Az egyenes és sík hajlásszöge ebben az esetben is 0°.

 

 

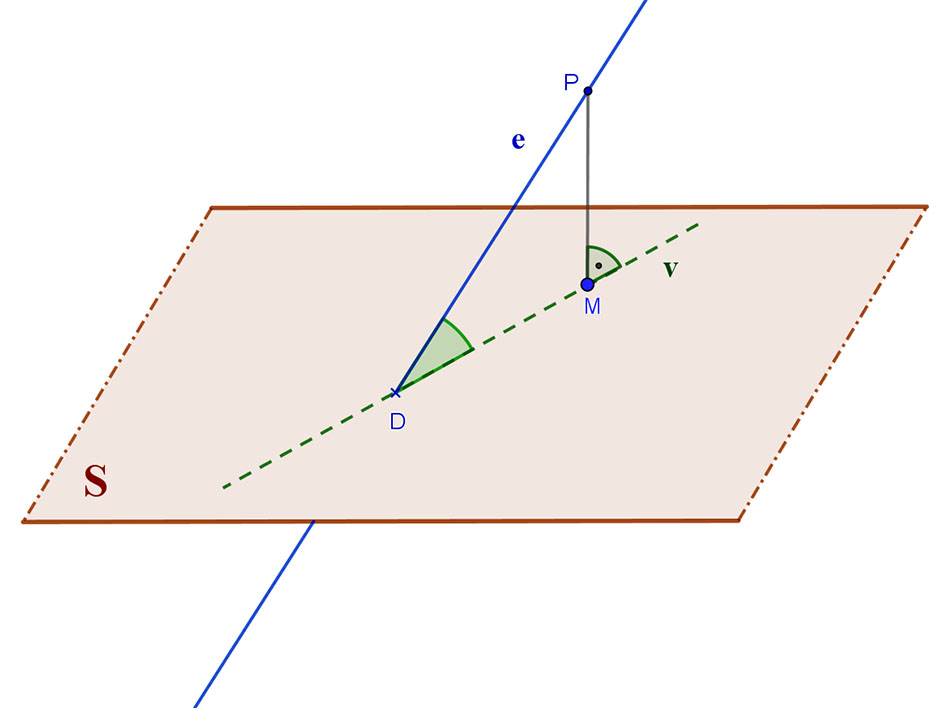3. Az „e” egyenes döfi a síkot (D pontban), de nem merőleges rá.

Bocsássunk az egyenes egy tetszőleges síkon kívüli P pontjából merőlegest a síkra, így kapjuk a M pontot. A DM pontokon áthaladó „v” egyenes az „e” egyenesnek a síkra vonatkozó merőleges vetülete.
Az „e” egyenes és az „S” sík hajlásszöge az egyenesnek és merőleges vetületének hajlásszögével egyenlő.

 

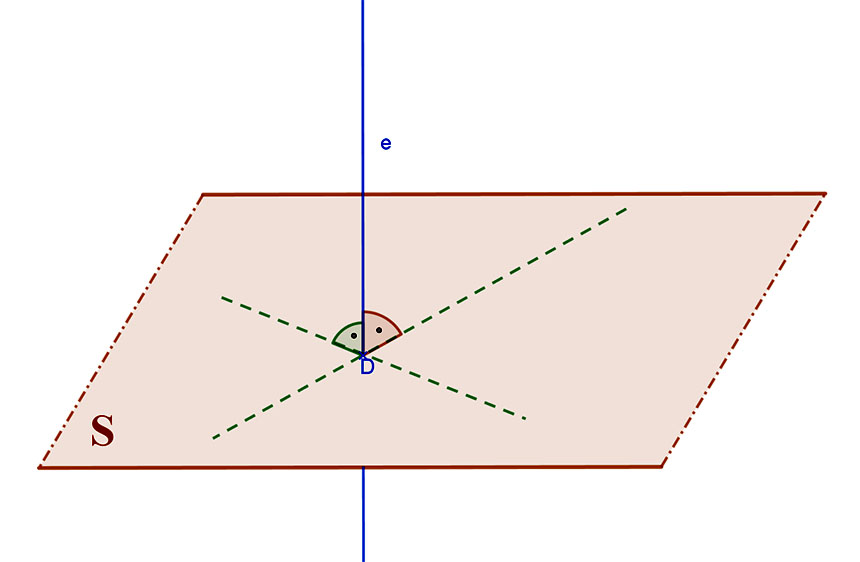4. Az egyenes merőleges a síkra.

Egy egyenes és egy sík akkor merőleges egymásra, ha az egyenes merőleges a sík minden egyenesére. Az egyenes és a sík hajlásszöge ebben az esetben 90°.

Tétel:

Ha egy egyenes merőleges a sík két egymást metsző egyenesére, akkor merőleges a sík minden egyenesére, azaz merőleges síkra.

B) Két sík hajlásszöge

1. Két sík illeszkedik egymásra.

Ekkor hajlásszögük 0°.

 

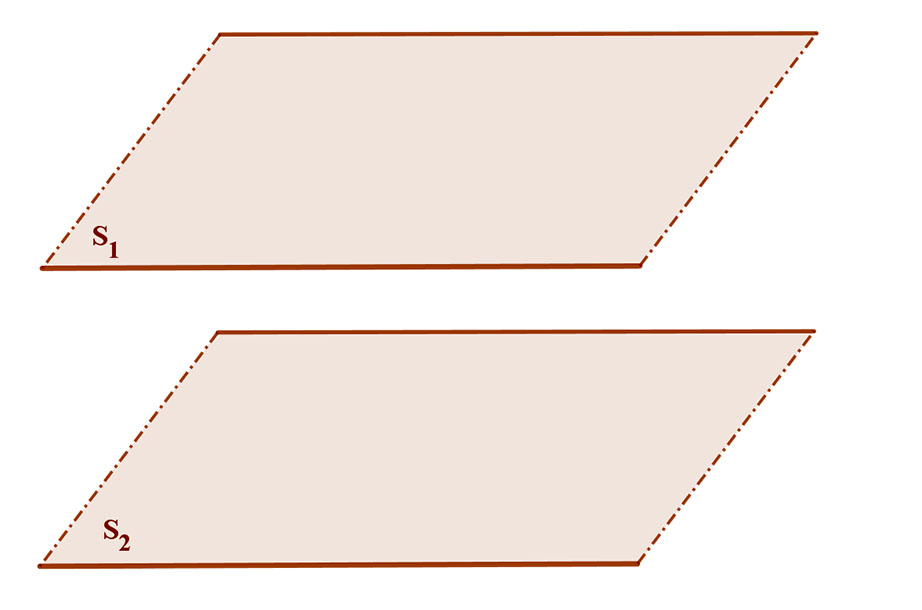2. Két sík nem illeszkedik egymásra, de párhuzamos egymással.

Két sík hajlásszöge ebben az esetben is 0°.

 

 

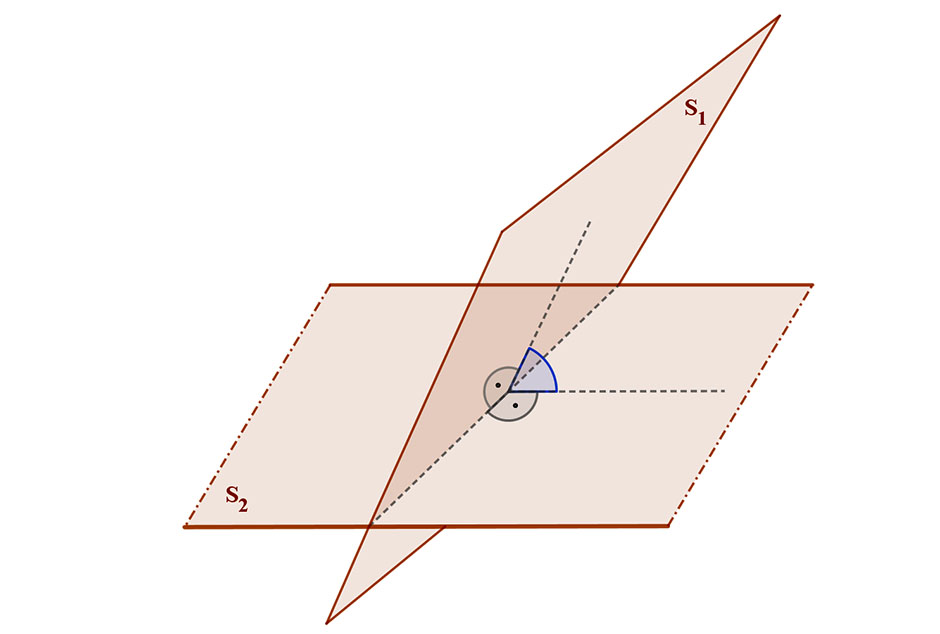3. Két sík metszi egymást.

A két sík metszésvonalának tetszőleges pontjában a két sík mindegyikén belül merőlegest állítunk a metszésvonalra. Két metsző sík hajlásszögén az így kapott két egyenes hajlásszögét értjük.