1. A legismertebbek az un. közepek között fennálló egyenlőtlenségek:
Harmonikus közép≤Számtani közép≤Mértani (Geometriai) közép≤Négyzetes közép.
Formulával (két nem-negatív) valós szám esetén):
H(a;b)≤G(a;b)≤A(a;b)≤N(a;b), ahol a;b∈ℝ; a≥0; b≥0.
Ezeket az egyenlőtlenségeket értelmezhetjük nemcsak két, hanem több valós számra is.
A közöttük fennálló egyenlőtlenségek igazolását itt találhatjuk.
2. Az alábbi egyenlőtlenség a következőképpen szól:
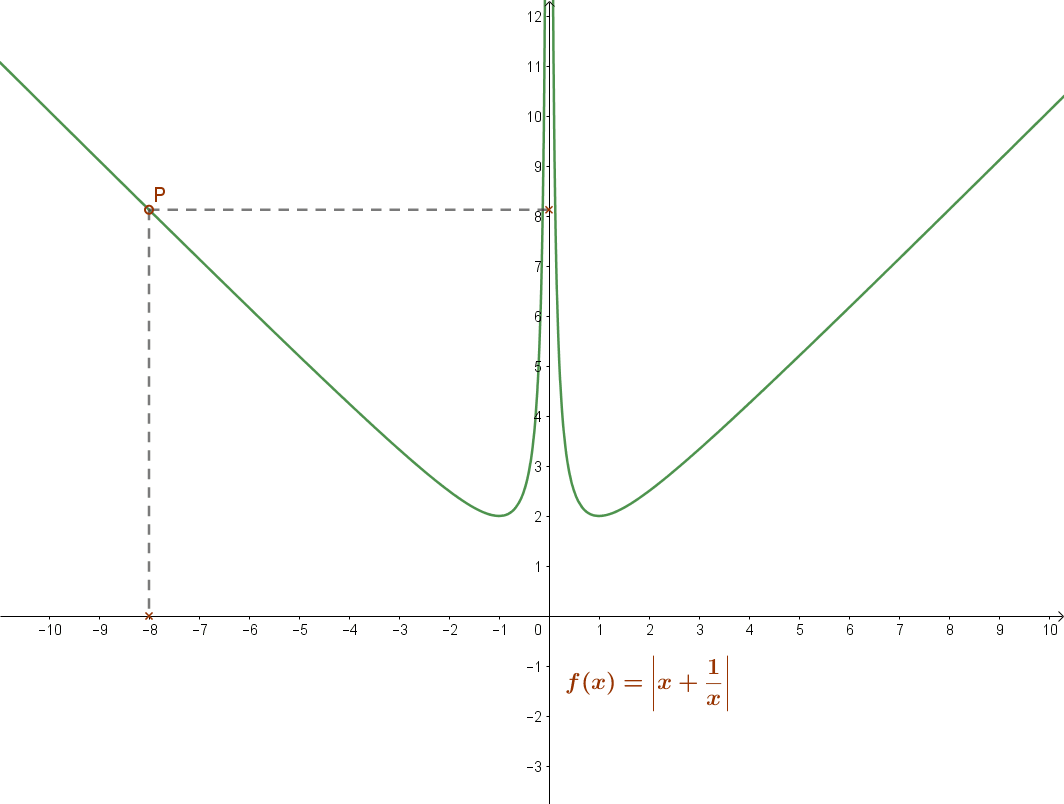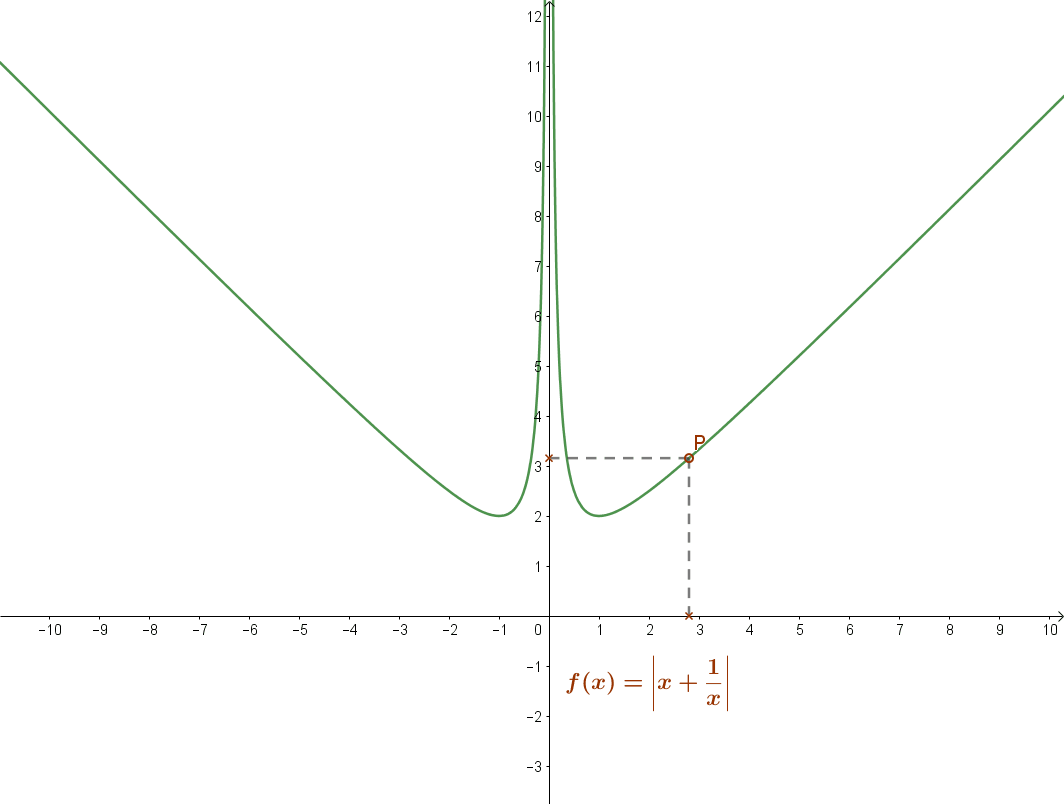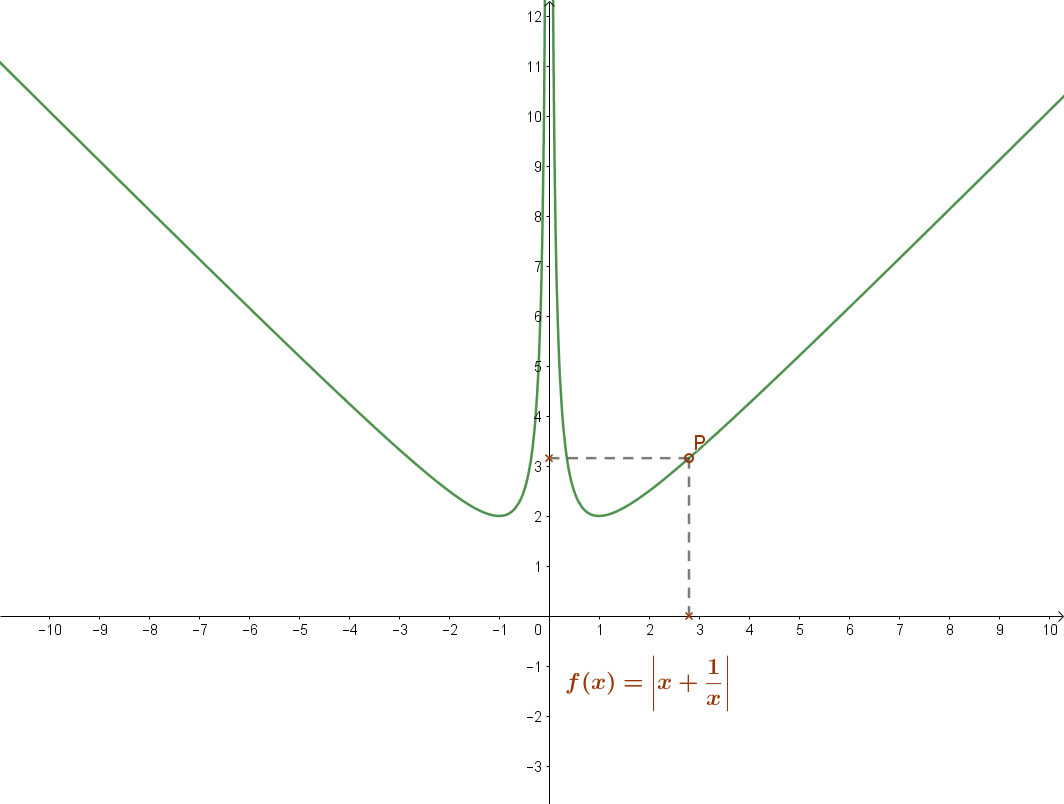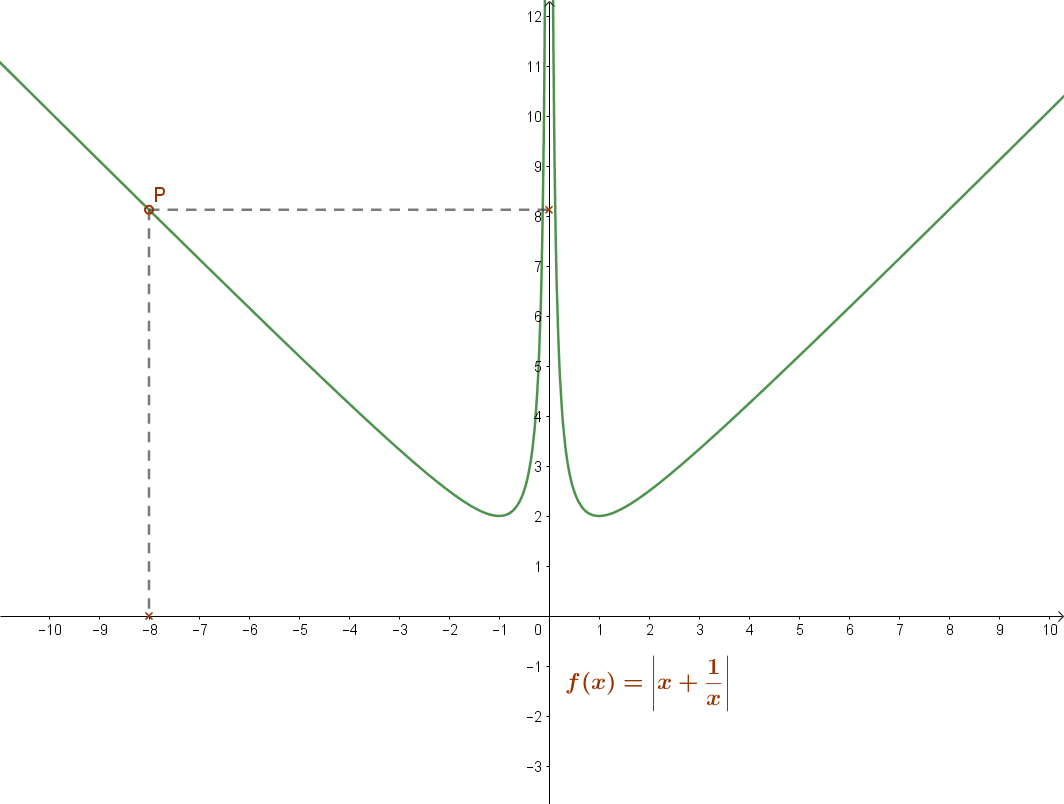
Bármely nullától eltérő valós szám és reciproka összegének abszolút értéke nem kisebb kettőnél.
Formulával: \( \left|a+\frac{1}{a} \right| ≥2 \; a∈\mathbb{R} \; a≠0 \).
Bizonyítás:
a) Pozitív valós szám esetén a>0 az abszolút értéknek nincs szerepe, így a bizonyítandó állítás: \( a+\frac{1}{a}≥2 \).
A zárójel felbontása után „a”-val átszorozva: a2+1≥2a.
0-ra redukálva: a2-2a+1≥0.
A bal oldal teljes négyzet, így az állítás igaz. (a-1)2≥0.
b) Negatív valós szám esetén (a<0)
Ebben az esetben az abszolút értékben szereplő kifejezés ellentettjét kell venni: \( -\left(a+\frac{1}{a}\right)≥2 \).
Bontsuk fel a zárójelet: \( -a-\frac{1}{a}≥2 \)
Szorozzunk át a negatív változóval „a”-val. Mivel negatív értékkel szoroztunk, a relációs jel megfordul:
-a2-1≤2a.
0-ra redukálva: -a2-2a-1≤0
-1-gyel átszorozva, a relációs jel újra fordul: a2+2a+1≥0.
A bal oldal teljes négyzet, így az állítás igaz. (a+1)2≥0.
Azt kaptuk tehát, hogy az állítás mindkét esetben igaz.
Függvényként ábrázolva: \( f(x)=\left|x+\frac{1}{x}\right| \).
3. Bernoulli-egyenlőtlenség: (1+a)n≥1+n⋅a; a∈ℝ; a>-1; n∈ℕ.
(Az a>-1 feltétel biztosítja, hogy az (1+a)n kifejezésben a hatvány alapja pozitív legyen.)
Bizonyítás teljes indukcióval:
a) n=1 esetén: (1+a)1=1+1⋅a.
n=2 esetén: (1+a)2=1+2⋅a+a2≥1+2a.
b) Az indukciós feltevés: „n”-re még igaz: (1+a)n≥1+n⋅a.
c) Bizonyítandó n+1-re: (1+a)n+1≥1+(n+1)⋅a.
Hatványozás azonosságával: (1+a)n+1=(1+a)n⋅(1+a).
Az indukciós feltétel felhasználásával az egyenlőtlenség bal oldala: (1+a)n+1=(1+a)n⋅(1+a)≥(1+n⋅a)⋅(1+a).
Itt a jobb oldalon a beszorzást elvégezve: (1+n⋅a)⋅(1+a)=1+a+n⋅a+n⋅a2.
Kiemeléssel: (1+n⋅a)⋅(1+a)=1+a+n⋅a+n⋅a2=1+(n+1)⋅a+n⋅a2.
Tehát a bizonyítandó állításra ezt kaptuk: hogy (1+a)n+1≥1+(n+1)⋅a+n⋅a2.
Itt a jobb oldalon nem-negatív n⋅a2 tag elhagyásával a bizonyítandó állítást kapjuk:
(1+a)n+1≥1+(n+1)⋅a.


1 hozzászólás
Comments are closed, but trackbacks and pingbacks are open.