Differenciálható függvények vizsgálata

Egy differenciálható  f(x) függvény  f'(x) deriváltfüggvénye  egy adott pontban az  f(x) függvényhez az adott pontban húzható érintő meredekségét (iránytangensét) adja.

Egy differenciálható függvény jellemzését a derivált függvény a következő szempontok vizsgálatánál segíti:

1. A függvény menete.
2. A függvény szélsőértéke (szélsőértékei).
3. A függvény görbülete (Konvex, konkáv).
4. A függvény inflexiós pontja (pontjai).

1. Függvény menete és a derivált függvénye

Bevezető feladat:

Írjuk fel annak a másodfokú függvénynek az általános alakját, amelynek meredeksége 0.5 és zérushelyei: x₁=1 és x₂=5! Képezzük a függvény derivált függvényét! 

Megoldás: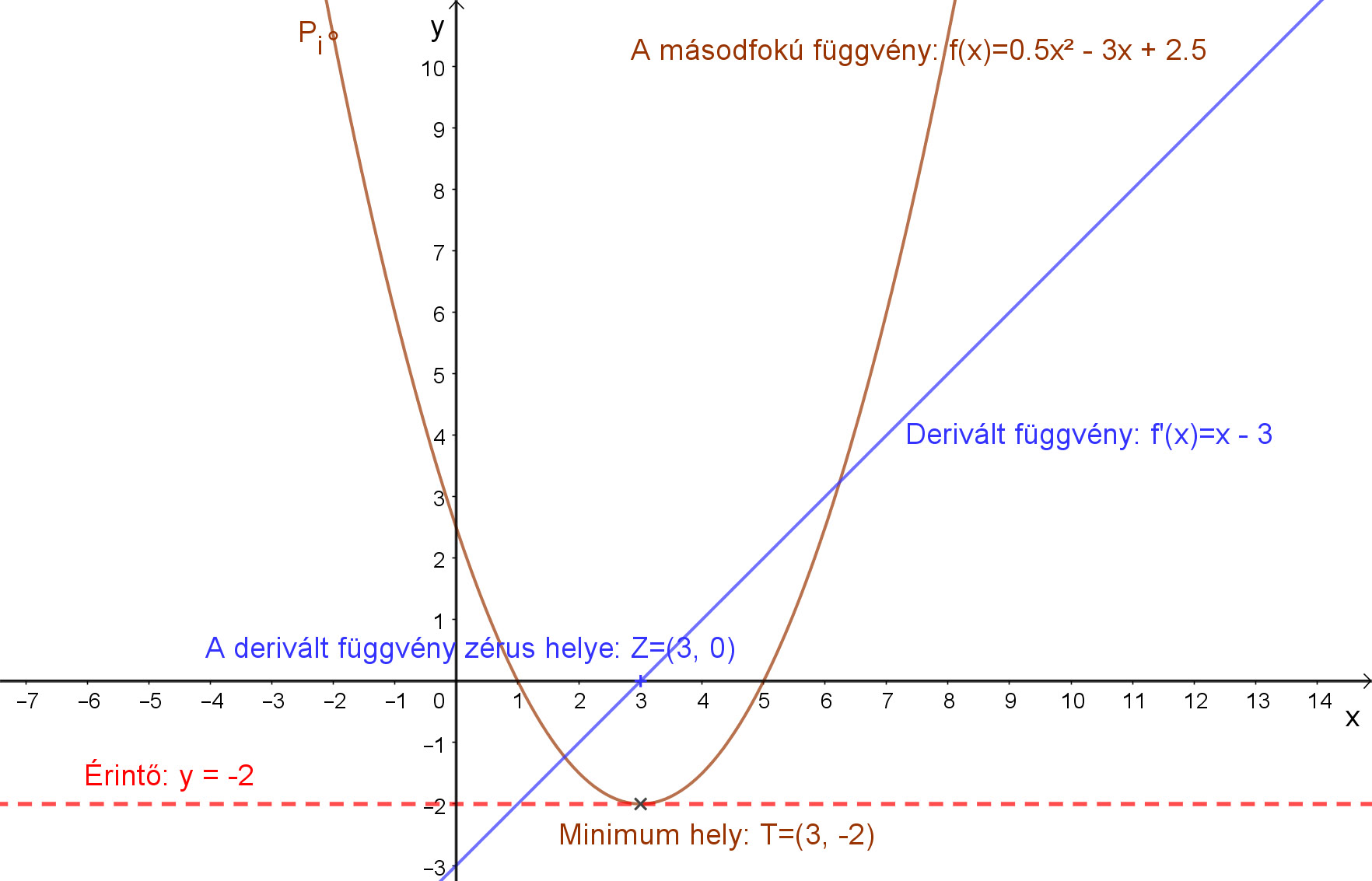

A másodfokú egyenlet gyöktényezés alakjának segítségével:
m(x)=0.5(x-1)(x-5)=0.5x²-3x+2,5= 0.5(x-3)²-2!

Az f(x)=0.5x²-3x+2,5 függvény derivált függvénye a hatványfüggvények deriválási szabálya szerint: m’(x)=x-3.

Húzzunk érintőt a függvényhez az x_i= -2; -1; 0; 1; 2; 3; 4; 7 pontokba.  Figyeljük meg az érintők meredekségeit!

Az érintők meredekségét a derivált függvény adja: m_i=m'(x_i)
Az érintő egyenlete: y-y_i=m_i(x-x_i), ahol az egyes érintési pontok:P_i(x_i,y_i).

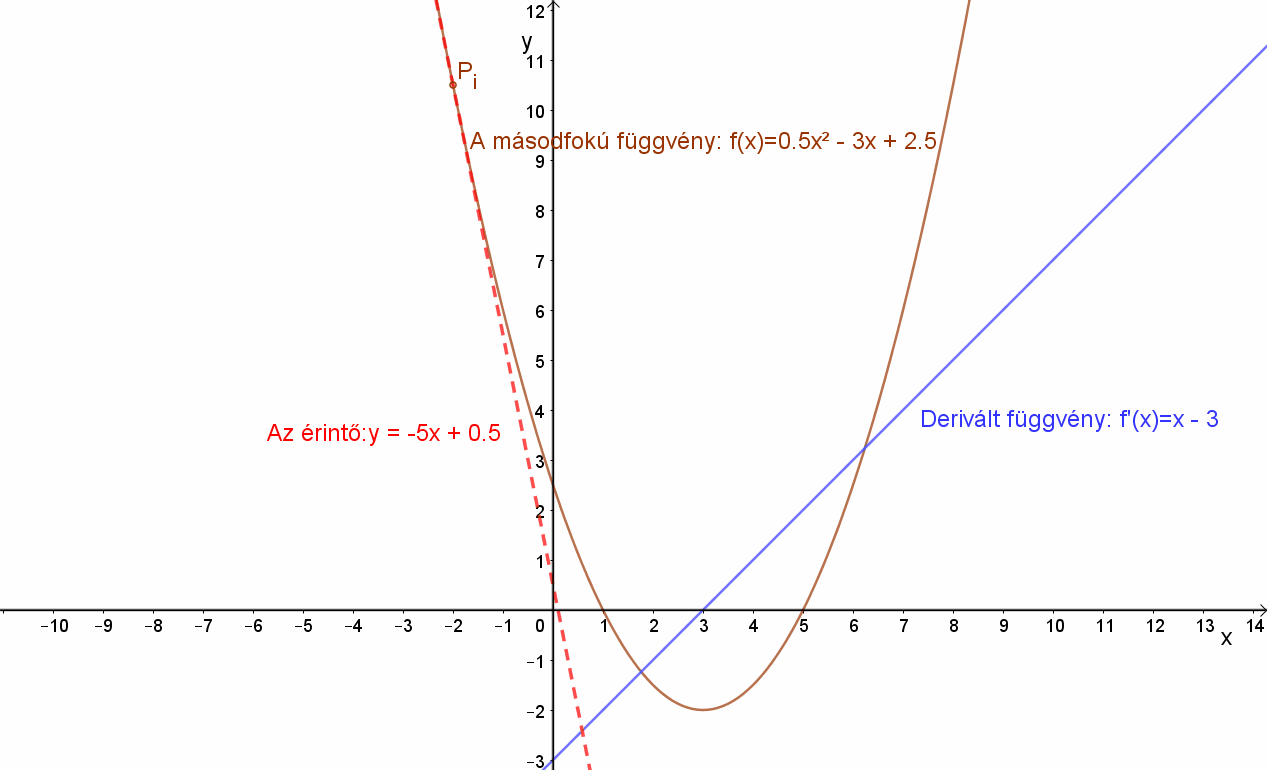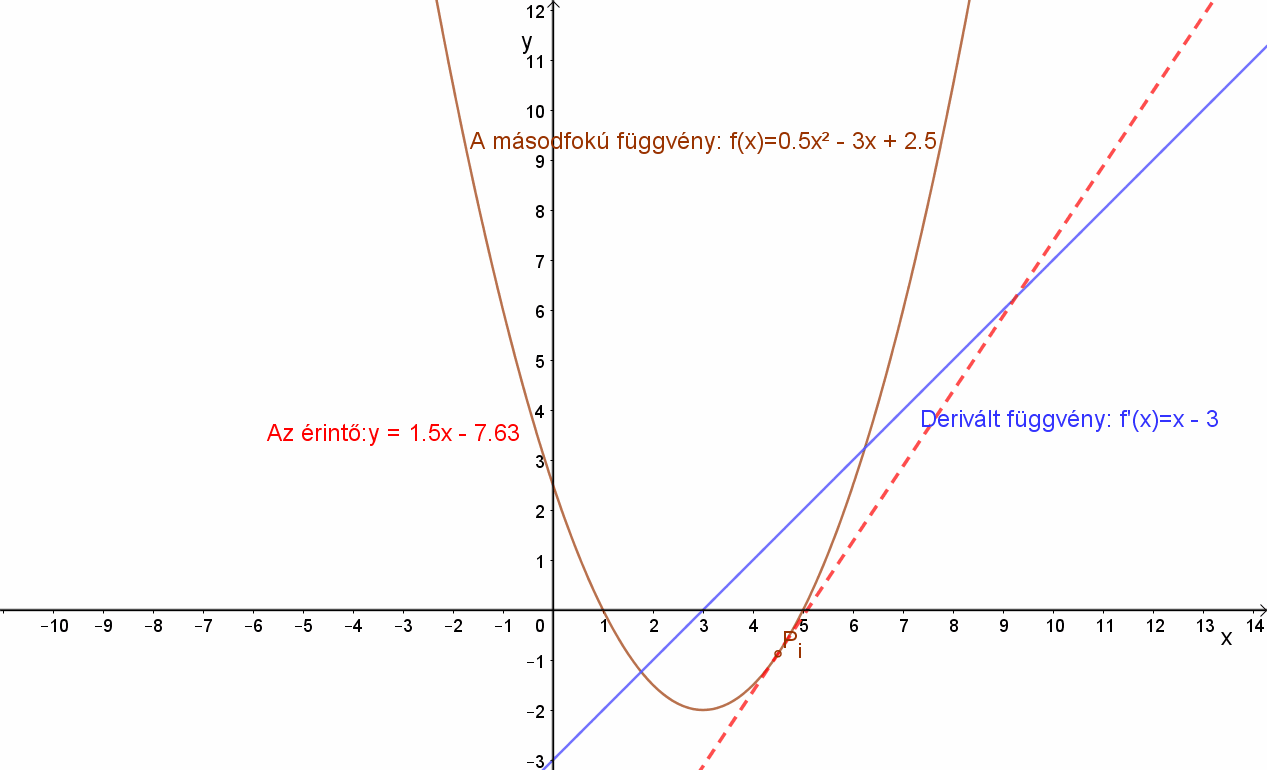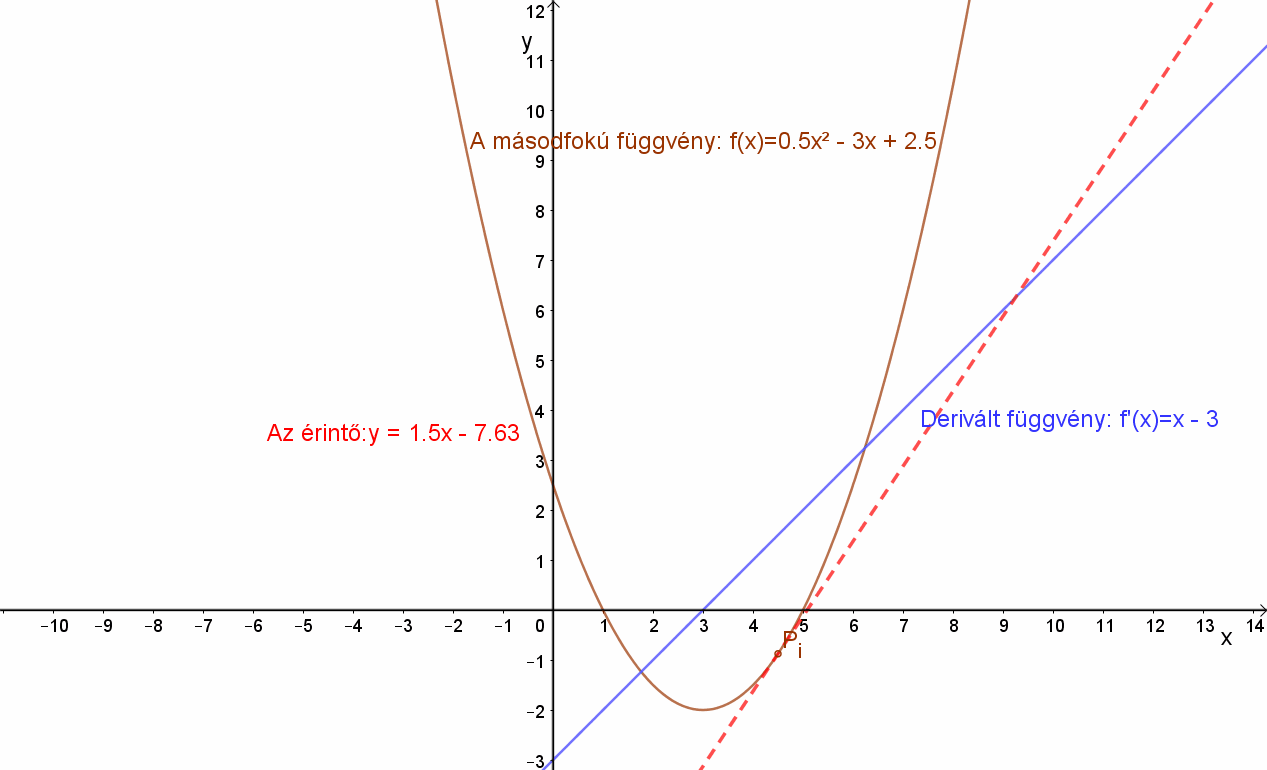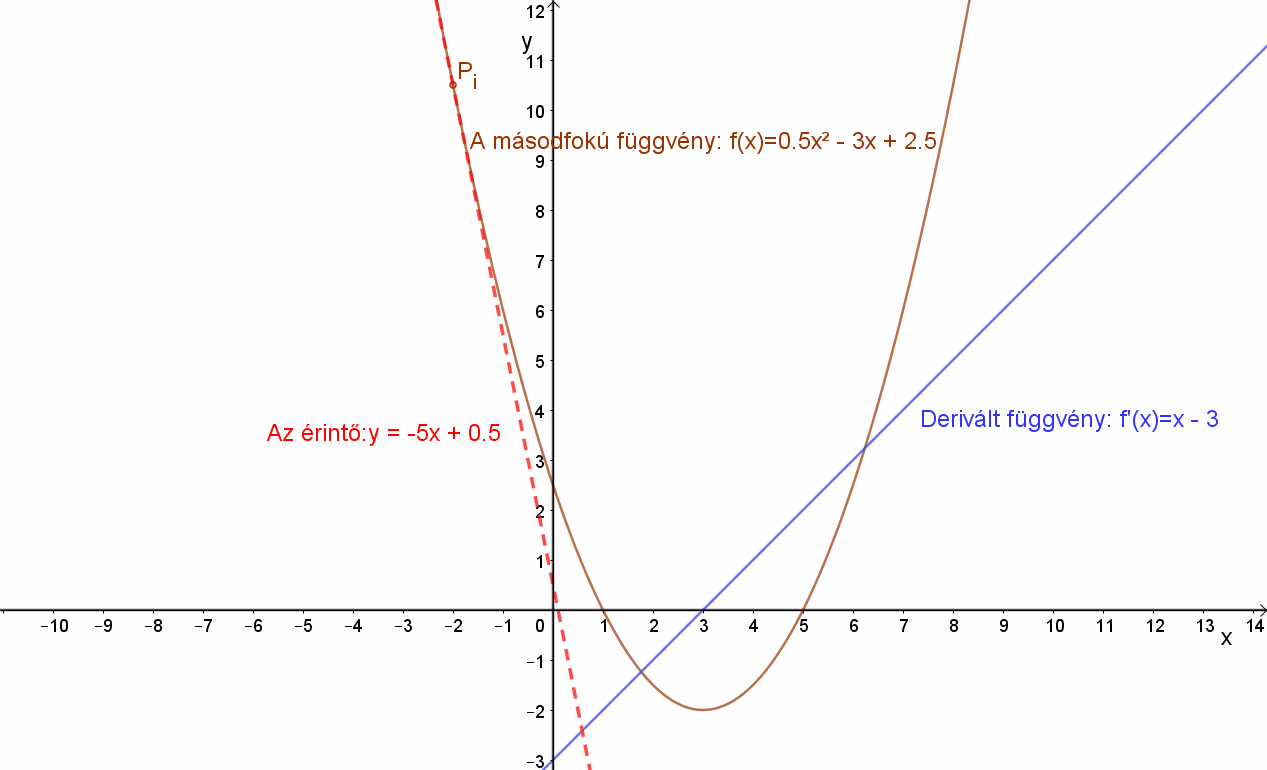
xi	-2	-1	0	1	2	3	4	7	8
Érintő meredeksége mi:	-5	-4	-3	-2	-1	0	1	4	5

Megfigyelhető, hogy a másodfokú függvény szigorúan monoton csökken, ha az érintő meredekség<0 és szigorúan monoton nő, ha az érintő meredeksége >0.

Általában is igaz:

Tétel:

Ha az (a; b) nyílt intervallumban differenciálható f(x) függvény az intervallumban monoton nő, akkor a deriváltja f’(x) az intervallum minden pontjában nemnegatív. (≥0)

Ha az (a; b) nyílt intervallumban differenciálható f(x) függvény az intervallumban monoton csökken, akkor a deriváltja f’(x)az intervallum minden pontjában nempozitív. (≤ 0)

Bebizonyítható a fenti állítások megfordítása is:

Tétel:

Ha az f’(x) derivált függvény az (a; b) nyílt intervallumban nemnegatív (nempozitív), akkor az f(x) függvény monoton növekvő (csökkenő).

Megjegyzés:

A függvény szigorú monotonitásából csak az következik, hogy a derivált függvény ≥0 illetve ≤ 0.
Például az f(x) = x³ függvény mindenütt szigorúan monoton nő, de az x_i = 0 ponton a derivált értéke = 0.

2. Függvény szélsőértéke és derivált függvénye kapcsolata

A függvény vizsgálatokban kitüntetett szerepe van a szélsőértékek létezésének és elemzésének vizsgálatának.
A szélsőérték fogalmát érdemes lokális (helyi) értelemben, azaz egy nyílt intervallumon értelmezni és vizsgálni.

Példa:

A fenti f(x)=0.5x²-3x+2,5  másodfokú függvény grafikonja egy parabola. Ennek függvénynek minimuma van a T(3,-2) pontban. Ebben a pontban a parabolához húzott érintő egyenlet: y=-2. Ez egy, az „x” tengellyel párhuzamos egyenes, amelynek meredeksége nulla.

Ez a pont a derivált függvény zérus helye.

Tétel:

Az (a; b) nyílt intervallumban differenciálható f(x) függvénynek az intervallum x₀ pontjában csak akkor lehet lokális szélsőértéke, ha ott f’(x₀)=0.
Ez a szélsőérték létezésének szükséges, de nem elégséges feltétele.

Ugyanakkor az f(x) = x³ hatvány függvénynek sehol sincsen szélsőértéke, a függvény szigorúan monoton nő, mégis, van olyan pontja, ahol a derivált = 0, ahol az érintő párhuzamos az „x” tengellyel.

Tehát a derivált nulla voltából nem következik a szélsőérték létezése, de ahol (lokális) szélsőérték van, ott a derivált biztosan nulla.

Ha emellett az f’ derivált függvény ennek a pontnak a környezetében előjelet is vált, akkor az f(x) függvénynek ebben az x₀ pontban lokális szélsőértéke van.

Megjegyzés:

A derivált adott pontban való zérusértéke és előjelváltása elégséges, de nem szükséges feltétele a szélsőérték létezésének. Van olyan függvény, amelynek egy adott pontjában van lokális szélsőértéke, de a derivált függvény ennek pontnak a környezetében nem vált előjelet.

Feladat:

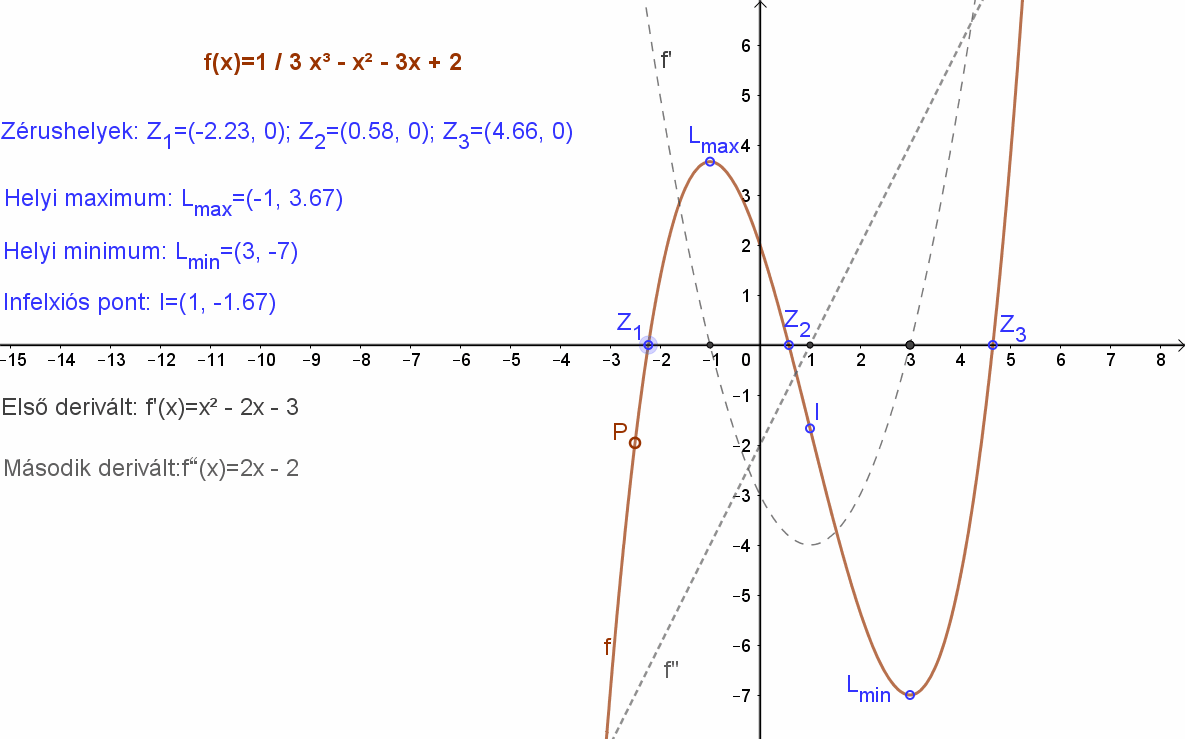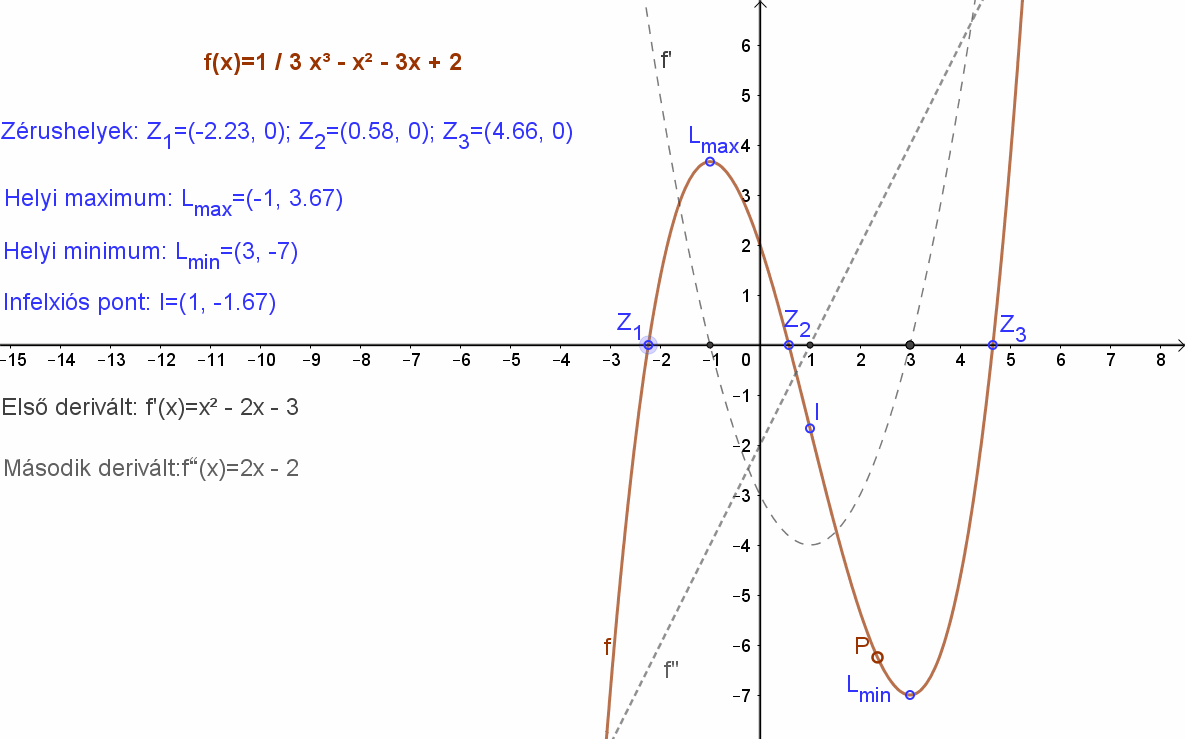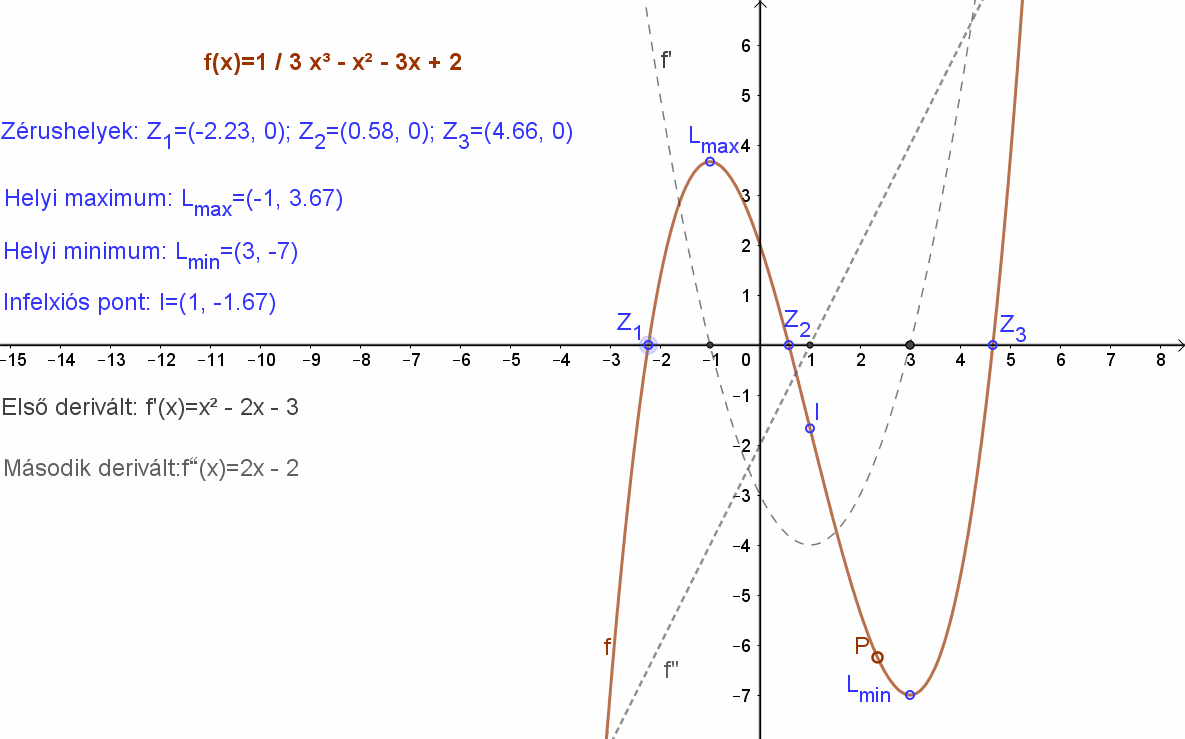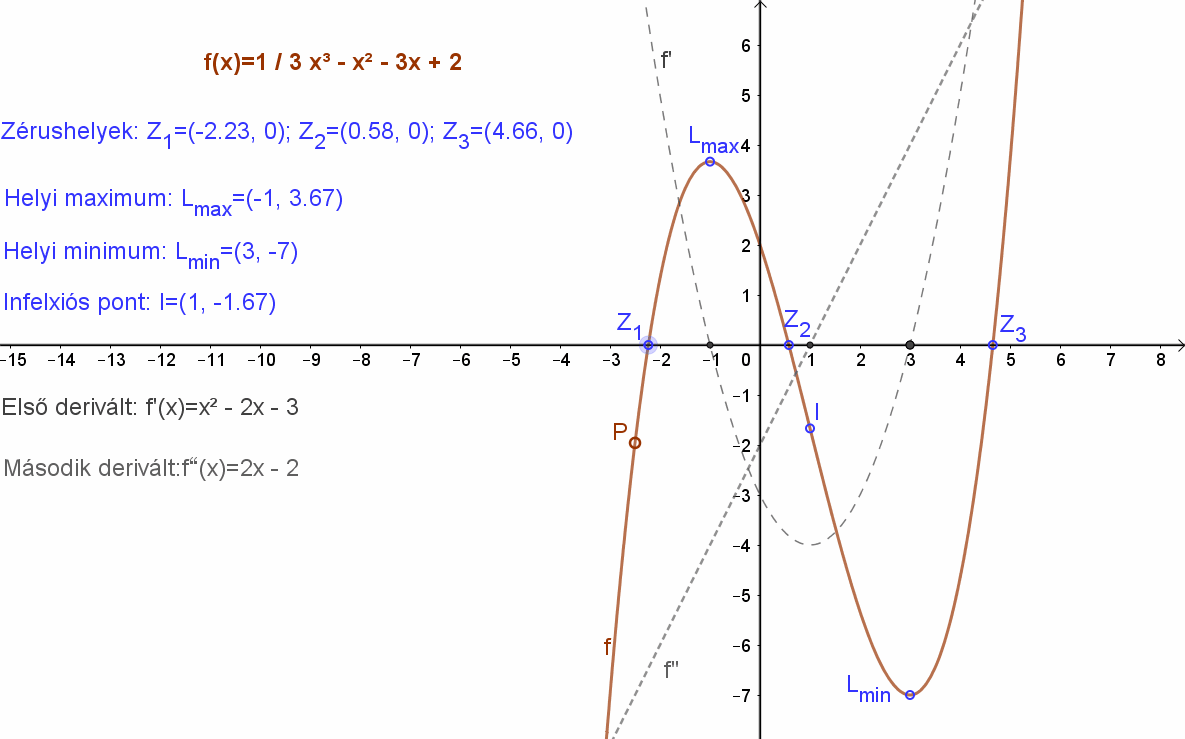
Elemezzük az ​\( f(x)=\frac{1}{3}·x^3-x^2-3x+2 \)​ függvényt monotonitás és szélsőérték szempontjából!  

Az nyilvánvaló, hogy a függvény a (0,2) pontban metszi az „y” tengelyt. f(0) = 2.

Próbáljuk a derivált függvény segítségével meghatározni az eredeti függvény menetét, lokális szélsőértékeit! (típusát, helyét, értékét).
A függvényvizsgálatot tehát kezdjük avval, hogy képezzük az f(x) függvény f’(x) deriváltját függvényét! ​\( f'(x)=x^2-2x-3 \)​.
Ennek zérushelyei: f’(-1) = 0, és f’(3) = 0. Itt lehetséges az eredeti f(x) függvény lokális szélsőértéke.

Mivel a derivált függvény egy másodfokú függvény amelynek a grafikonja parabola, ezért a zérus helyeknél előjelet vált, ebből következik, hogy ezekben a pontokban a függvénynek szélsőértéke van: f(-1)=14/3, és f(3)=-7

Ha x < -1; akkor f’(x)>0, tehát itt az f(x) függvény szigorúan monoton nő, ha -1<x<3, akkor f’(x)<0, tehát a függvény ebben az intervallumban szigorúan monoton csökken. Ebből következik, hogy x = -1 helyen lokális maximuma van. Viszont, ha x>3, akkor az f’(x)>0, azaz az f(x) szigorúan monoton nő, tehát az f(x) függvénynek x=3 pontban lokális minimuma van.

Hasznos lehet, ha eredményeinket egy táblázatba is foglaljuk:

x	x<-1	x=-1	-1<x<3	x=3	x>3
Derivált fv. f’(x)	+	0 (zérus hely)	–	0 (zérus hely)	+
f(x)	Szig. mon. nő	Lokális maximum f(-1)=14/3	Szig. mon. csökken	Lokális minimum f(3)=-7	Szig. mon. nő

Ezen információk birtokában talán már számítógépes támogatás nélkül is el tudjuk készíteni a függvény grafikonját!

Az eredeti függvény zérus helyeinek a meghatározása nem ígérkezik könnyűnek. Egy harmadfokú polinomról van szó. A függvényvizsgálat után már lehet jobban megvizsgálni, hol is lehetnek zérus helyek. (Legtöbbször persze csak becsléssel.)

A függvény grafikonja megtekinthető az alábbi animáción:

 

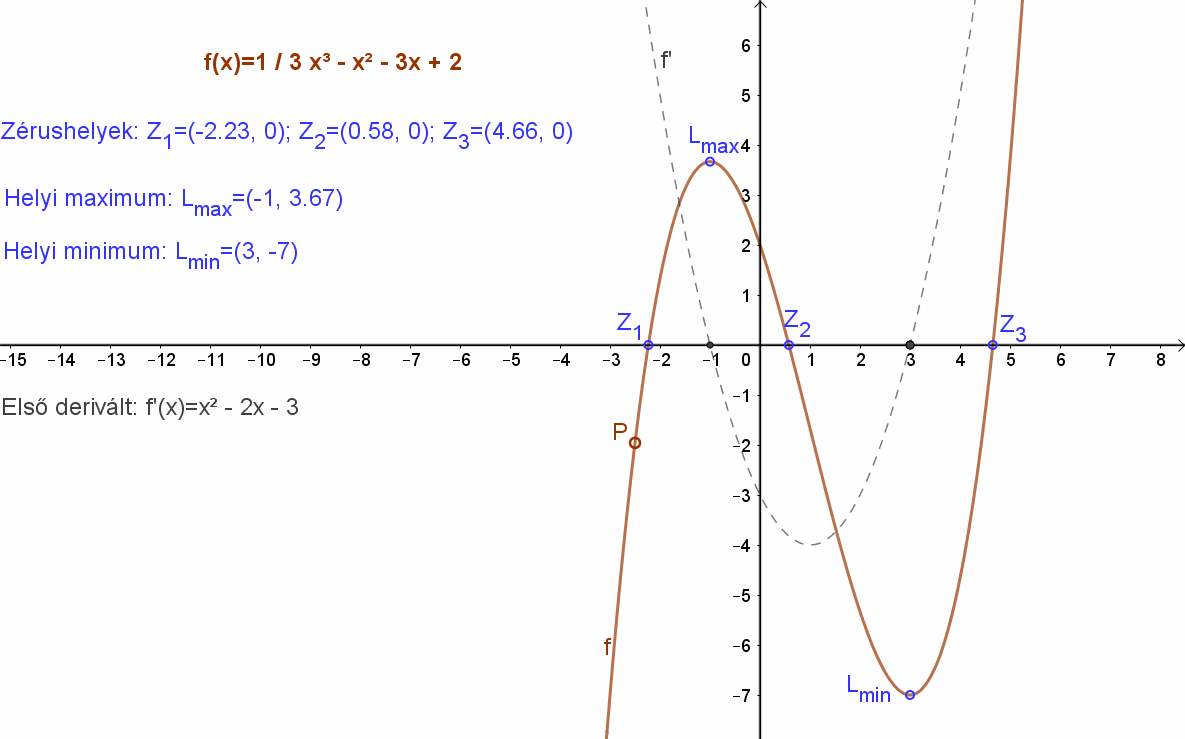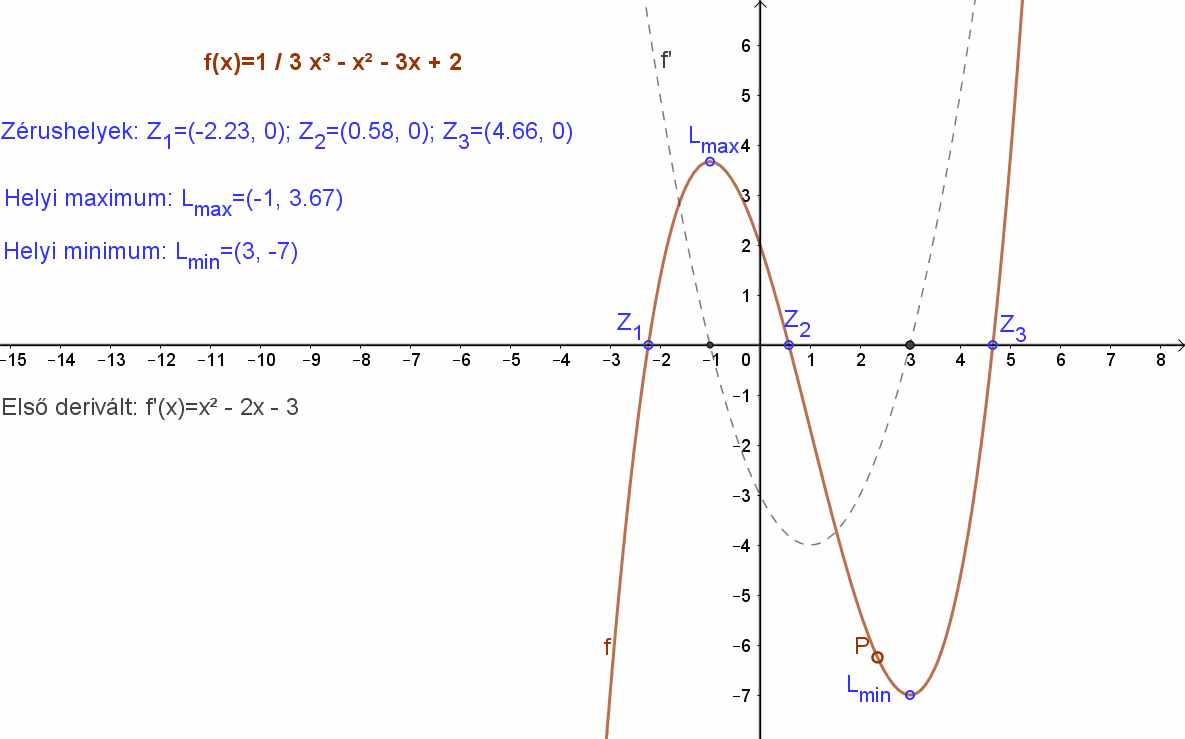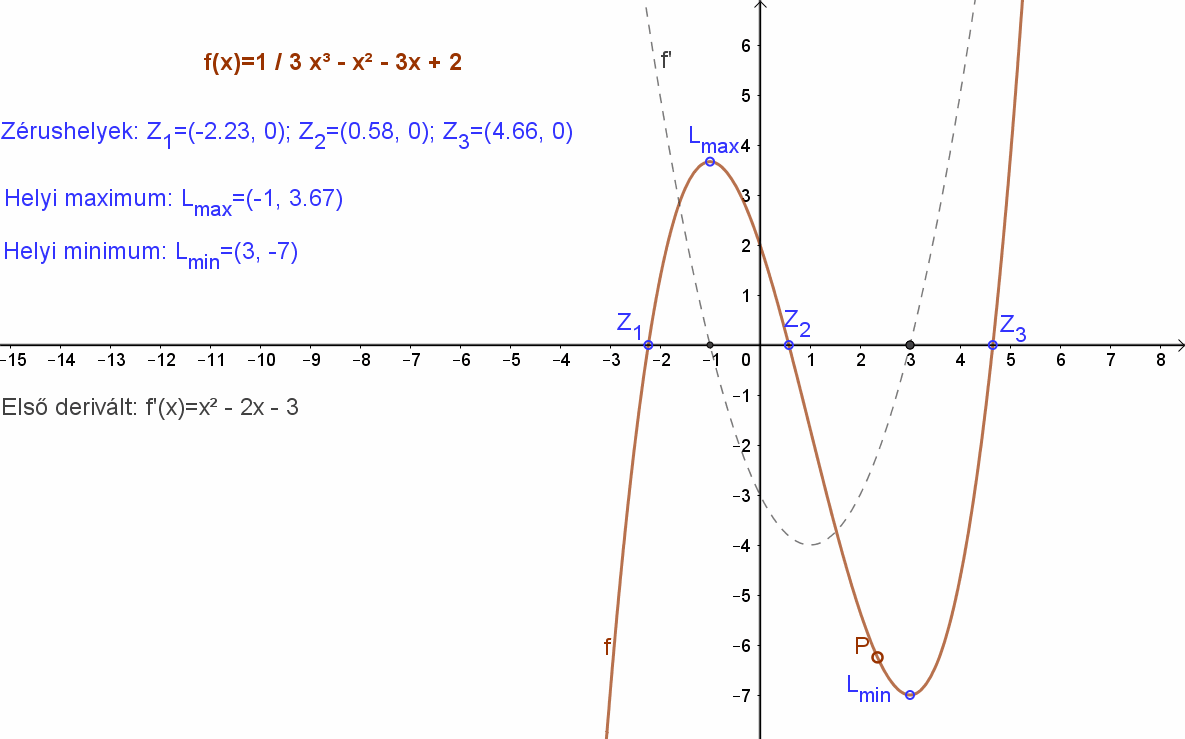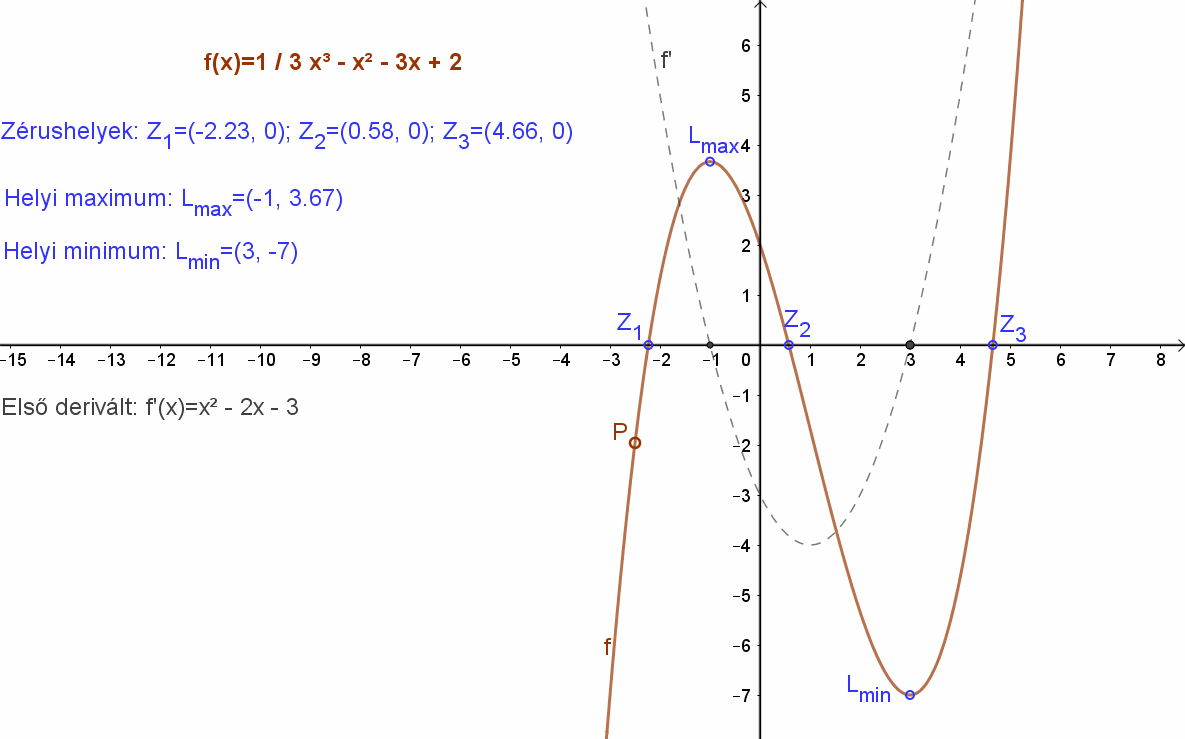
3. Függvény görbülete (Konvexitás, konkávitás)

A fenti animáción érdemes szemügyre venni, hogy az ​\( f(x)=\frac{1}{3}·x^3-x^2-3x+2 \)​ függvénynek van egy olyan intervallum, ahol konkáv és van ahol konvex. A lokális maximum egy konkáv, a lokális minimum egy konvex tartományban van.

Definíció szerint egy függvény konvex egy nyílt intervallumon, ha az intervallum bármely két pontját egy egyenessel összekötjük, akkor a függvény grafikonja a két pontot összekötő egyenes (szelő, húr) alatt halad. És ugyanígy: egy függvény konkáv egy nyílt intervallumon, ha az intervallum bármely két pontját egy egyenessel összekötjük, akkor a függvény grafikonja a két pontot összekötő egyenes (szelő, húr) felett halad. A deriválás segítségével a függvények konvexitását megvizsgálhatjuk a grafikon meglététől függetlenül.

Figyeljük meg a konvex és a konkáv függvények esetében a derivált függvény menetét.
„Úgy tűnik”, hogy ahol konkáv, ott a derivált függvény csökkenő, míg ahol az f(x) függvény konvex, ott a derivált függvény szigorúan monoton nő.

Tétel:

Legyen az f(x) függvény differenciálható az (a; b) nyílt intervallumban. Az f(x) függvény pontosan akkor (szigorúan) konvex ezen az (a; b) nyílt intervallumon, ha a derivált függvénye, az f’(x) függvény (szigorúan) monoton növekvő az (a; b) nyílt intervallumon.

Egy függvény menetét a derivált függvényének a segítségével lehet vizsgálni. Ebből az következik, hogy egy függvény konvexitásának vizsgálatához, a derivált függvény monotonitásának vizsgálatához a derivált függvény deriváltjára, azaz a második deriváltra is szükségünk lesz!

Tétel:

Legyen az f(x) függvény kétszer differenciálható az (a; b) nyílt intervallumban. Az f(x) függvény pontosan akkor (szigorúan) konvex ezen az (a; b) nyílt intervallumon, ha a második derivált függvénye, az f” (x) függvény pozitív (nemnegatív).

Nevezetes pont, ahol a függvény konvexitása megváltozik.

4. Függvény inflexiós pontja (pontjai)

Definíció:

Az x₀ pont az f(x) függvény inflexiós pontja, ha az x₀ pontban a függvény értelmezett és ott a függvény az konvexből konkávba vagy konkávból konvexbe megy át.

Az inflexiós pontban a függvényhez húzott érintő átmetszi a függvény görbéjét.

Tétel:

Ha az f(x) függvénynek x₀ pontban inflexiós pontja van és x₀ pont valamely környezetében kétszer differenciálható, akkor f ”(x)=0.

Ez az inflexiós pont létezésének szükséges, de nem elégséges feltétele.

Feladat:

Egészítsük ki az ​\( f(x)=\frac{1}{3}·x^3-x^2-3x+2 \)​ függvény jellemzését a függvény görbületének és inflexió pontjának a meghatározásával!

Megoldás:

Az ​\( f(x)=\frac{1}{3}·x^3-x^2-3x+2 \)​ függvény első deriváltja f(x)=x²-2x-3, így a függvény második deriváltja f”=2x-2.

Ennek zérushelye  I=(1,-5/3).

Az első derivált zérushelyei: Z^‘₁=(-1,0) , Z^‘₂=(3.0). A második derivált zérushelye: , Z^”₁=(1,0).
Ez a három pont négy intervallumot határoz meg a számegyenesen.

Ábrázoljuk mindhárom függvényt egymás alatt és kezdjük az elemzést a második deriválttal. Ennek zérushelye Z^”₁=(1,0). Itt az eredeti függvény értéke: f(1)=1/3 1^3-1^2-3∙1+2=-5/3. Így megkaptuk az inflexiós pont koordinátáit: I(1,-5/3).
A második derivált negatív, ha x<1, itt a függvény konkáv és pozitív, ha x>1. Itt a függvény konvex.
Hasznos lehet, ha eredményeinket egy táblázatba is foglaljuk:

x	x<-1	x=-1	-1<x<1	x=1	1<x<3	x=3	x>3
f ’	+	0	–	–	–	0	+
f ”	–			0	+
f(x)	Szig. mon. nő	Lokális maximum f(-1)=14/3	Szig. mon. csökken	f(1)=-5/3	Szig. mon. csökken	Lokális minimum f(3)=-7	Szig. mon. nő
	konkáv			Inflexiós pont	konvex

A függvény animációja kiegészítve a második deriválttal és az inflexiós ponttal: