A kúp, a henger és persze a hasábok felszíne síkba kiteríthető (a test hálója). Felszínüket az egyes testek hálóját alkotó síkidomok területeinek összege adja.
A gömbfelület a középiskolában eddig megismert felületektől alapvetően eltérő, ugyanis a gömbfelület síkba ki nem teríthető.
Felszínére vonatkozó összefüggés precíz levezetése túlmutat a normál középiskolai követelményeken. Az összefüggést azonban szemléletessé lehet tenni. Ennek érdekében elsőként be kell látnunk a következő segédtételt:
Adott csonkakúphoz mindig található olyan vele azonos magasságú egyenes körhenger, amelynek a palástja a csonkakúp palástjával egyenlő területű.
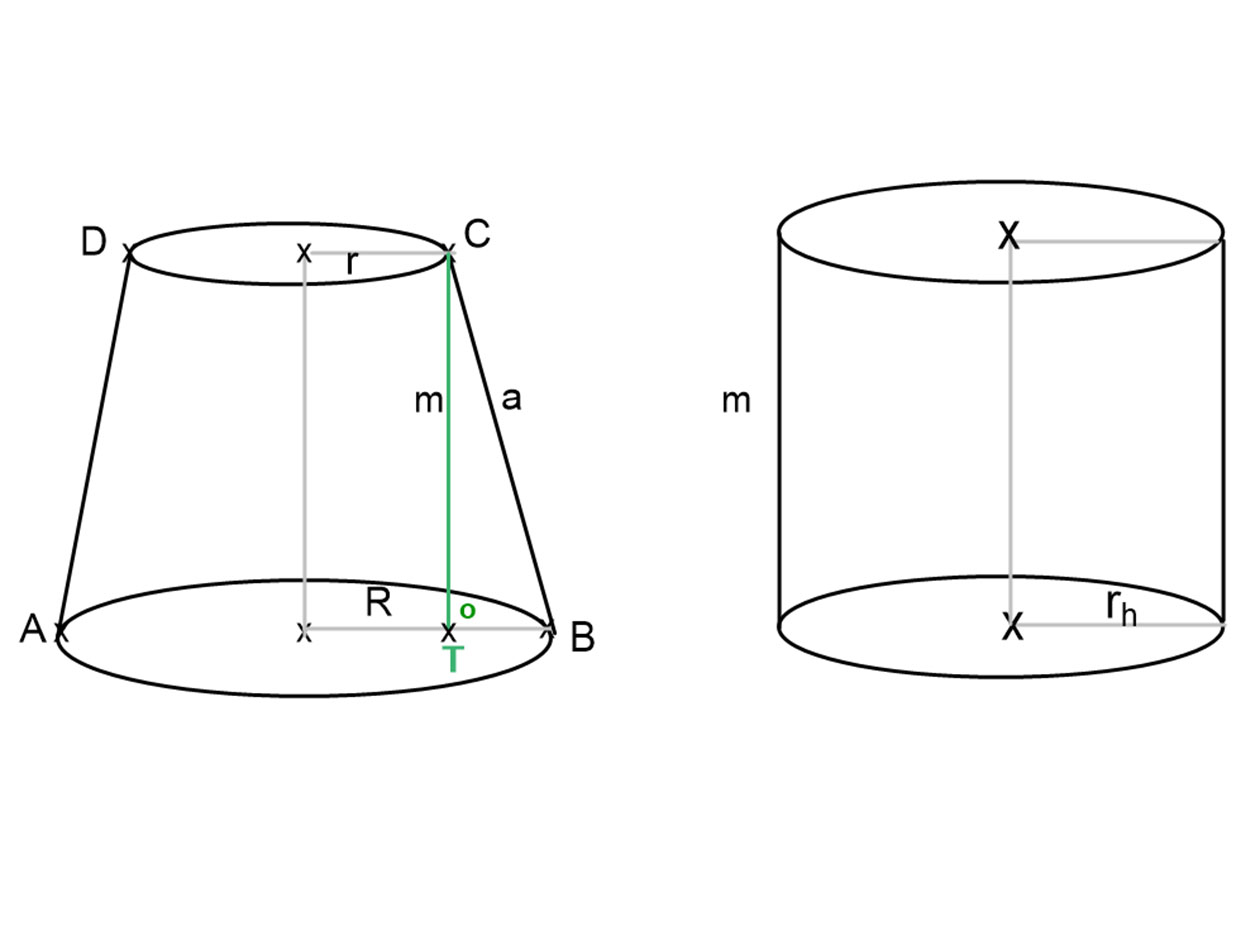Legyen adott egy csonkakúp, azaz adott alapkörének sugara (R), fedőkörének sugara (r) és a magassága (m). Ebből a három adatból a csonkakúp alkotója meghatározható. A mellékelt ábra jelölései szerint a BTC derékszögű háromszögre felírva Pitagorasz tételét: \( a=\sqrt{m^2+(R-r)^2} \).
Meg kell határoznunk annak a hengernek a sugarát (rh), amely a csonkakúppal azonos magasságú.
A csonkakúp palástjának felszíne: t1=(R+r)⋅π⋅a.
A henger palástjának felszíne: t2=2⋅rh⋅π⋅m.
A két terület a feltétel szerint egyenlő, tehát: 2⋅rh⋅π⋅m=(R+r)⋅π⋅a.
Az egyenletet π-vel egyszerűsítve és rh-ra kifejezve: \( r_{h}=\frac{(R+r)·a}{2·m} \).
Ez a kifejezés lehetővé teszi a henger sugarának a kiszámítását. De a kapott kifejezésnek szemléletes geometriai értelmet is tudunk adni. A jobb oldali kifejezésben az a változó a csonkakúp alkotója, m pedig a csonkakúp és a henger magassága.
A \( \frac{R+r}{2} \) kifejezés a csonkakúp alap és fedőkör sugarának a számtani közepe, amelynek geometriai jelentése: a csonkakúp síkmetszetének, a szimmetrikus trapéz középvonalának a fele.
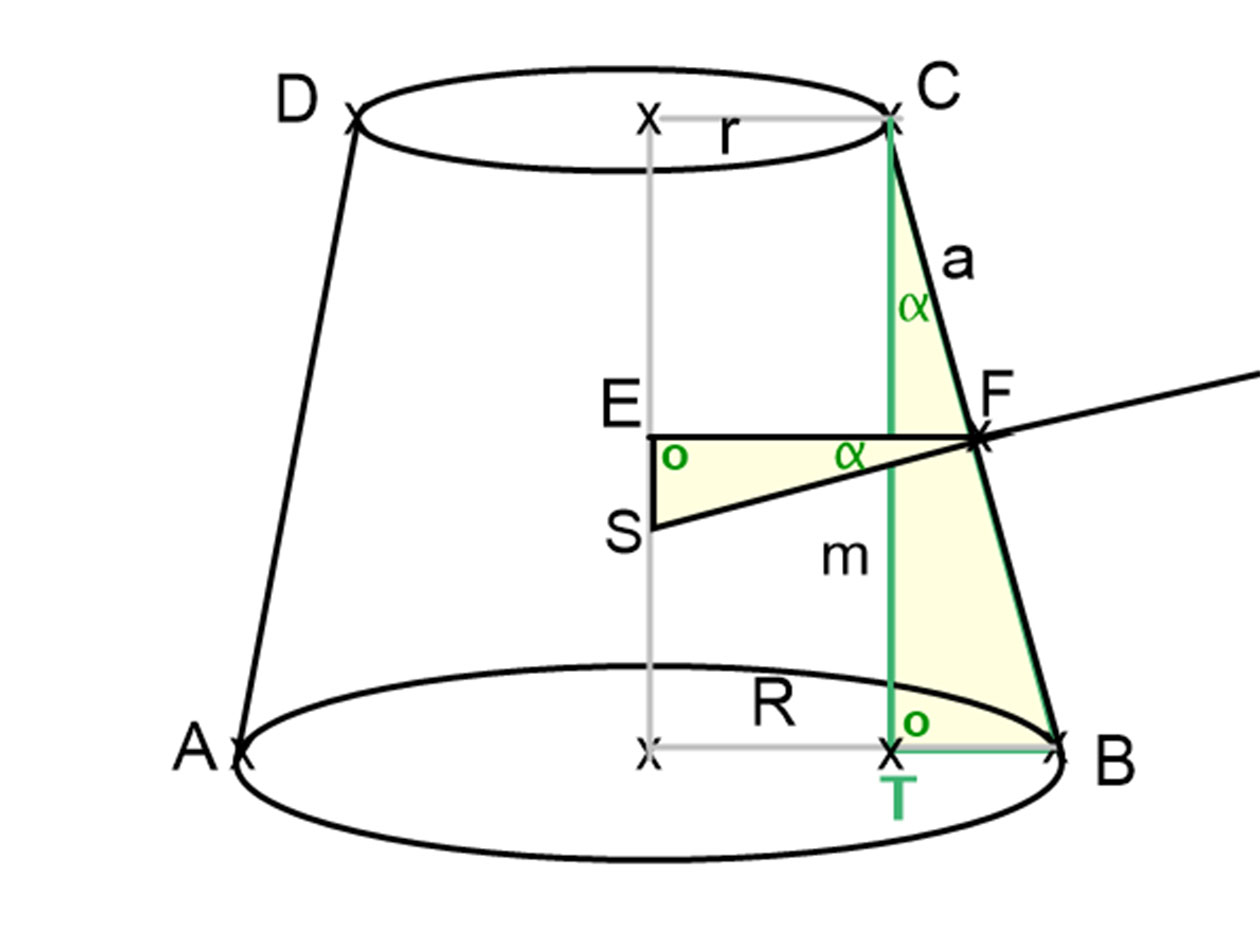A mellékelt ábrán az F pont a BC szár felezőpontja, az EF szakasz=\( \frac{R+r}{2} \) , hiszen az a trapéz középvonalának a fele. Ha ebben az F pontban a CB=a alkotóra, (a trapéz szárára) merőlegest állítunk, akkor létrejön egy FES derékszögű háromszög.
A kapott FES derékszögű háromszög hasonló a csonkakúp síkmetszetén látható CTB háromszöghöz, hiszen mindkettő derékszögű, és az EFS∠=TCB∠=α, mivel azonos típusú merőleges szárú szögek. A két háromszög hasonlóságából a megfelelő oldalak aránya következik, azaz: \( \frac{R+r}{2}:FS=m:a \).
Ezt szorzat alakba írva: \( FS·m=\frac{(R+r)·a}{2} \). Ebből az FS átfogót kifejezve: \( FS=\frac{(R+r)·a}{2·m} \ kifejezést kapjuk. Ez pontosan megegyezik a henger sugarára kapott képlettel, ami azt is jelenti egyben, hogy FS=rh.
Így az adott csonkakúphoz meg tudjuk szerkeszteni azt a vele azonos magasságú egyenes körhengert, amelynek palástja pontosan akkora területű, mint a csonkakúp palástja. Nem kell mást tenni, mint a csonkakúp egyik alkotójának felezőpontjában (F) olyan merőlegest kell állítani az alkotóra, amely metszi a csonkakúp tengelyét. A keletkezett (S) metszéspont és az alkotó (F) felezési pontja által meghatározott szakasz (FS) a keresett henger sugarát (rh) adja.
Ezután a segédtétel után rátérhetünk a gömb felszínének meghatározására.
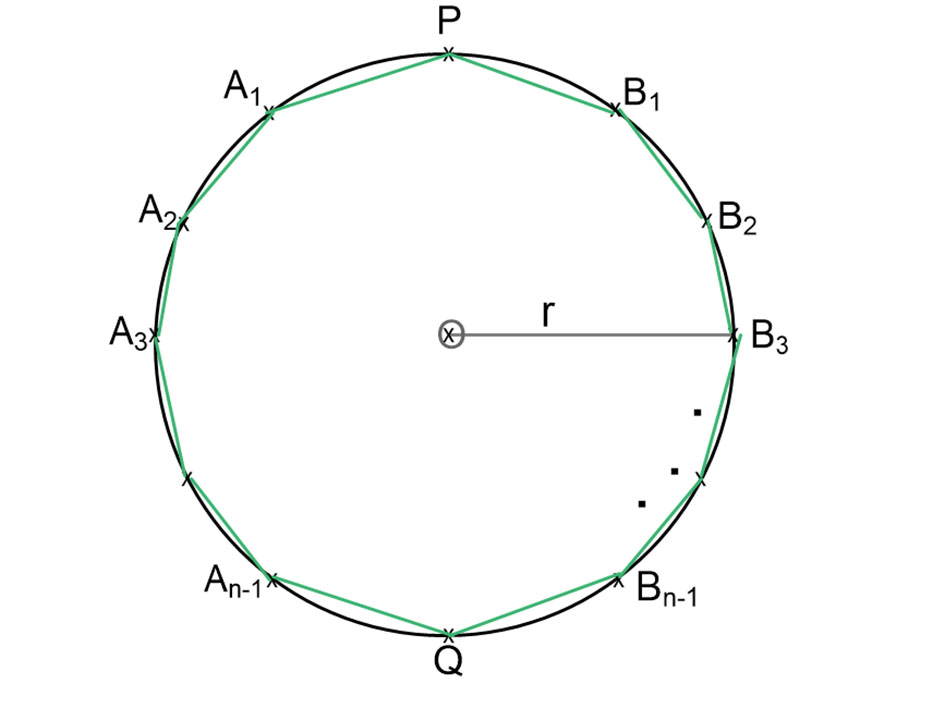Vegyünk fel egy O középpontú, r sugarú kört, és írjunk bele páros (2n) oldalszámú szabályos sokszöget. A mellékelt ábra jelölései szerint csúcsai:
P, A1, A22, A3, … An-1, Q, Bn-1,…B3, B2, B1.
Forgassuk meg ezt a kört a PQ átmérője körül!
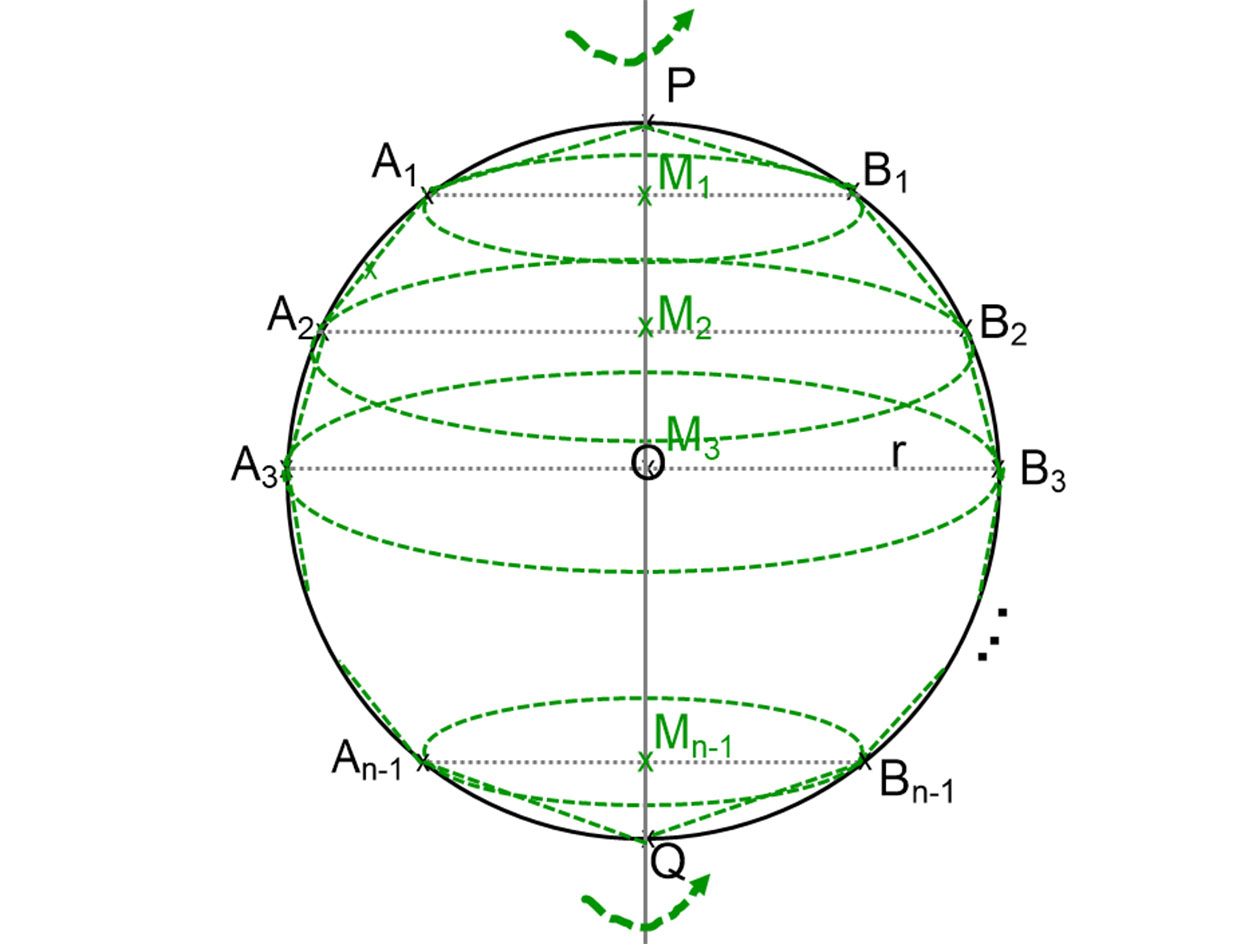A kör forgatásával kapunk egy O középpontú r sugarú gömböt.
A szabályos sokszög forgatásával kapott testet az A1B1, A2B2, A3B3, An-1Bn-1 egyenesekre illeszkedő, a gömb PQ tengelyére merőleges síkokkal rétegekre vágunk. Így n darab egyenes csonkakúphoz jutunk. Az alsó és felső kúpot most tekinthetjük olyan csonkakúpnak, amelynek fedőköre nulla sugarú.
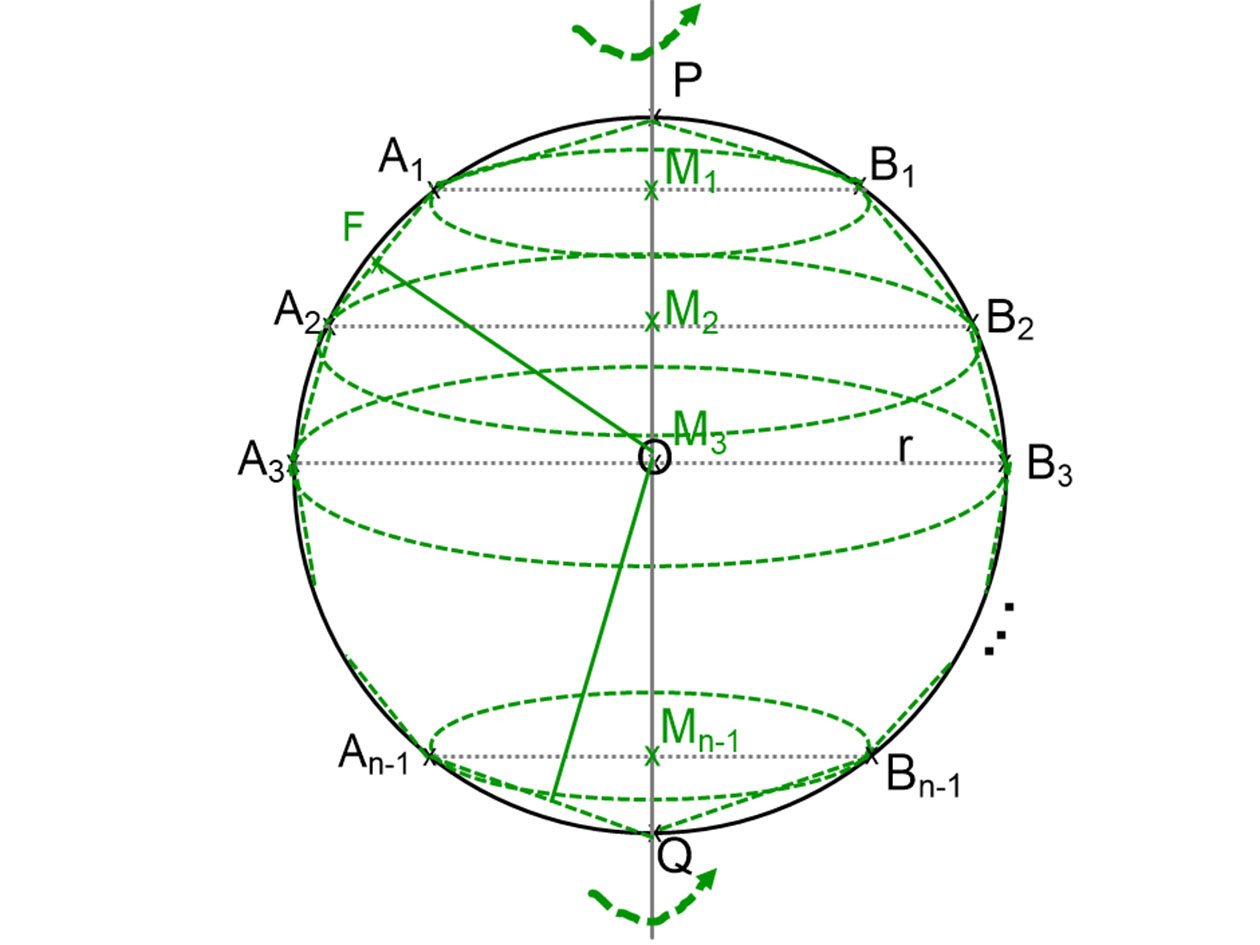A segédtétel szerint minden csonkakúphoz tudunk olyan egyenes körhengert szerkeszteni, amelynek a palástja a csonkakúp palástjával egyenlő területű. Mégpedig úgy, hogy a csonkakúp alkotójára, annak felezőpontjában olyan merőlegest állítunk, amely metszi a csonkakúp tengelyét. Nézzük most például azt a csonkakúpot, amelynek síkmetszete az A1A2B22B1 szimmetrikus trapéz. Ennek a csonkakúpnak a m magassága M2M1. Az A1A2 alkotó F felezőpontjában az A1A2-re állított merőleges át megy a kör, illetve a gömb O középpontján, hiszen A11A2 húrja ennek a körnek.
Mivel tudjuk, hogy a henger palástjának a területe: Phenger=2⋅rh⋅π⋅m, ahol m=M2M1, és rh=OF a segédtétel szerint, valamint Phenger egyenlő a csonkakúp palástjának területével.
Minden egyes csonkakúp palástjának területére hasonló formulát kaphatunk. Ezek összegzése megadja a szabályos sokszög forgatásával kapott test felszínét:
Pforgástest=2⋅OF⋅π⋅PM1+2⋅OF⋅π⋅M1M2+2⋅OF⋅π⋅M2M3+…+2⋅OF⋅π⋅Mn-2Mn-1+2⋅OF⋅π⋅Mn-1Q.
Az egyes tagokban szereplő közös 2⋅OF⋅π tényezőt kiemelve: Pforgástest=2⋅OF⋅π⋅(PM1+M1M2+M2M3+…+Mn-2Mn-1+Mn-1Q).
Itt azonban a zárójelben szereplő összeg éppen a kör, illetve a gömb 2r ármérőjével egyenlő.
Így tehát: Pforgástest=2⋅OF⋅π⋅2r, azaz Pforgástest=4r⋅OF⋅π.
Ha azonban a sokszög oldalainak n számát minél jobban növeljük, a kapott sokszög annál jobban odasimul a körvonalhoz, az OF távolság egyre kisebb mértékben tér el a kör illetve a gömb r sugarától. Az n oldalszámot minden határon túl növelve => OF=r következik, míg a forgástest felszíne a gömb felszínével lesz egyenlő. Ha tehát a Pforgástest=4r⋅OF⋅π kifejezésben az OF=r helyettesítést elvégezzük, kapjuk a gömb felszínére vonatkozó képletet:
Az r sugarú gömb felszíne: A=4⋅r2⋅π.
És ezt kellett bizonyítani.
Megjegyzés: „az oldalszám minden határon túl való növelése” az a gondolat, amely túlmutat a normál középiskolai anyagon. De ugyanevvel a gondolattal találkoztunk már a henger, és a kúp térfogatánál is.
Feladat:
Egy gömbbe írt kocka felszíne 144 cm2. Mekkora a gömb felszíne?
(Összefoglaló feladatgyűjtemény 2411. feladat.)
Megoldás:
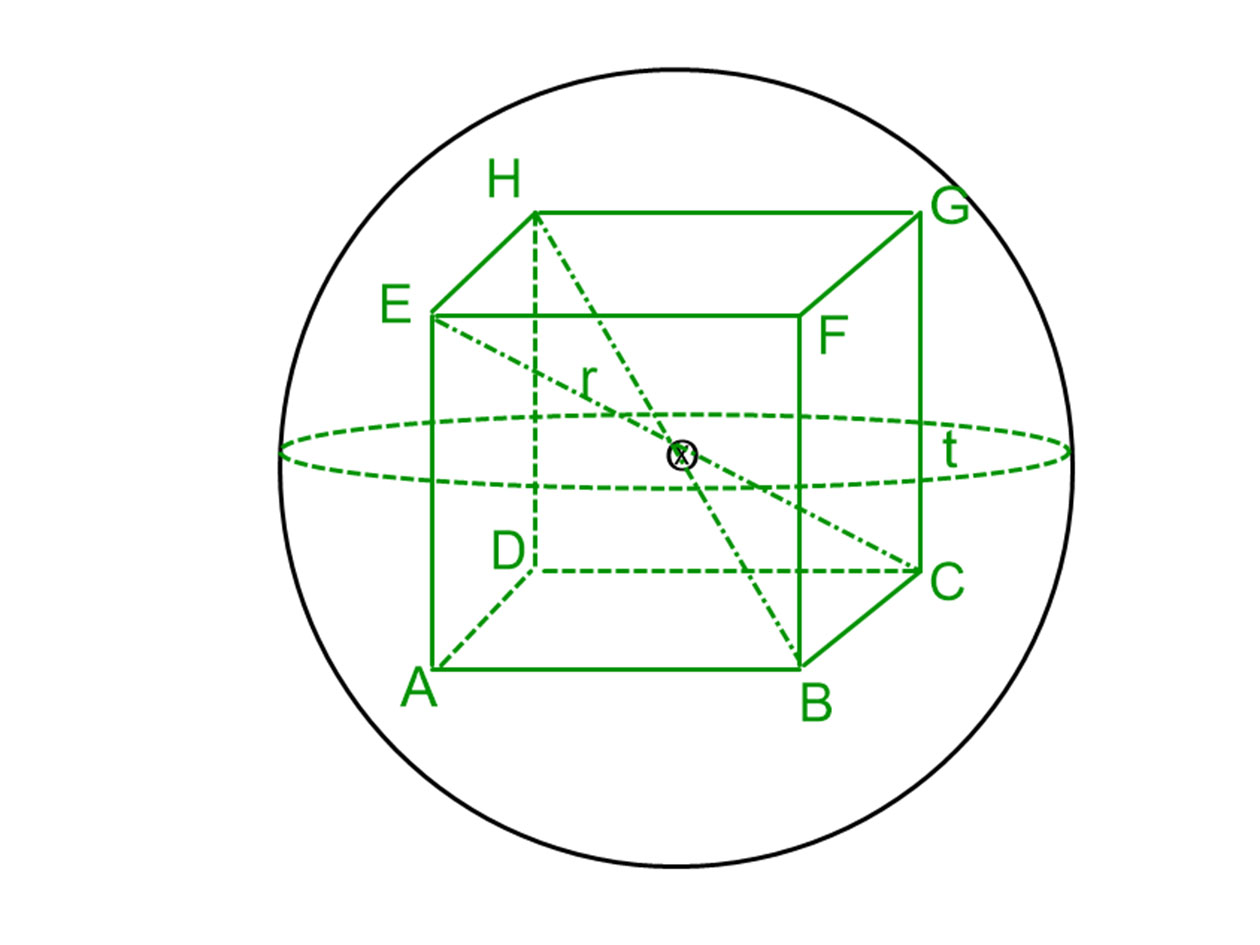Tudjuk, hogy a kocka felszíne: Akocka=6⋅a2, ahol az a változó a kocka élét jelenti. A megadott adattal tehát: 144=6⋅a2. Ebből a2=24 és a=\( a=\sqrt{24}=2\sqrt{6} \) .
A kocka testátlója: \( t=a\sqrt{3} \), ezért a feladatban szereplő kocka EC testátlója: \( t=2\sqrt{6}·\sqrt{3}=6\sqrt{2} \).
A gömb sugara a testátló fele: \( r_{gömb}=3\sqrt{2} \).
Így a gömb felszíne: \( A_{gömb}=4·(3\sqrt{2})^2· π =72 π \)cm2 vagyis A≈226,2 cm2.
Comments are closed, but trackbacks and pingbacks are open.