A hiperbola egyenletének meghatározásához induljunk ki a hiperbola definíciójából!
Definíció:
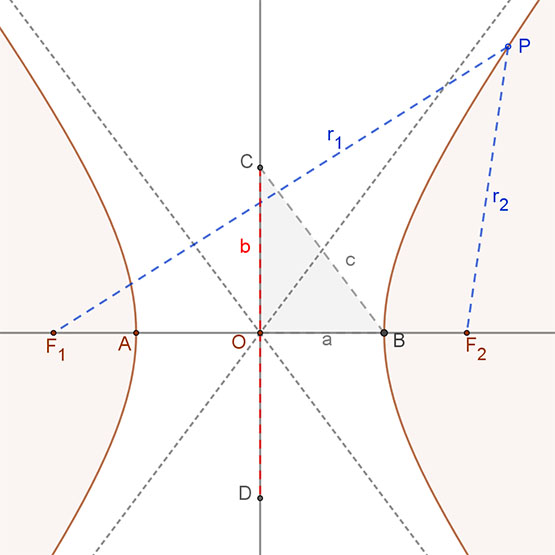
A hiperbola azoknak a P pontoknak az összessége (mértani helye) a síkban, amelyek a sík két adott pontjától, az F1 és F2 fókuszpontoktól való távolságaik (r1, és r2 vezérsugarak) különbségének abszolút értéke állandó (2a).
Ez a távolság kisebb kell legyen, mint a két fókuszpont távolsága (2c).
 Formulával: hiperbola={P|(|d(P,F1)-d(P,F2)|)=|r1-r2|=állandó=2a<d(F<1;F2).
Formulával: hiperbola={P|(|d(P,F1)-d(P,F2)|)=|r1-r2|=állandó=2a<d(F<1;F2).
A 2a távolság a hiperbola valós tengelye (a mellékelt ábrán az AB távolság, míg erre merőleges a hiperbola 2b hosszúságú képzetes tengelye (CD távolság).
A mellékelt ábrán az OBC derékszögű háromszögben felírva a Pitagorasz tételt: c2=a2+b2.
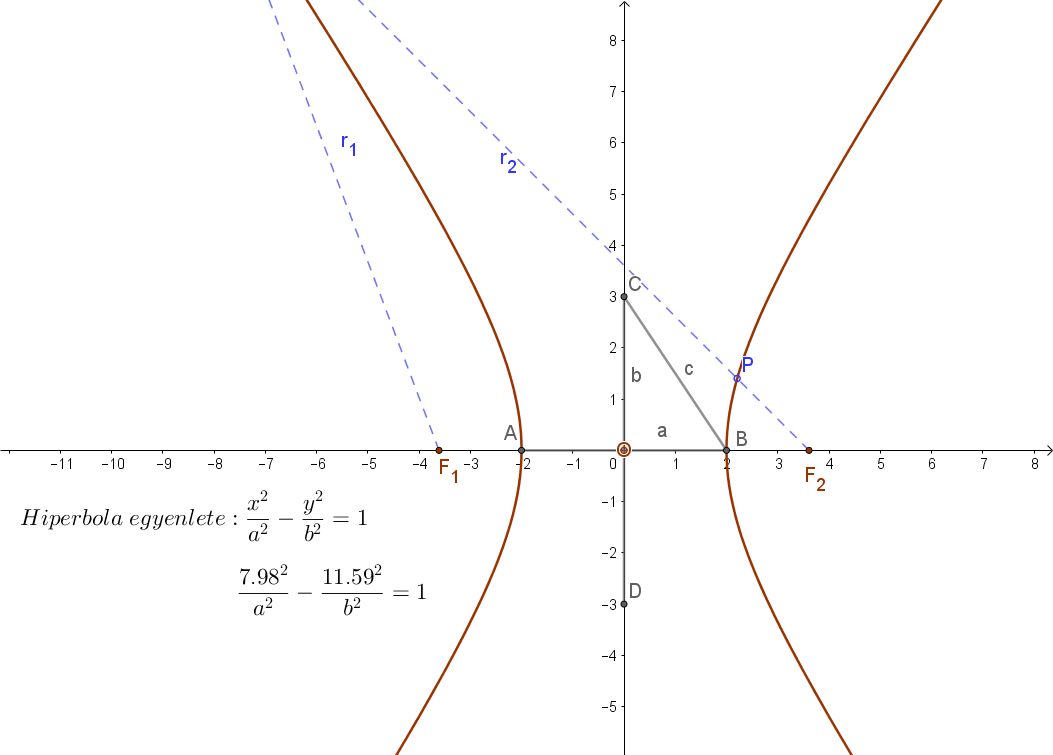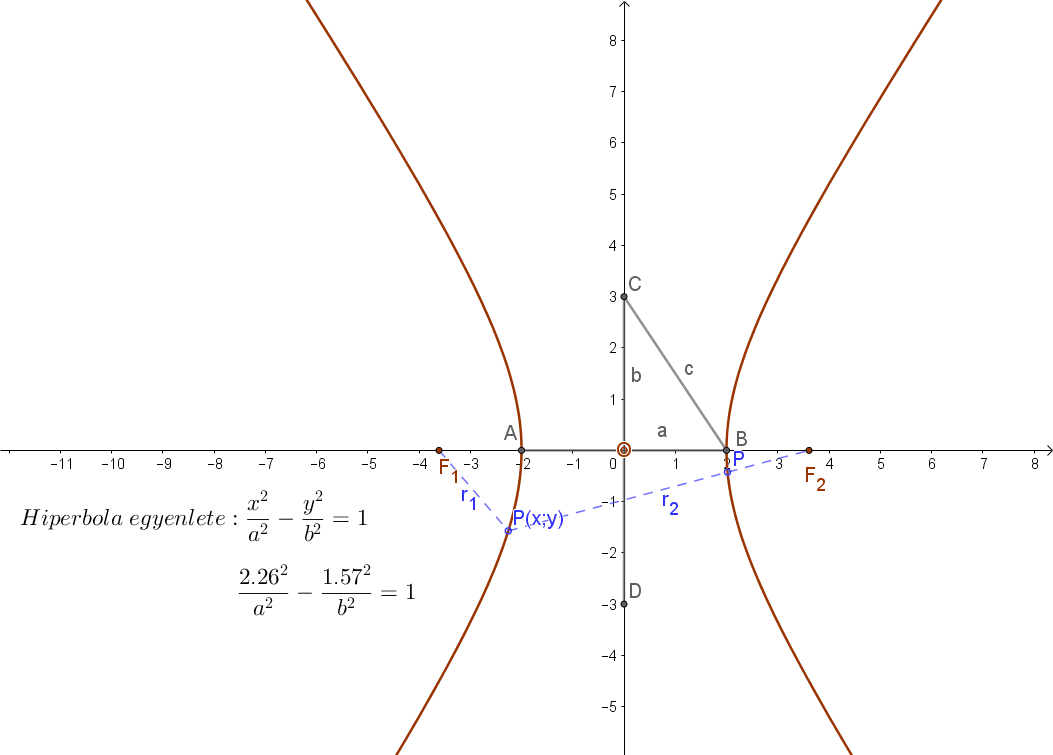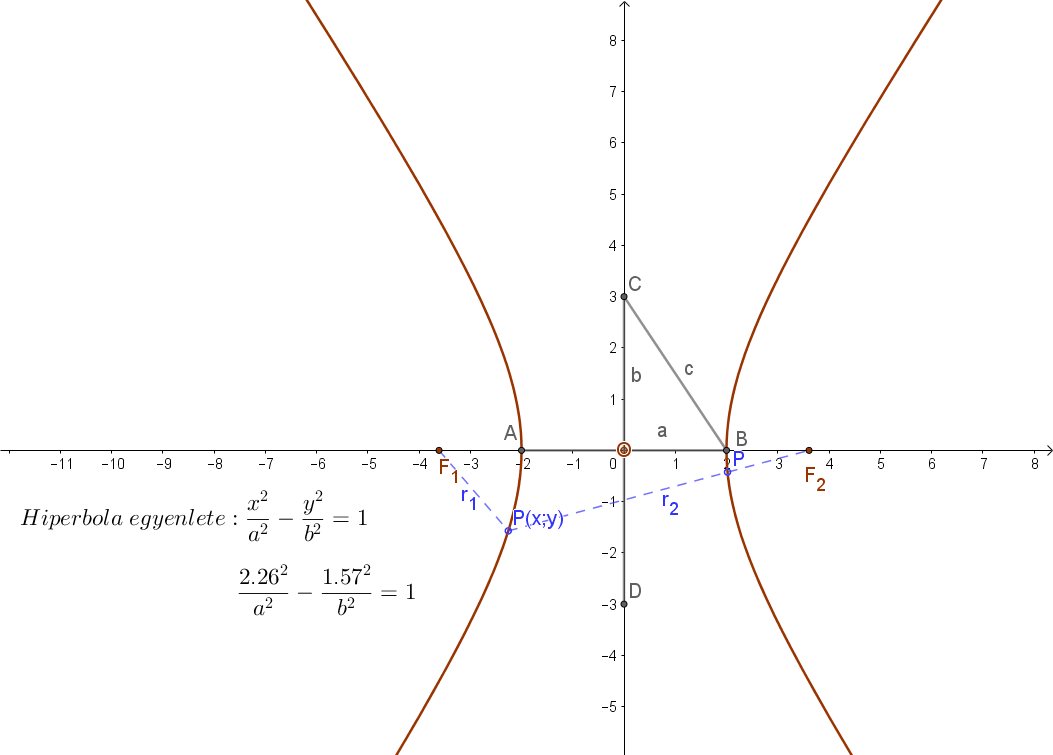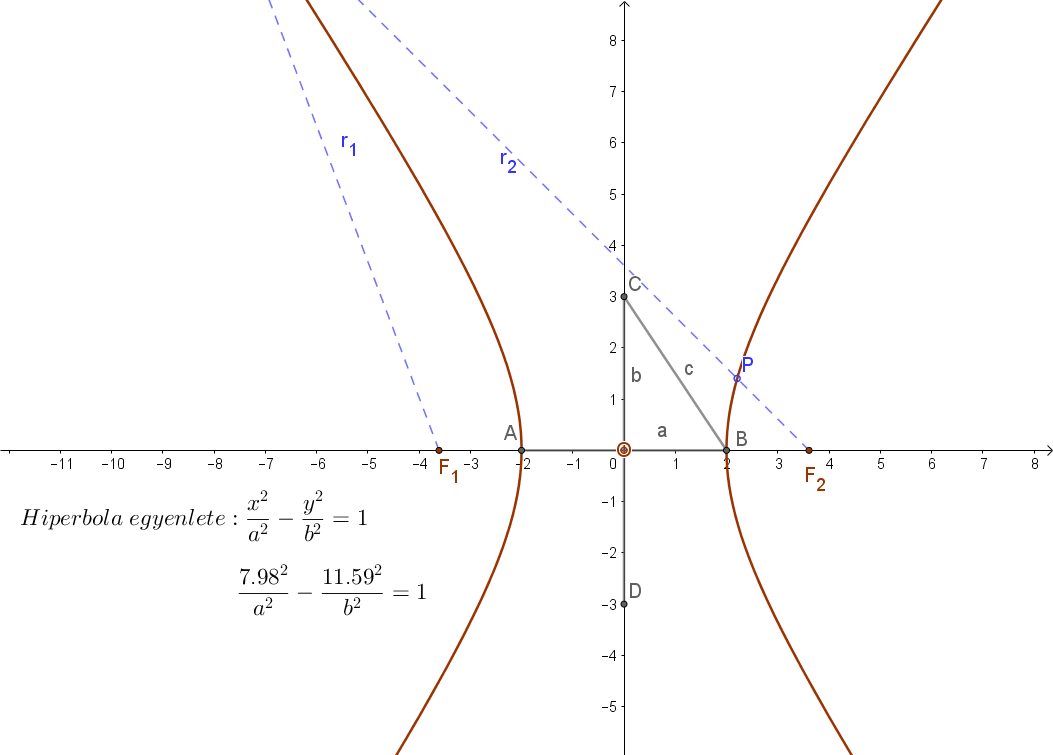
Helyezzük el a hiperbolát a koordináta rendszerben úgy hogy a 2a hosszúságú valós tengelye az „x”, a 2b hosszúságú képzetes tengelye pedig az „y” tengelyre essen. Ekkor a hiperbola középpontja az origó, fókuszpontjainak koordinátái pedig: F1(-c;0) és F2(c;0).
A hiperbola egyenletéhez fel kell írni a hiperbola tetszőleges P(x;y) pontjának a távolságát a két fókuszponttól. A hiperbola definíciója szerint ennek a két távolságának különbség állandó (2a) kell legyen. Ebből kapjuk majd meg a hiperbola egyenletét.
Állítás:
A fent módon elhelyezett hiperbola P(x;y) pontjaira nézve érvényes középponti egyenlete: \( \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \).
Bizonyítás:
1. P(x;y) pont távolsága az F1(-c;0) fókuszponttól: d(P;F1):![]()
Itt felhasználtuk a két pont távolságára tanult összefüggést.
2. P(x;y) pont távolsága az F2(c;0) fókuszponttól: d(P;F2):
![]()
A két távolság különbsége (abszolút értékben) adja a hiperbola egyenletét.: |d(P;F1)-d(P;F2)|=2a.
Azaz: ![]()
Próbáljuk azonban ezt átalakítani. Az átalakítás során az ellipszis egyenleténél alkalmazott lépéseket fogjuk itt is használni. Az abszolút érték miatt azonban két esetet fogunk nézni:
1. d(P;F1)>d(P;F2). Ez a hiperbola jobb oldali ága. (r1>r2).
2. d(P;F1)<d(P;F2). Ez a hiperbola bal oldali ága. (r1<r2).
1. Nézzük előbb a hiperbola jobb oldali ágát. (r1>r2).
Ebben az esetben a hiperbola egyenlete így írható:![]()
Átrendezve:![]()
Négyzetre emelve: ![]()
Mindkét oldalról y2 elvéve: ![]()
Zárójeleket felbontva: ![]()
A mindkét oldalon egyező tagokkal egyszerűsítve és átrendezve:![]()
4-gyel egyszerűsítve: ![]()
Átrendezve: ![]()
Négyzetre emelve: ![]()
Beszorozva:![]()
Egyező tagokkal egyszerűsítve:![]()
Átrendezve: ![]()
A baloldalon x2-t kiemelve:![]()
Felhasználva a c2=a2+b2 összefüggést: ![]()
Átrendezve:![]()
![]() A jobb oldalon a2-t kiemelve:
A jobb oldalon a2-t kiemelve:
![]() Újra felhasználva a c2=a2+b2 összefüggést:
Újra felhasználva a c2=a2+b2 összefüggést:
A jobb oldalon szereplő taggal átosztva (a és b távolságok, nem lehetnek nullák)
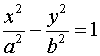
2. d(P;F1)<d(P;F2). Ez a hiperbola bal oldali ága. (r1<r2).
Ebben az esetben a hiperbola egyenlete így írható:![]()
Ebben az esetben is a fentiekhez hasonló lépéseken át juthatunk el a hiperbola egyenletének már megismert alakjához:
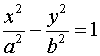


Comments are closed, but trackbacks and pingbacks are open.