Vektor abszolút értéke

Definíció:

Vektor abszolút értékén a vektor hosszát értjük.

A bázisvektorok által meghatározott koordináta-rendszerben minden koordinátáival adott vektort tekinthetünk helyvektornak.

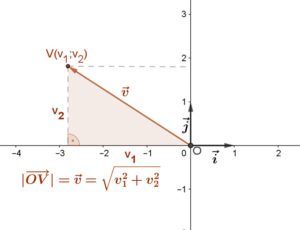A vektor koordinátáinak megrajzolásával egy derékszögű háromszöget kapunk (ha a vektor nincs a koordináta-tengelyek valamelyikén). Ennek átfogója a vektor abszolút értéke, mint szakasz. Befogói, mint távolságok a koordináták abszolút értékei. Pitagorasz tételével kapjuk az alábbi összefüggést: ​\( |\overrightarrow{OV}=|\vec{v}|=\sqrt{v_{1}^2+v_{2}^2} \)​

Tétel:

Egy vektor abszolút értéke egyenlő koordinátáinak négyzetösszegéből vont négyzetgyökével.

Ez az összefüggés akkor is helyes eredményt ad, ha a vektor illeszkedik valamelyik tengelyre, azaz ha valamelyik koordinátája nulla.