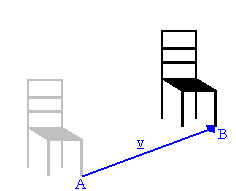
„Told el a széket!” „Merre?” „Mennyire?”
Az eltolás végrehajtásához szükségünk van: az eltolás mértékének és irányának a megadására.
Az eltolást mint geometriai transzformációt irányított szakasszal, vektorral adjuk meg.
Definíció:
Az irányított szakaszt vektornak nevezzük.
Jelölések: \( \vec{v}=\underline{v}=\overrightarrow{AB} \)
Vektor hossza:
A vektor hosszát a vektor abszolút értékének nevezzük, és a következőképpen jelöljük: \( \left|\underline{v}\right| =\left|\overrightarrow{AB} \right| \) .
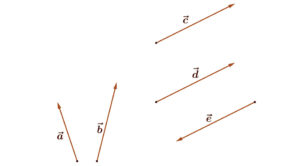Ha két vektorhoz van olyan egyenes, amelyik mindkettővel párhuzamos, akkor a két vektort párhuzamos, vagyis egyállású vektoroknak nevezzük. A mellékelt ábrán egyállású vektorok az \( \vec{c}||\vec{d}||\vec{e} \)
Definíció:
Két vektor egyenlő, ha abszolút értékük egyenlő (egyenlő hosszúak), párhuzamosak (egyállásúak), és azonos irányúak.
A fenti ábrán a \( \vec{c} \) és a \( \vec{d} \)vektorok egyenlők: \( \vec{c} \) = \( \vec{d} \).
Definíció:
Ha két vektor egyállású, abszolút értékük egyenlő és ellentétes irányúak, akkor a két vektor egymás ellentettjének mondjuk.
A fenti ábrán az \( \vec{e} \) vektor a \( \vec{c} \) és a \( \vec{d} \) vektorok ellentett vektora.
Ezt így jelöljük: \( \vec{e}=-\vec{c} \) és \( \vec{e}=-\vec{d} \).
Definíció:
Ha egy vektor abszolút értéke nulla, akkor azt nullvektornak mondjuk. A nullvektor állása és iránya tetszőleges.
Egy vektort tehát abszolút értéke, állása és iránya jellemez.
Comments are closed, but trackbacks and pingbacks are open.