Kör sugara, húrja és kerületi szög összefüggése

Állítás:

Egy kör r hosszúságú sugara, az a hosszúságú húrja és az ahhoz tartozó α kerületi szög között a következő összefüggés áll fenn: a=2⋅r⋅sinα.

A bizonyítást három esetre érdemes elvégezni.

1. Amikor a húrhoz tartozó kerületi szög hegyesszög.
2. Amikor a húrhoz tartozó kerületi szög derékszög.
3. Amikor a húrhoz tartozó kerületi szög tompaszög.

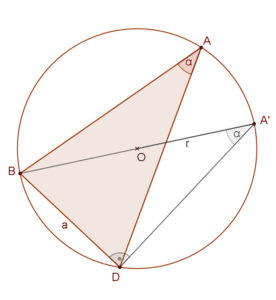1. eset. A mellékelt ábra azt az esetet mutatja, amikor a BC=a húrhoz tartozó BAC∠=α hegyesszög.

Húzzuk meg a B pontból induló átmérőt. Ennek végpontja legyen A’. Így BA’=2r.
Az A’CB háromszög derékszögű, A’CB∠=90°. Ugyanakkor az A’ csúcsnál lévő BA’C∠=BAC∠=α, hiszen mindketten a BC ívhez tartozókerületi szögek.

Az A’CB’ derékszögű háromszögben felírva a BAC=α szögre felírva a szög szinuszát:

sinα=BC/BA’, azaz sinα=a/2r.

Ez éppen az állítást jelenti: a=2⋅r⋅sinα.

2. eset. A BC=a húrhoz tartozó BAC∠=α=90° derékszög.

Az BAC háromszög derékszögű háromszögben a BC=a húr a kör átmérője, azaz a=2r. Mivel sin90°=1, ezért a=2rsinα most is igaz.

Ez éppen az állítást jelenti: a=2⋅r⋅sinα.

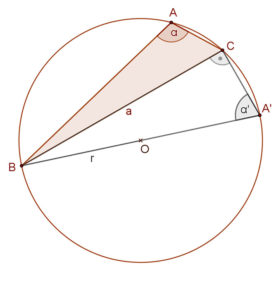3. eset. A mellékelt ábra azt az esetet mutatja, amikor a BC=a húrhoz tartozó BAC∠=α tompaszög.

Húzzuk meg a B pontból induló átmérőt. Ennek végpontja legyen A’. Így BA’=2r.
Az A’CB háromszög derékszögű, A’CB∠=90°. Ugyanakkor az A’ csúcsnál lévő BA’C∠=α’ Mivel a BA’CA négyszög húrnégyszög, ezért α’=180°-α.
Az A’CB’ derékszögű háromszögben felírva a BAC=a szögre felírva a szög szinuszát:
Sinα’=BC/BA’, azaz  sin(180°-α)= a/2r.
Mivel sin(180°-α)=sinα, ezért sinα=a/2r.

Ez éppen az állítást jelenti: a=2⋅r⋅sinα.

Ez a tétel lehetőséget teremt a háromszög köré írt köre sugarának meghatározására, ha ismerjük egy oldalát és a vele szemközti szögét.

Ugyancsak ez a tétel teremt kapcsolatot a háromszög területe és a köré írt kör sugara között.
Ha adott a háromszög két oldala és közbezárt szöge (például b, c és a ), akkor a háromszög területe a következőképpen számítható ki: t=(b⋅c⋅sinα)/2.

Ha itt a sinα helyére az ebben a tételben megfogalmazott állítást helyettesítjük, nevezetesen: sinα =a/2r, akkor a következő összefüggést kapjuk: t=abc/4r .