A háromszög területének kiszámítása gyakori feladat. Különböző képletek segítenek ebben.
1. A legismertebb képlet az oldal és a hozzátartozó magasság ismeretében határozza meg a területet: TΔ=a⋅ma/2.
2. Háromszög területe három oldal ismeretében. Ez a Héron képlet: \( t=\sqrt{s(s-a)(s-b)(s-c)} \) , ahol s a háromszög kerületének a fele, azaz \( s=\frac{a+b+c}{2} \).
3. Háromszög területe és a beírt kör sugara (rb) közötti összefüggés: TΔ=rb⋅s, ahol s a háromszög kerületének a fele, azaz \( s=\frac{a+b+c}{2} \).
4.Háromszög területe, oldalai és a köréírt kör sugara (rk) közötti összefüggés: TΔ=a⋅b⋅c/(4⋅rk).
5. A háromszög területe a két oldalból és a közbezárt szög segítségével: TΔ=a⋅c⋅sin(β)/2.
Ez utóbbi levezetése látható itt.
Legyen adott a háromszög két oldala, például a és c, valamint az általuk közbezárt β szög. Itt két esetet vizsgáljunk:
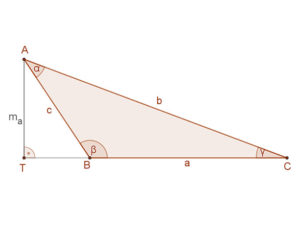
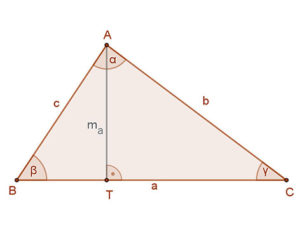
A levezetés lépesei:
1. A háromszög területét a \( t=\frac{a·m_{a}}{2} \) képlet szerint számítjuk.
2. Most itt adott az a oldal, de nem ismert az ma magasság. Adott viszont a c oldal.
3. Az ABT derékszögű háromszögben \( sinβ=\frac{m_{a}}{c} \) . Átrendezve: ma=c⋅sinβ.
4. Ezt behelyettesítve a területképletbe: \( t=\frac{a·c·sinβ}{2} \).
5. Mivel sinβ=sin(180°-β), ezért ez az összefüggés független attól, hogy a β szög hegyes, vagy tompaszögű.
6. Tehát a háromszög területét megkapjuk, ha a két oldalának szorzatát megszorozzuk a közbezárt szög sinusával, és a kapott eredményt osztjuk kettővel: TΔ=a⋅c⋅sin(β)/2.
A kapott összefüggés abban az esetben is alkalmazható, amikor a közbezárt szög derékszög, hiszen sin90° =1.
Ennek az összefüggésnek a segítségével bizonyítjuk be a szinusz tételt.


Comments are closed, but trackbacks and pingbacks are open.