Hérón görög matematikusról elnevezett képlet segítségével a háromszög területe könnyen kiszámítható a három oldal ismeretében.
A Héron képlet:
\( t=\sqrt{s(s-a)(s-b(s-c)} \) ahol s a háromszög kerületének a fele, azaz \( s=\frac{a+b+c}{2} \).
Ezt az összefüggést valószínűleg Arkhimédész fedezte fel, de Hérón bizonyította be elsőként.
A képlet levezetése:
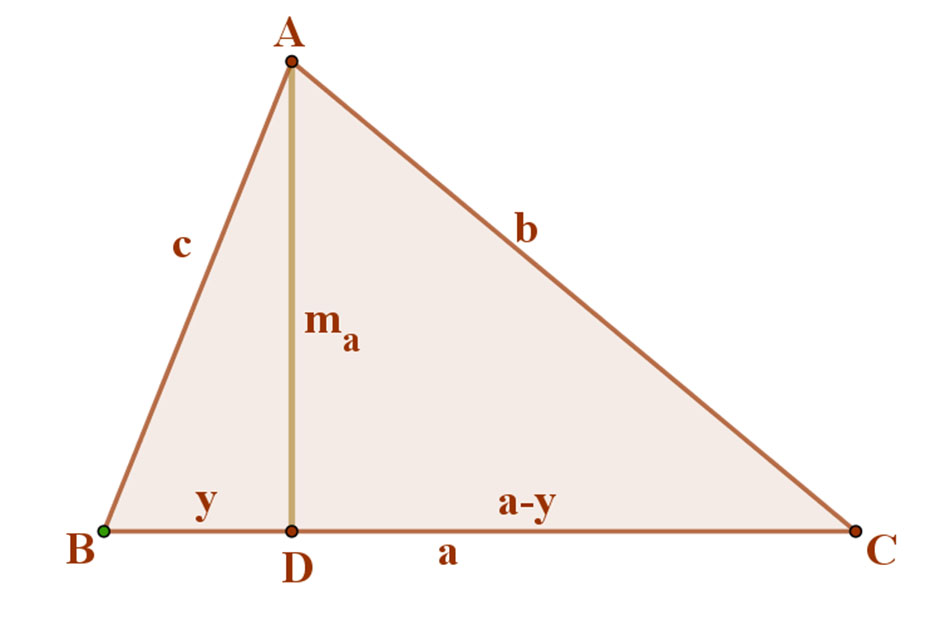
Induljunk ki a háromszög területének közismert képletéből: \( t=\frac{a·m_{a}}{2} \)
Mivel a magasságot nem ismerjük, fejezzük ki ma-t a megadott három oldal segítségével!
Az ma magasság a szemben lévő oldalt két szakaszra bontja. Jelöljük a BD szakaszt y-nal. BD=y, így DC=a-y.
Ennek érdekében írjunk fel két összefüggést Pitagorasz tétele segítségével: az ABD és DCA háromszögekben:
\( c^{2}=y^2+{m_{a}}^2 \)
\( b^{2}=(a-y)^2+{m_{a}}^2 \)
Az egyenletrendszerből fejezzük ki y-t:
\( b^{2}=(a-y)^2+c^2-y^2 \)
\( b^2=a^2-2ay+y^2+c^2-y^2 \)
\( 2ay=a^2+c^2-b^2 \)
\( y=\frac{a^2+c^2-b^2}{2a} \)
Ezt helyettesítsük vissza az ABD háromszögben felírt Pitagorasz tételbe:
\( c^2=\left( \frac{a^2+c^2-b^2}{2a} \right) ^2+{m_{a}}^2 \)
Fejezzük ki ebből ma-t!
\( {m_{a}}^2=c^2-\left( \frac{a^2+c^2-b^2}{2a} \right) ^2 \), azaz
\( {m_{a}}^2=\frac{4a^2c^2-\left( a^2+c^2-b^2 \right) }{4a^2}^2 \)
\( m_{a}=\sqrt{\frac{4a^2c^2-\left( a^2+c^2-b^2 \right) }{4a^2}^2} \)
Ezt helyettesítsük be a háromszög területének jól ismert képletébe:
\( t=\frac{a·m_{a}}{2} \),azaz \( t=\frac{a}{2}\sqrt{\frac{4a^2c^2-\left( a^2+c^2-b^2 \right) }{4a^2}^2} \)
Vigyük be \( \frac{a}{2} \)-t a négyzetgyök alá és ott egyszerűsítsünk a2 -tel:
\( t=\sqrt{\frac{4a^2c^2-\left( a^2+c^2-b^2 \right) }{16}^2} \)
A kapott összefüggés már ebben az alakjában is alkalmas arra, hogy a három oldalból kiszámítsuk a háromszög területét. Azonban egy kis átalakítással az állításban szereplő egyszerűbb alakhoz juthatunk a következő módon:
Vegyük észre, hogy a négyzetgyök alatt a számlálóban két négyzet különbsége szerepel, így a jól ismert x2-y2=(x-y)(x+y) azonosságot felhasználva a számláló szorzattá alakítható.
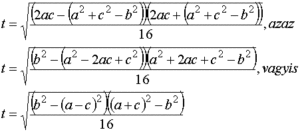
A számlálóban szereplő két tényezős szorzatot a fent említett azonossággal tovább tudjuk bontani immár négy tényezős szorzattá:
Mivel \( s=\frac{a+b+c}{2} \), így \( \frac{b+c-a}{2}=\frac{a+b+c-2a}{2}=s-a \) és \( \frac{a+c-b}{2}=\frac{a+b+c-2b}{2}=s-b \) és \( \frac{a+b-c}{2}=\frac{a+b+c-2c}{2}=s-c \)
Így ezt felhasználva a bizonyítandó állítást kapjuk, vagyis:
\( t=\sqrt{s(s-a)(s-b)(s-c)} \)
Comments are closed, but trackbacks and pingbacks are open.