Tétel:
Bármely háromszögben az oldalak aránya megegyezik a velük szemközti szögek szinuszának arányával.
A háromszögek területe meghatározható bármelyik két oldalának és a közbezárt szögének ismeretében, függetlenül attól, hogy az hegyes vagy tompa esetleg derékszög: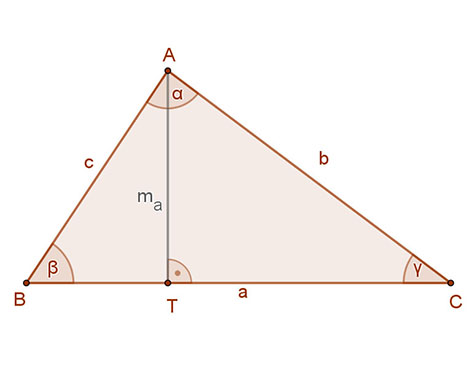
\( t=\frac{a·c·sinβ}{2} \), vagy \( t=\frac{a·b·sinγ}{2} \) vagy \( t=\frac{b·c·sinα}{2} \).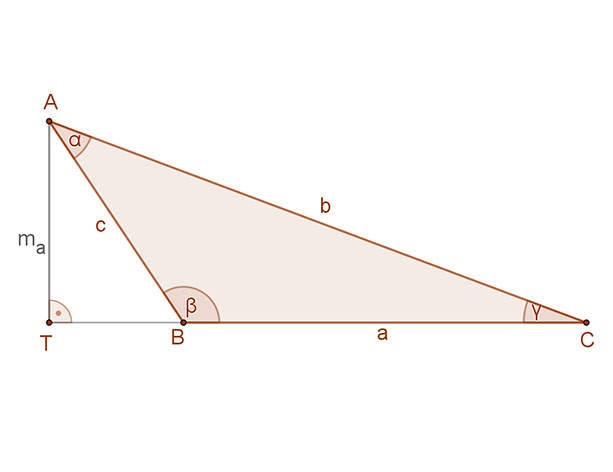
Ezekből az összefüggésekből kapjuk: a⋅c⋅sinβ=a⋅b⋅sinγ=b⋅c⋅sinα .
Az a⋅c⋅sinβ=b⋅c⋅sinα -ból „c„-vel egyszerűsítve: a⋅sinβ=b⋅sinα. Ezt aránypár alakba írva: a:b=sinα:sinβ.
Hasonlóan az a⋅c⋅sinβ=a⋅b⋅sinγ-ból „a„-val egyszerűsítve: c⋅sinβ=b⋅sinγ. Ezt aránypár alakba írva: b:c= sinβ:sinϒ.
A kapott összefüggéseket egy kifejezésbe írva kapjuk a szinusz tételt: a:b:c=sinα:sinβ:sinγ.
Szinusz tétel szavakkal:
Bármely háromszögben az oldalak aránya megegyezik a velük szemközti szögek szinuszának arányával.
A szinusz tétel jól alkalmazható a háromszög adatainak meghatározásában.
A szinusz tétel alkalmazható:
1. Ha ismerjük a háromszög bármely két szögét és egy oldalát, a szinusz tétel segítségével kiszámíthatjuk a háromszög hiányzó oldalait.
2. Ha ismerjük a háromszög két oldalát és a nagyobbik ismert oldallal szemben lévő szöget, a szinusz tétel segítségével kiszámíthatjuk a másik oldallal szembeni szöget.
3. Ha a kisebbik oldallal szembeni szög az ismert, akkor ezek az adatok nem egyértelműen határozzák meg a háromszöget. Nulla, egy vagy két megoldás is elképzelhető. (Nincs háromszög, derékszögű a háromszög, vagy egy hegyes és egy tompa szögű háromszög.) Itt mérlegelni kell a lehetőségeket.


Comments are closed, but trackbacks and pingbacks are open.