A számtani és mértani közép közötti összefüggés

Definíció:

Két nemnegatív szám számtani közepének a két szám összegének a felét nevezzük.

A számtani közepet szokás aritmetikai középnek is nevezni, és „A” betűvel jelölni.

Formulával:  ​\( A(a;b)=\frac{a+b}{2} \) , ahol a;b∈ℝ​; a≥0; b≥0.

Definíció:

Két nemnegatív szám mértani közepének a két szám szorzatának négyzetgyökét nevezzük.

A mértani közepet szokás geometria középnek is nevezni, és „G” betűvel jelölni.

Formulával: \( G(a;b)=\sqrt{a·b} \)​, ahol a;b∈ℝ​; a≥0; b≥0.

Állítás:

Két (nemnegatív) szám mértani közepe nem nagyobb, mint ugyanezen két szám számtani közepe.

Formulával:  ​\( \sqrt{a·b}≤\frac{a+b}{2} \)​

Bizonyítás:

Mivel az állítás mindkét oldalán nemnegatív kifejezés áll, ezért mindkét oldalát négyzetre emelhetjük, ez most ekvivalens átalakítás: ​\( a·b≤\frac{(a+b)^{2}}{4} \)​

A jobboldali kifejezésben a zárójel felbontása és a nevezővel történő átszorzás után:  4ab≤a²+2ab+b².

Az egyenlőtlenséget rendezve, azaz 0-ra redukálva: 0≤a²-2ab+b².

Így a jobb oldalon teljes négyzetet kaptunk: 0≤(a-b)² , amely mindig igaz.

Az egyenlőség akkor következik be, ha a két szám egyenlő: a=b

A számtani és mértani közép közötti összefüggést geometriai úton is szemléltethetjük.

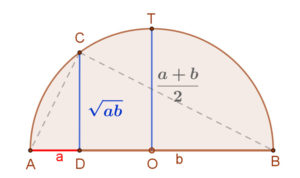Legyen adott két a illetve b hosszúságú szakasz. Vegyünk fel egy a+b=AB átmérőjű kört. Az a és b szakaszok D találkozási pontjában emeljünk merőlegest az AB átmérőre. Így kapjuk a C pontot. Thalesz tétele szerint az ABC háromszög derékszögű. Ebben az AB átfogóhoz tartozó CD magasság a magasság tétel értelmében mértani közepe az AB átfogó két szeletének, az a és b hosszúságú szakaszoknak. Ez a CD szakasz pedig nem lehet nagyobb a kör sugaránál, az OT szakasznál, amely a két szakasz számtani közepével egyenlő.

Hippokratész a kocka kettőzésének feladatát a  mértani középarányos meghatározására vezette vissza.