Tetszőleges szög tangense, kotangense

Tetszőleges szög tangensének és kotangensének meghatározásához felhasználjuk a tetszőleges szinuszára és koszinuszára vonatkozó definíciókat.

Definíció:

Tetszőleges szög tangense a szög szinuszának és koszinuszának hányadosával egyenlő.

Formulával: ​\( tgα=\frac{sinα}{cosα}, \; cosα≠0; \; α≠\frac{ π }{2}+k· π , \; k∈ℤ \)​.

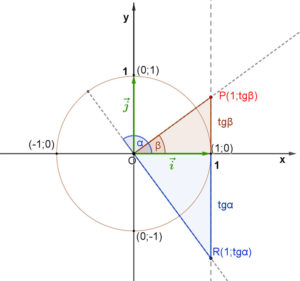A definíciónak geometriai értelmezést is tudunk adni.

Egy szög tangense, a koordinátasíkon annak a pontnak az y koordinátája, amelyet az adott szöggel elforgatott egységvektor egyenese az origó középpontú egységsugarú kör (1;0) pontjához húzott érintőből kimetsz.

Definíció:

Tetszőleges szög kotangense a szög koszinuszának és szinuszának hányadosával egyenlő.

Formulával: ​\( ctgα=\frac{cosα}{sinα}, \; sinα≠0; \; α≠0+k· π , \; k∈ℤ \)​.

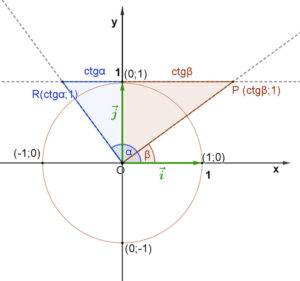A definíciónak geometriai értelmezést is tudunk adni:

Egy szög kotangense, a koordinátasíkon annak a pontnak az x koordinátája, amelyet az adott szöggel elforgatott egységvektor egyenese az origó középpontú egységsugarú kör (0;1) pontjához húzott érintőből kimetsz.

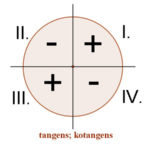
Mivel a tangens és a kotangens a szinusz és a koszinusz segítségével lett definiálva, ezért ezen szögfüggvények előjeleit az alábbi ábra szemlélteti:

Szög	Helyettesítő hegyesszög	Tangens előjele	Cotangens előjele
0°		0	Nincs értelmezve
0°<ß<90°		+	+
90°		Nincs értelmezve	0
90°<ß<180°	180°-ß	–	–
180°		0	Nincs értelmezve
180°<ß<270°	ß-180°	+	+
270°		Nincs értelmezve	0
270° <ß<360°	360° -ß	–	–
360°		0	Nincs értelmezve

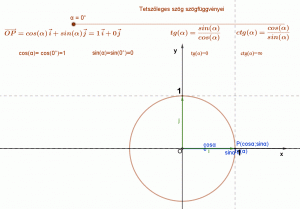
Az alábbi animáció szemlélteti a különböző szögfüggvények definícióit:A szögfüggvények  grafikonjait és jellemzésüket megtalálod itt: szinusz, koszinusz, tangens, kotangens.