Binomiális tétel kimondja, hogy kéttagú kifejezések pozitív egész kitevőjű hatványának rendezett polinom alakban történő felírásakor a következő kifejezéseket kapjuk:
Ha a és b tetszőleges valós számok és n pozitív egész szám, akkor: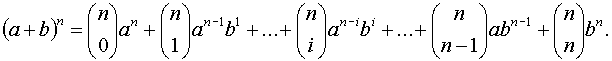
A tételben szereplő \( \binom{n}{k} \) együtthatókat binomiális együtthatóknak is nevezik.
Pascal francia matematikus 1654-ben (a +b)n binomiális együtthatókat tanulmányozta és módszert adott kiszámításukra.
| (a+b)0 | = | 1 | = | \( \binom{0}{0} \) |
| (a+b)1 | = | a+b | = | \( \binom{1}{0} \)a+\( \binom{1}{1} \)b |
| (a+b)2 | = | a2+2ab+b2 | = | \( \binom{2}{0} \)a+ \( \binom{2}{1} \)ab+ \( \binom{2}{2} \)b2 |
| (a+b)3 | = | a3+3a2b+3ab2+b3 | = | \( \binom{3}{0} \)a3+\( \binom{3}{1} \)a2b+\( \binom{3}{2} \)ab2+\( \binom{3}{3} \)b3 |
Rendezzük el a binomiális együtthatókat egy táblázatban:
| \( \binom{0}{0} \) | ||||||||||
| \( \binom{1}{0} \) | \( \binom{1}{1} \) | |||||||||
| \( \binom{2}{0} \) | \( \binom{2}{1} \) | \( \binom{2}{2} \) | ||||||||
| \( \binom{3}{0} \) | \( \binom{3}{1} \) | \( \binom{3}{2} \) | \( \binom{3}{3} \) | |||||||
| \( \binom{4}{0} \) | \( \binom{4}{1} \) | \( \binom{4}{2} \) | \( \binom{4}{3} \) | \( \binom{4}{4} \) | ||||||
| \( \binom{5}{0} \) | \( \binom{5}{1} \) | \( \binom{5}{2} \) | \( \binom{5}{3} \) | \( \binom{5}{4} \) | \( \binom{5}{5} \) |

És így tovább.
Most helyezzük el a binomiális együtthatók értékeit egy hasonló táblázatba:
A binomiális együtthatóknak ezt az elrendezését nevezzük Pascal háromszögnek.
A háromszög minden sora 1-gyel kezdődik, és 1-gyel végződik.
Ebben a háromszög elrendezésben a 2. sortól kezdve a sorok bármely belső száma a felette lévő sorban balról és jobbról álló két számnak az összege.
Így nagyon gyorsan ki lehet tölteni a következő sort, amely a következő binom polinom alakjához használható:
(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6.
Az előbb megfigyelt összefüggés általánosan felírva:
\( \binom{n}{k} \)+\( \binom{n}{k+1} \)=\( \binom{n+1}{k+1} \)


Comments are closed, but trackbacks and pingbacks are open.