Nézzük meg a kéttagú kifejezések pozitív egész kitevőjű hatványának rendezett polinom alakban történő felírásakor kapott kifejezéseket!
(a+b)2=a2+2ab+b2.
(a+b)3=a3+3a2b+3ab2+b3.
(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
Ezeket a polinomokat a hatványozás elvégzésével, és az összevonásokkal viszonylag könnyen meg tudtuk kapni.
Ha azonban egy kicsit általánosabban próbáljuk ezt problémát megközelíteni, akkor a kérdés úgy vethető fel, hogyan írható rendezett polinom alakban az (a+b)n kifejezés? Az egyes tagokban milyen változók milyen kitevőkön fordulnak elő, és a tagokban milyen együtthatók szerepelnek?
Változóként most az „a” és a „b” használjuk. A kitevők és az együtthatók meghatározása kombinatorikai meggondolásokat igényel.
Nézzük az (a+b)5 kifejezést, amely szorzatként kiírva:
(a+b)5=(a+b)⋅(a+b)⋅(a+b)⋅(a+b)⋅(a+b)
A tényezők a és b tagjai közül minden lehetséges módon össze kell szorozni egyet-egyet. Az így kapott egyes tagokat és a bennük szereplő változók kitevőit az alábbi meggondolással lehet meghatározni:
Ha minden tényezőből az a-t választjuk: a5.
Ha a-t négy tényezőből, b-t egyből: a4b.
Ha a-t háromból, b-t pedig kettőből: a3b2.
Ha a-t két tényezőből, b-t pedig háromból: a2b3.
Ha a-t egy tényezőből, a b-t pedig négyből: ab4.
Ha minden tényezőből b-t választjuk: b5.
Az a5, a4b, a3b2, a2b3, ab4, b5 tagok együtthatói azok a számok, amelyek megadják, hogy az 5 tényezőből hányféleképpen lehet kiválasztani azokat a tényezőket, amelyek a megfelelő számú (kitevőjű) b tényezőt adják. Ezek az együtthatók tehát 5-nek megfelelő számú kombinációja lesz. Ennek megfelelően:
| Az a5 tag együtthatója 5-nek 0-ad fokú kombinációja: | \( \binom{5}{0} \) | = | 1 |
| Az a4b tag együtthatója 5-nek első fokú kombinációja. | \( \binom{5}{1} \) | = | 5 |
| Az a3b2 együtthatója 5-nek 2-od fokú kombinációja | \( \binom{5}{2} \) | = | 10 |
| Az a2b3 együtthatója 5-nek 3-ad fokú kombinációja | \( \binom{5}{2} \) | = | 10 |
| Az ab4 együtthatója 5-nek 4-ed fokú kombinációja. | \( \binom{5}{4} \) | = | 5 |
| Az b5 együtthatója 5-nek 5-öd fokú kombinációja. | \( \binom{5}{5} \) | = | 1 |
Tehát:
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
Tétel:
Ha a és b tetszőleges valós számok és n pozitív egész szám, akkor:
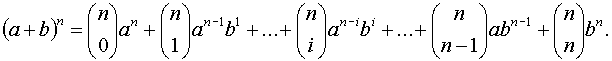
A tételben szereplő \( \binom{n}{k} \)együtthatókat binomiális együtthatóknak is nevezik.
A fenti meggondolások és számítások azt sejtetik, hogy a tétel állítása igaz.
A tétel bizonyítása továbbiakban teljes indukcióval lenne lehetséges, amelytől itt most eltekintünk.
A binomiális tételben szereplő polinom n+1 tagú. Az ilyen sok tagból álló összeg leírására a matematikában egy rövidebb jelölést használnak.
A binomiális tétel rövidebb alakja: \( {{\left(a+b\right)}}^n=\sum_{i=0}^{n} \binom{n}{i}{a^{n-i}b^{i}} . \) Az ebben szereplő Σ szimbólum, a görög abc szigma betűje jelöli az összegzés műveletét. A binomiális tétel Newton nevéhez kötődik.
Pascal francia matematikus 1654-ben (a +b)n binomiális együtthatókat tanulmányozta és a Pascal háromszöggel módszert adott kiszámításukra.


Comments are closed, but trackbacks and pingbacks are open.