Azonosságok:
1. Kéttagú összeg illetve különbség négyzete.
2. Két tag különbségének és összegének a szorzata.
3. Háromtagú összeg négyzete.
4. Kéttagú összeg illetve különbség harmadik hatványa.
5. Két tag köbének összege és különbsége.
1. Kéttagú összeg ill. különbség négyzete.
Szavakkal: Egy kéttagú kifejezés négyzete egyenlő az első tag négyzetének, az első és második tag előjeles szorzatának kétszeresének és a második tag négyzetének összegével.
Formulával: (a+b)2=a2+2ab+b2. (Szorzat alak, összeg alak.)
Példa: \( \left(3x±\frac{2}{5}y\right)^2=9x^2±\frac{12}{5}xy+\frac{4}{25}y^2 \)
2. Két tag különbségének és összegének a szorzata.
Szavakkal: Két tag összegének és különbségének szorzata egyenlő a két tag négyzetének különbségével.
Formulával: (a+b)(a-b)=a2-b2. (Szorzat alak, összeg alak.)
Példa: \( \left(\frac{2}{3}x+7y \right)\left(\frac{2}{3}x-7y\right)=\left(\frac{2}{3}x \right) ^2-(7y)^2=\frac{4}{9}x^2-49y^2 \)
3. Háromtagú összeg négyzete.
Szavakkal: Egy háromtagú összeg négyzete egyenlő a tagok négyzeteinek és a lehetséges kétszeres szorzataiknak összegével.
Formulával: (a+b+c)2=a2+b2+c2+2ab+2ac+2bc. (Szorzat alak, összeg alak.)
4. Kéttagú összeg illetve különbség harmadik hatványa.
Formulával: (Szorzat alak, összeg alak.)
(a+b)3=a3+3a2b+3ab2+b3
(a-b)3=a3-3a2b+3ab2-b3
Megjegyzés: Két tag összegének (ill. különbségének) tetszőleges pozitív egész kitevőjű hatványára, azaz kifejezésre vonatkozó általános összefüggést a binomiális tétel tartalmazza.
5. Két tag köbének összege és különbsége.
Formulával: (Szorzat alak, összeg alak.)
(a+b)(a2-ab+b2)=a3+b3
(a-b)(a2+ab+b2)=a3-b3
Alkalmazás
- Algebrai törtekkel végzett műveleteknél. Egyszerűsítés, közös nevezőre hozás.
- Törtek gyöktelenítése.
Feladat:
| Végezzük el a következő műveleteket a következő algebrai kifejezésben! | 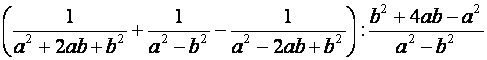 |
(Összefoglaló feladatgyűjtemény 288. feladat.)
Megoldás:
| Alakítsuk szorzattá amit lehet a fenti azonosságok segítségével: | 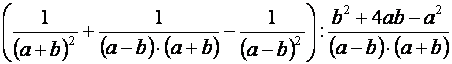 |
| Most már az értelmezési tartományt is könnyebb meghatározni! | a,b∈ℝ; |a|≠|b|; b2+4ab-a2≠0 |
| Az első zárójelben szereplő törtek közös nevezője: | (a+b)2⋅(a-b)2 |
| A közös nevezőre hozás után: | 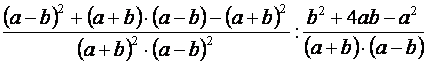 |
| Az első tört számlálójában felbontjuk a zárójeleket: | 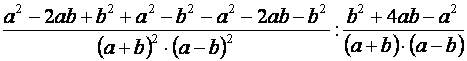 |
| Az első tört számlálójában elvégezzük a lehetséges összevonásokat: | 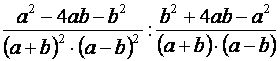 |
| Az osztó tört reciprokával szorzunk: | 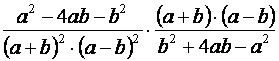 |
| Észrevehetjük, hogy a második tört nevezője az első tört számlálójának az ellentettje: | 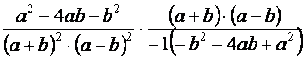 |
| Elvégezzük a lehetséges egyszerűsítéseket: | 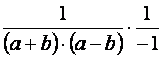 |
| Tehát a végeredmény: | 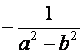 |


Comments are closed, but trackbacks and pingbacks are open.