Négyszögek osztályozása

Nevezetes (speciális) négyszögek.

1. Trapézok: Olyan négyszögek, amelyeknek van két párhuzamos oldala.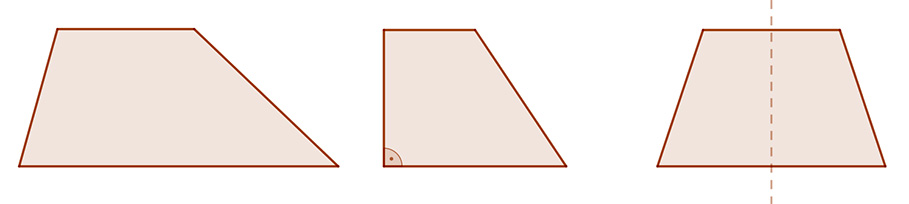

2. Paralelogrammák: Olyan négyszögek, amelyeknek szemközti oldalai párhuzamosak.

 

3. Téglalapok: Olyan négyszögek, amelyeknek egyenlők a szögei.

4. Rombuszok:  Olyan négyszögek, amelyeknek egyenlők az oldalai.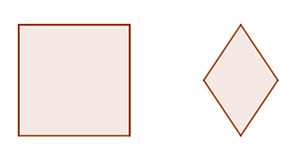5. Négyzetek: Olyan négyszögek, amelyeknek szögei és az oldalai is egyenlők.6. Deltoidok:  Olyan négyszögek, amelyeknek van csúcsai átmenő szimmetriatengelye.

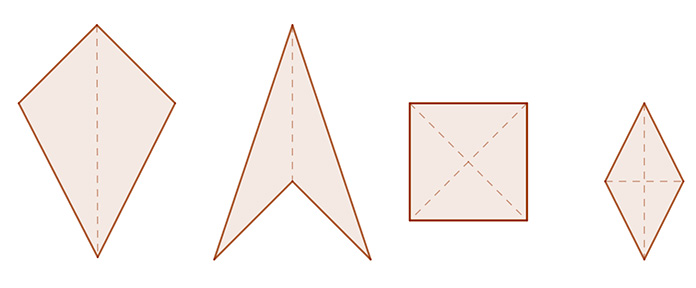
Négyszögek osztályozása.

A. Az oldalak párhuzamossága szerint 3 nagy csoportba sorolhatók a négyszögek.

1. Két-két párhuzamos oldaluk van. Ez a paralelogrammák családja. A téglalap, a rombusz és a négyzet is ide tartozik.

2. Két párhuzamos oldaluk van. A trapézok családja, amelynek részhalmaza a paralelogrammák családja.

3. Nincs párhuzamos oldaluk. A fent említett speciális négyszögek közül bizonyos deltoidok tartozhatnak ide.

B. Az oldalak egyenlősége szerint 5 csoportba sorolhatók.

1. Minden oldaluk egyenlő: rombuszok, és ezen belül a négyzetek.

2. Két-két szemközti oldaluk egyenlők. Ezek a paralelogrammák.

3. Szomszédos oldalaik egyenlők. Ezek a deltoidok. A deltoidok családjának részhalmaza a rombuszok és a négyzetek családja.

4. Két vagy három egyenlő oldala van. A speciális négyszögek közül csak a trapézok között fordulhat ilyen elő.

5. Nincs egyenlő oldaluk. Az általános négyszögeken kívül a trapéz lehet ilyen.

Nézzük ezután hogyan csoportosíthatók a speciális négyszögek:

A mellékelt halmazábrán láthatók az egyes speciális négyszögek csoportosítva.

A={Általános négyszögek}
T={Trapézok}
P={Paralelogrammák}
L={Téglalapok}
R={Rombuszok}
N={Négyzetek}
D={Deltoidok}

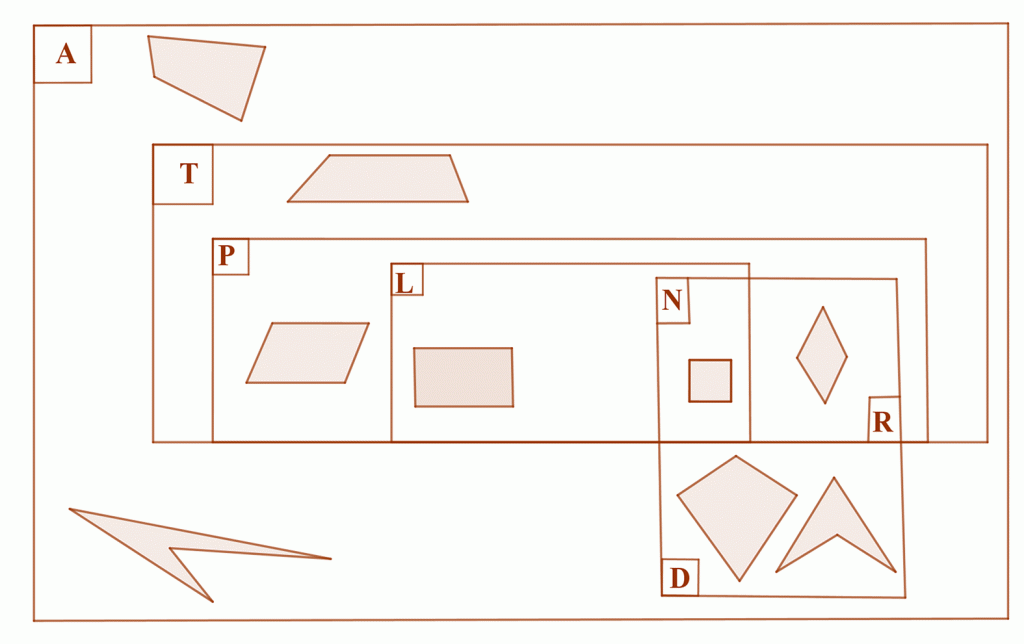
Az egyes halmazok között kapcsolatok tehát:
P⊂T; L⊂P; R⊂P; N⊂L; N⊂R; R⊂D; N⊂D. (⊂: valódi részhalmaz)
L∩R=N (∩: Halmazok metszete.)

Feladat:

Az alábbi állítások közül melyek igazak, és miért

(Összefoglaló feladatgyűjtemény 1743. feladat.)

a. Minden rombusz érintőnégyszög.
b. Minden érintőnégyszög trapéz.
c. Minden téglalap trapéz.
d. Van olyan trapéz, amelyik húrnégyszög.

Megoldás:

a) Minden rombusz érintőnégyszög.

Ez igaz, mivel a rombusz oldalai egyenlő hosszúak, ezért szemközti oldalainak összege mindig egyenlő. Tehát minden rombusz érintőnégyszög.

b) Minden érintőnégyszög trapéz.

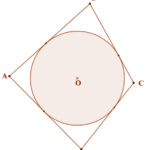Ez nem igaz, mert lehet egy kör köré úgy 4 darab érintőt húzni, hogy azok között ne legyen párhuzamos. Például:

 

c) Minden téglalap trapéz.

Ez igaz, hiszen a téglalapnak vannak párhuzamos oldalai.

d) Van olyan trapéz, amelyik húrnégyszög.

Ez igaz, mert a szimmetrikus trapéz szemközti szögei egymást 180°-ra egészítik ki.