Halmazok kölcsönös helyzete

Diszjunkt halmaz, részhalmaz; komplementer halmaz

Két halmaz kölcsönös helyzetével kapcsolatban három lehetőség áll fenn:

1. Két halmaznak nincs közös eleme.
2. Az egyik halmaz tartalmazza a másik halmaz minden elemét.
3. Két halmaznak van közös, de van nem közös eleme is.

1. Két halmaznak nincs közös eleme.

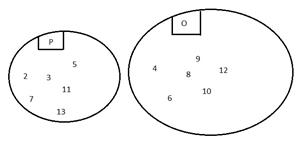
Jelöljük „P”–val a prímszámok halmazát és legyen „O” az összetett számok halmaza.
Azaz: P={Prímszámok} = {2; 3; 5; 7; 11; 13;…}
illetve O={Összetett számok} = {4; 6; 8; 9; 10; 12;…}
Természetesen ennek a két halmaznak nincs közös eleme.

 Definíció:

Ha két halmaznak nincs közös eleme, akkor a két halmazt (egymáshoz viszonyítva) diszjunktnak nevezzük.
Ez a fogalom kettőnél több halmaz esetén is értelmezhető.

2. Az egyik halmaz tartalmazza a másik halmaz minden elemét.

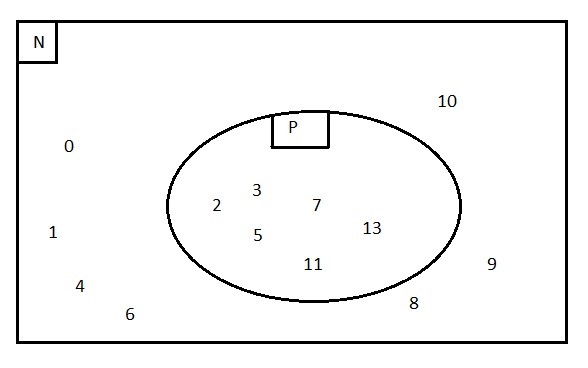
A szokásos jelöléssel jelöljük „ℕ”-nel az egész számok halmazát és továbbra is  „P”-vel a prímszámok halmazát.
Azaz: ℕ={Természetes számok} = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13;…}
illetve P={Prímszámok} = {2; 3; 5; 7; 11; 13;…}

Tudjuk, minden prímszám természetes szám, de nem minden természetes szám prím, mivel az összetett számok és a 0 valamint az 1 nem prímszám.
Tehát a „P” halmaz minden eleme része (eleme) az „ℕ” halmaznak is.

Definíció:

Egy  „A” halmaz részhalmaza „B„-nek, ha A minden eleme a B halmaznak is eleme.
Röviden: A⊆B , ha a∈A, akkor a∈B.

Definíció:

Az A halmaz valódi részhalmaza B-nek, ha A részhalmaza a B halmaznak, de nem egyenlő vele.
Röviden: A⊂ B, ha A ⊆ B, és A ≠ B. A fenti példában: P⊂ N, mert P≠N

Példa:

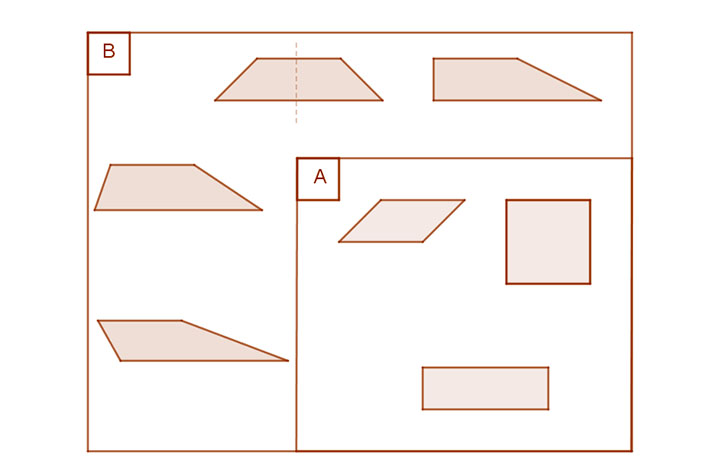Legyen A={Paralelogrammák}, B={Trapézok}

Nézzük ezeknek a négyszögeknek a definícióit!

A: Paralelogramma olyan négyszög, amelynek szembelévő oldalai párhuzamosak.
B: Trapéz olyan négyszög, amelynek van két párhuzamos oldala.

A definíciókból következik, hogy minden paralelogramma egyben trapéz is, ugyanakkor van olyan trapéz, amelyik nem paralelogramma.
A paralelogrammák halmaza tehát valódi részhalmaza a trapézok halmazának. (A ⊂ B)

Komplementer (kiegészítő) halmaz:

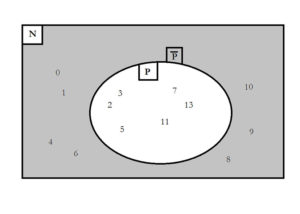A szokásos jelöléssel jelöljük „ℕ”-nel a természetes számok halmazát és továbbra is; „P”-vel a prímszámok halmazát.
Azaz: ℕ={Természetes számok} = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13;…}
illetve P={Prímszámok} = {2; 3; 5; 7; 11; 13;…}
A prímszámok halmaza a 0, az 1 és az összetett számokkal kiegészítve a természetes számok halmazát adja.
Az összetett számok a 0 és az 1 számmal együtt a prímszámok kiegészítő halmaza a természetes számokra nézve.

Ha egy A halmaz részhalmaza egy másik halmaznak, akkor szokás ezt az A-t tartalmazó halmazt alaphalmaznak (univerzum halmaznak) is nevezni. Ennek szokott jele: „U” halmaz.

Definíció:

Egy A halmaz komplementerhalmazának (kiegészítő halmazának) nevezzük az alaphalmaz azon elemeinek a halmazát, amelyek nem elemei az „A” halmaznak.
Jelölés: A komplementer halmaz jelölésére a legáltalánosabb jelölés a felülvonás.

Azaz: ​\( \overline{A} \)​ jelöli az „A” halmaznak az alaphalmazra (univerzum halmazra) vonatkozó komplementer (kiegészítő) halmazát.
A kiegészítő halmaz fogalma tehát egy viszony. Fontos hangsúlyozni, hogy mi adott esetben az alaphalmaz.

Például:

Legyen „ℝ” a valós, „ℚ” a racionális számok halmaza. Ebben az esetben a racionális számok komplementer halmaza a valós számok halmazára vonatkoztatva a ℚ*-gal jelölt irracionális számok halmaza.

Ha az alaphalmaz az egész számok halmaza, akkor a természetes számok komplementer halmaza az egész számok halmazára vonatkoztatva a negatív egész számok. Azaz \( \overline{ℕ} \)​=ℤ^– .

A paralelogrammák kiegészítő halmaza a négyszögek halmazára nézve azok a négyszögek, amelyeknek nincs párhuzamos oldala.

3. Két halmaznak van közös, de van nem közös eleme is.

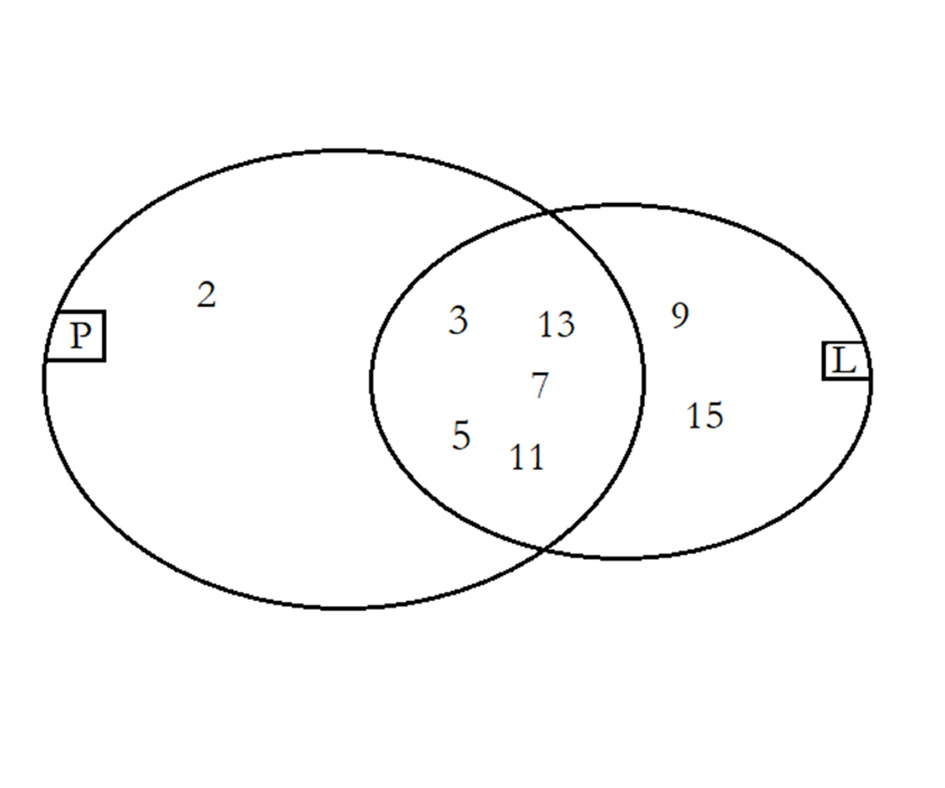Jelöljük „P”–vel a prímszámok halmazát és legyen „L” a páratlan számok halmaza.
Azaz: P={Prímszámok} = {2; 3; 5; 7; 11; 13;…}
illetve L={Páratlan számok} = {3; 5; 7; 9; 11; 13; 15;…}
Ennek a két halmaznak van közös eleme, de van nem közös eleme is.
Van olyan prímszám, ami nem páratlan nevezetesen a „2”, az egyetlen páros prímszám és van olyan páratlan szám, amelyik nem prímszám.