Halmazműveletek

1. Két halmaz egyesítése

Definíció:

Két halmaz uniójának (egyesítésének, összegének) nevezzük azoknak az elemeknek a halmazát, amelyek a két halmaz közül legalább az egyiknek az elemei.
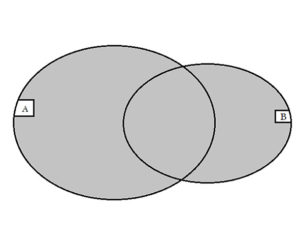Jelölés: A és B halmazok uniójának jele: A∪B. Röviden: c ∈ A∪B, ha c ∈ A vagy c ∈ B.

Ábrázolása: Ezt a műveletet a Venn diagram segítségével a következőképpen tudjuk szemléltetni:

A ∪ A = A. Bármely halmaz önmagával való uniója önmaga.
A ∪ ∅= A. Bármely halmaznak az üres halmazzal való uniója önmaga.
A ∪ B = B ∪ A. Kommutatív (felcserélhető) tulajdonság.
A ∪ B ∪ C = (A  ∪ B) ∪ C = A  ∪ (B ∪  C). Asszociatív (csoportosítható) tulajdonság.

2. Két halmaz közös része

Definíció:

Két halmaz metszetének (közös részének, szorzatának) nevezzük azoknak az elemeknek a halmazát, amelyek mindkét halmaznak az elemei.
Jelölés: A és B halmazok metszetének: A∩B.Röviden: c ∈ A ∩ B, ha c ∈ A és c ∈ B.

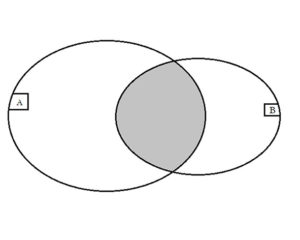Ábrázolása: Ezt a műveletet a Venn diagram segítségével a következőképpen tudjuk szemléltetni:

A ∩ A = A Bármely halmaz önmagával való metszete önmaga.
A ∩∅ =∅. Bármely halmaznak az üres halmazzal való metszete az üres halmaz.
A ∩ B=B ∩A. Kommutatív tulajdonság. (Felcserélhető.)
A ∩ B∩ C = (A ∩ B) ∩ C = A ∩ ( B ∩ C). Asszociatív tulajdonság. (Csoportosítható.)

Diszjunkt  halmazok metszete üres halmaz.

Halmazok metszetére és egyesítésére vonatkozóan igaz a disztributív tulajdonság a következő módon:

1. Halmazok uniója (egyesítése) disztributív a halmazok metszetre nézve:  A∪(B∩C)=(A∪B)∩(A∪C)
2. Halmazok metszete disztributív a halmazok egyesítésére (uniójára) nézve. A∩(B∪C)=(A∩B)∪(A∩C)

3. Halmazok különbsége

Definíció:

Az A és B halmaz (ebben a sorrendben tekintett) különbségének nevezzük azoknak az elemeknek a halmazát, amelyek elemei az A halmaznak és nem elemei a B halmaznak.
Jelölés: A és B halmazok különbsége: A\B. Röviden: c ∈ A\B, ha c ∈ A és c ∉B.

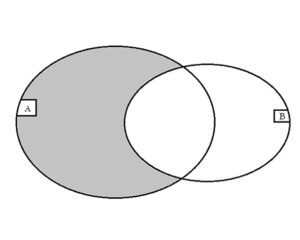Ábrázolása: Ezt a műveletet a Venn diagram segítségével a következőképpen tudjuk szemléltetni:

A\A =∅. Bármely halmazból önmagát kivonva az üres halmazt kapjuk.
A\∅ = A. Bármely halmazból az üres halmazt kivonva az eredeti halmazt kapjuk.
A\B ≠ B\A. A halmazok kivonása nem kommutatív.
(A\B)\C ≠ A\( B\C). A halmazok kivonása nem asszociatív.

Komplementer halmaz

Definíció

Legyen az U-val jelölt alaphalmaz egy részhalmaza az A halmaz. (A⊆U)Ebben az esetben: U\A=​\( \overline{A} \)​   

Szavakkal: Az alaphalmaz és részhalmazának különbsége a részhalmaz komplementer halmaza az alaphalmazra vonatkoztatva.

Halmazok metszetére, egyesítésére és a komplementer-képzésre vonatkozóan igazak az un. de Morgan azonosságok:

1. Két halmaz komplementerének egyesítése megegyezik a két halmaz metszetének komplementerével: ​\( \overline{A}∪\overline{B}=\overline{A∩B} \)​
2. Két halmaz komplementerének metszete megegyezik a két halmaz egyesítésének komplementerével: ​\( \overline{A}∩\overline{B}=\overline{A∪B} \)​

A halmazműveletek tulajdonságainak összefoglalása:

• A halmazműveletek közül kommutatív és asszociatív a halmazok uniója, és metszete.
• Két halmaz különbsége nem kommutatív és nem asszociatív.
• Halmazok metszetére és egyesítésére vonatkozóan igaz a disztributív tulajdonság
• A halmazműveletekre is igazak az un. de Morgan azonosságok

Nézzük meg a halmazműveleteket egy nagyon egyszerű példán!

Feladat:

Határozza meg az A és B halmazokat, ha tudja, hogy A ∪ B ={1;2;3;4;5}; A ∩ B ={3;5}; A\B={1}; B\A={2;4}

(Összefoglaló feladatgyűjtemény 205. feladat.)

Megoldás:

Mivel az A∩ B ={3; 5}, ezért a 3 és az 5 eleme az A-nak. Az A\B={1} feltétel miatt pedig az 1-es szám is eleme az A-nak. Tehát eddig A={1; 3; 5}.

Mivel az A ∩ B ={3; 5}, ezért a 3 és az 5 eleme a B-nek is. A B\A={2; 4} feltétel miatt pedig a 2-es és a 4-es szám is eleme a B-nek. Tehát eddig B={3; 5; 2; 4}.

Mivel az így kapott A és B halmazok uniója megegyezik a megadottal: A ∪B={1; 2; 3; 4; 5} halmazzal, ezért a végeredmény:
A={1; 3; 5} és B={2; 3; 4; 5} lehet csak.
Venn diagram segítségével rajzon is megoldhatjuk a feladatot!

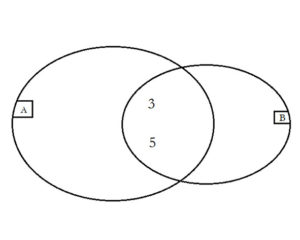Először A∩B ={3;5}feltételt használjuk fel. Az A∩B halmaz elemei mindkét halmazhoz hozzátartoznak, tehát a két halmaz közös részéhez írjuk őket.

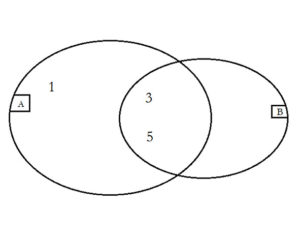
Most az A\B={1} feltételt használjuk fel. Ez azt jelenti, hogy az 1-es szám csak az A halmazhoz tartozik, de a B-hez nem.

 

 

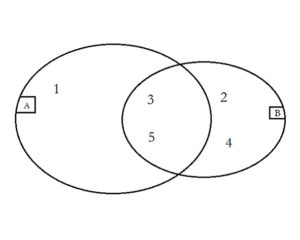
Végül a B\A={2;4}feltétel felhasználásával:

 

 

 

 

 

A végeredmény a Venn diagramról könnyedén leolvasható:

A={1; 3; 5} és B={2; 3; 4; 5}.