A határozott integrál illetve a Newton-Leibniz formula segítségével meg tudjuk határozni egy integrálható függvény és az „x” tengely által közbezárt síkidom területét.
Ez az alapja annak is, hogy két függvény által közrefogott terület értékét is k tudjuk számítani.
 Példa:
Példa:
Határozzuk meg az g: ℝ\ℝ–→ℝ, g(x)=\( \sqrt{2x} \) gyökfüggvény és az l(x)=x/3+4/3 lineáris függvény által közrefogott terület nagyságát!
Megoldás:
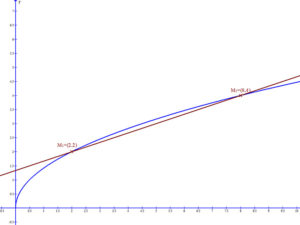 Első lépésként meg kell határozni a két függvény metszéspontjait. Ez a két függvény szabálya által meghatározott egyenlet megoldását kívánja meg.
Első lépésként meg kell határozni a két függvény metszéspontjait. Ez a két függvény szabálya által meghatározott egyenlet megoldását kívánja meg.
Az egyenlet: \( \sqrt{2x}=\frac{1}{3}·x+\frac{4}{3} \). Ennek értelmezési tartománya: x∈ℝ\ℝ–. Átszorozva hárommal, majd mindkét oldalt négyzetre emelve egy másodfokú egyenletet kapunk: x2-10x+16=0. Ennek megoldásai: x1=2 és x2=8. Így a metszéspontok: M1=(2,2) és M2=(8,4).
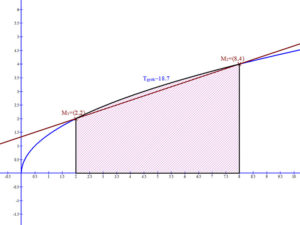 Második lépésként meghatározzuk a függvények alatti területeket a [2;8] intervallumon.
Második lépésként meghatározzuk a függvények alatti területeket a [2;8] intervallumon.
A gyökfüggvény esetén a Newton-Leibniz formula segítségével:
A \( \int_{2}^{8}{ \sqrt{2x}dx} \) alól \( \sqrt{2} \) kiemelve az \( \sqrt{2}\int_{2}^{8}{\sqrt{x}dx } \) integrál értékét kell kiszámítani.
Mivel a \( \sqrt{x}=x^{\frac{1}{2}} \) függvény primitív függvénye F(x)=\( \frac{2}{3}x^{\frac{3}{2}} \), ezért:
\[ \int_{2}^{8}{ \sqrt{2x}dx}=\sqrt{2}\int_{2}^{8}{\sqrt{x}dx }=\sqrt{2}·\left [F(x) \right ]_{2}^{8}=\sqrt{2}·\left [\frac{2}{3}·x^{\frac{3}{2}} \right ]_{2}^{8}=\sqrt{2}·\left(F(8)-F(2) \right) \]
Így:
\[ \int_{2}^{8}{ \sqrt{2x}dx}= \sqrt{2}·\left(\frac{2}{3}·8^{\frac{3}{2}}-\frac{2}{3}·2^{\frac{3}{2}} \right) =\frac{56}{3}=18.\dot{6} \]
Tehát a gyökfüggvény alatti terület: Tgyök=56/3 területegység.
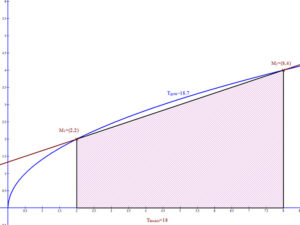 A lineáris függvény esetén felesleges az integrál alkalmazása.
A lineáris függvény esetén felesleges az integrál alkalmazása.
A függvény alatti terület ebben esetben egy trapéz, amelynek területe: \( T_{lineáris}=T_{trapéz}=\frac{(2+4)·6}{2}=18 \).
Tehát a lineáris függvény alatti terület: Tlineáris=18 területegység.
Harmadik lépésként a két terület különbsége adja meg a két függvény által közrefogott területet.
Az eredmény: Tközrefogott=Tgyök-Tlineáris=2/3 területegység.
Összefoglalva:
Két integrálható függvény által közrefogott terület kiszámítása 3 lépésből áll.
- A függvények metszéspontjainak meghatározása. Ez leggyakrabban egyenlet megoldást jelent.
- Az egyes függvények alatti területek meghatározása. Általában a Newton-Leibniz formula segítségével
- A területek különbsége a közrefogott terület mértéke.
Feladat: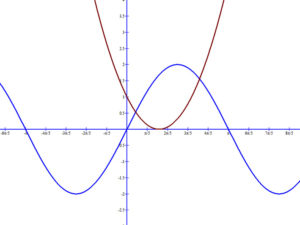
Határozzuk meg az s(x)=2sin(x) és a p(x)=(x-1)2 függvények által közrefogott terület nagyságát!
Megoldás:
Első lépésként meg kell határozni a két függvény metszéspontjait. Ez a két függvény szabálya által meghatározott egyenlet megoldását kívánna meg.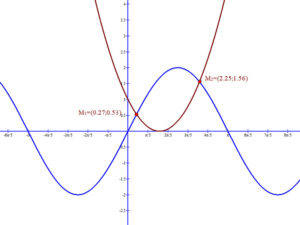
De a 2⋅sin(x)=(x-1)2 egyenlet megoldása nem egyszerű feladat. Itt segíthet a számítástechnika illetve valamilyen közelítő eljárás.
A metszéspontok: M1(0.27; 0.53) és M2(2.25; 1.56). Az integrálást tehát a [0.27; 2.25] intervallumon kell elvégezni.
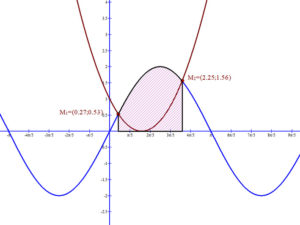 Második lépésként meghatározzuk a függvények alatti területeket a a Newton-Leibniz formula segítségével a [0.27;2.25] intervallumon.
Második lépésként meghatározzuk a függvények alatti területeket a a Newton-Leibniz formula segítségével a [0.27;2.25] intervallumon.
A 2⋅sin(x) függvény görbe alatti terület meghatározása a \( \int_{0.27}^{2.25}{2⋅sin(x)dx } \) integrál kiszámításával.
Az f(x)=2⋅sin(x) primitív függvénye: F(x)=-2⋅cos(x).
Az integrál:
\[ \int_{0.27}^{2.25}{2·sin(x)dx }=2·\left [F(x) \right ]_{0.27}^{2.25}=-2·\left(F(0.27)-F(2.25) \right) \]
Így tehát az integrál értéke:
\[ -2\left(cos(2.25)-cos(0.27) \right) ≈-2(-0.6282-0.9638)≈-2(-1.592)≈3.18 \]
Tehát a sin(2x) függvény alatti terület a [0.27;2.25] intervallumon: Ts≈3.18 területegység.
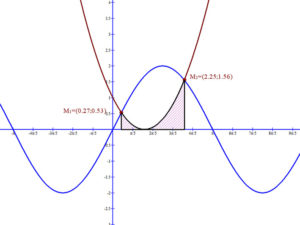 A p(x)=(x-1)2=x2-2x+1 függvény görbe alatti terület meghatározása az \( \int_{0.27}^{2.25}{(x-1)^{2}dx }=\int_{0.27}^{2.25}{(x^{2}-2x+1)dx } \) integrál segítségével.
A p(x)=(x-1)2=x2-2x+1 függvény görbe alatti terület meghatározása az \( \int_{0.27}^{2.25}{(x-1)^{2}dx }=\int_{0.27}^{2.25}{(x^{2}-2x+1)dx } \) integrál segítségével.
A p(x)=(x-1)2=x2-2x+1 függvény primitív függvénye: \( P(x)=\frac{x^{3}}{3}-x^{2}+x \).
Az integrál:
\[ \int_{0.27}^{2.25}{(x^{2}-2x+1)dx }=\left [P(x) \right ]_{0.27}^{2.25}=-2·\left(P(2.25)-P(0.27) \right) \]
Így tehát az integrál értéke:
\[ \left [P(x) \right ]_{0.27}^{2.25}≈\left [\frac{x^{3}}{3}-x^{2}+x \right ]_{0.27}^{2.25}≈(0.984-0.204≈0.78 \]
Tehát a p(x)=(x-1)2=x2-2x+1 f függvény alatti terület a [0.27;2.25] intervallumon: Tp≈0.78 területegység.
Harmadik lépésként a két terület különbsége adja meg a két függvény által közrefogott területet.
Az eredmény: Tközrefogott=Ts-Tp≈2.4 területegység.


Comments are closed, but trackbacks and pingbacks are open.