Feladat
Ábrázoljuk az f(x)=2x+3 függvényt és határozzuk meg az [1; 4] intervallumon a függvény alatti terület értékét!
Megoldás: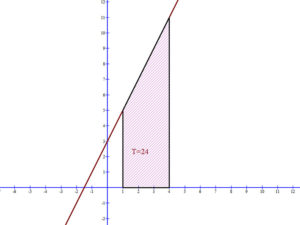
A függvény grafikonja:
Ez egy lineáris függvény. Az „x” tengely [1,4] intervalluma és a függvény közötti síkidom egy trapéz, amelynek párhuzamos oldalai: f(1)=5, f(4)=11 és a két párhuzamos oldal távolsága az intervallum hossza, a trapéz magassága=3 egység. Így a trapéz területe 24 területegység.
A határozott integrál definíciója szerint ez azt jelenti, hogy \( \int_{1}^{4}{\left(2x+3\right)dx}=24 \).
Az f(x)=2x+3 függvény primitív függvénye: F(x)=x2+3x+c. Hiszen, ha ezt a másodfokú függvényt deriváljuk: (x2+3x+c)’=2x+3=f(x) lesz az eredmény.
Számítsuk ki a primitív függvény értékét (c=0 esetén) a x=4 és az x=1 helyen!
F(4)=42+3⋅4=16+12=28 és F(1)=12+3⋅1=1+3=4.
F(4)-F(1)=28-4=24.
A két érték különbsége éppen a f(x)=2x+3 függvény alatti területet adja a [1;4] intervallumban.
\( \int_{1}^{4}{\left(2x+3\right)dx}=F(4)-F(1)=24 \).
Ez az eredmény nem véletlen.
Tétel:
Legyen az „f” függvény integrálható az [a; b] intervallumon. Ha az „f” függvénynek létezik az „F” primitív függvénye, akkor \( \int_{a}^{b}{f(x)dx }=F(b)-F(a) \).
Szokásos jelölés még: \( \int_{a}^{b}{f(x)dx }=\left [F(x) \right ]_{a}^{b} \).
Ez az un. Newton–Leibniz képlet (formula). Ennek a formulának természetesen nem a lineáris függvények esetén van jelentősége.
Ez a képlet az integrálható függvények görbéi és az „x” tengely által maghatározott síkidomok területének kiszámítását teszi lehetővé.
Bizonyítás:
A Newton-Leibniz tétel szerint egy folytonos függvény integrálfüggvénye a primitív függvényével egyenlő: \( \int_{a}^{x}{f(t)dt }=F(x)+c \).
Itt „c” állandó. Ha x=a, akkor \( \int_{a}^{a}{f(t)dt }=F(a)+c \)=0. Az F(a)+c=0 összefüggésből következik, hogy c=-F(a).
Legyen x=b. Ekkor \( \int_{a}^{b}{f(t)dt }=F(a)-f(a) \).
Ezt kellett bizonyítani.
Példák:
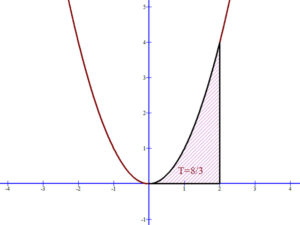
1. Számítsuk ki a Newton-Leibniz képlet segítségével az f(x)=x2 másodfokú függvény alatti területet a [0,2] intervallumon!
Megoldás:
Az f(x)=x2 függvény primitív függvénye: \( F(x)=\frac{x^{3}}{3} \), hiszen \( \left( \frac{x^{3}}{3} \right)^{‘}=x^{2} \).
Így az f(x)=x2 függvény integrálja [0,2] intervallumon:
\[ \int_{0}^{2}{x^{2}dx }=\left [F(x) \right ]_{0}^{2}=\left [\frac{x^{3}}{3}\right ]_{0}^{2}=F(2)-F(0)=\frac{2^{3}}{3}-0=\frac{8}{3} \]
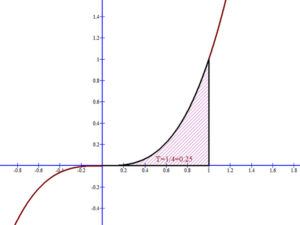
2. Számítsuk ki a Newton-Leibniz képlet segítségével az f(x)=x3 harmadfokú függvény alatti területet a [0,1] intervallumon.
Megoldás:
Az f(x)=x3 függvény primitív függvénye: \( F(x)=\frac{x^{4}}{4} \), hiszen \( \left( \frac{x^{4}}{4} \right)^{‘}=x^{3} \).
Így az f(x)=x3 függvény integrálja: a [0,1] intervallumon:
\[ \int_{0}^{1}{x^{3}dx }=\left [F(x) \right ]_{0}^{1}=\left [\frac{x^{4}}{4}\right ]_{0}^{1}=F(1)-F(0)=\frac{1^{4}}{4}-\frac{0^{4}}{4}=\frac{1}{4}=0.25 \]
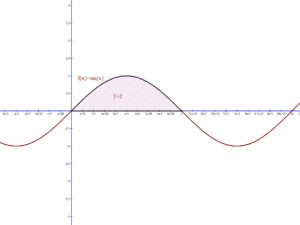
3. Számítsuk ki a Newton-Leibniz képlet segítségével az f(x)=sin(x) trigonometrikus függvény és az „x” tengely által közrefogott síkidom területét a [0,π] majd a [0,2π] intervallumon!
Megoldás:
Az f(x)=sin(x) függvény primitív függvénye: F(x)=-cos(x), hiszen [-cos(x)]’=sin(x).
Így az f(x)=sin(x) függvény integrálja a [0,π] intervallumon:
\[ \int_{0}^{ π }{sin(x)dx }=\left [F(x) \right ]_{0}^{ π }=\left [-cos(x) \right ]_{0}^{ π }=F(π )-(F(0)=(-cos( π )-(-cos(0))=(-(-1)-(-1))=2 \].
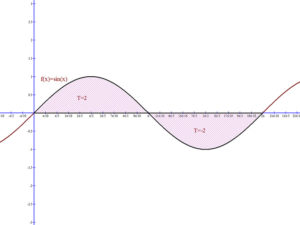Ugyanakkor az f(x)=sin(x) függvény integrálja a [0,2π] intervallumon:
\[ \int_{0}^{2π }{sin(x)dx }=\left [F(x) \right ]_{0}^{2π }=\left [-cos(x) \right ]_{0}^{2π }=F(2π )-(F(0)=(-cos(2π )-(-cos(0))=(-1-(-1)=0 \].
A függvény integrálja nulla, hiszen itt előjeles területekről van szó. A [0,π] intervallumon a görbe alatti terület= 2 területegység, míg a [π,2π] intervallumon a görbe feletti terület= -2 területegység.
Természetesen a két intervallum által meghatározott síkidomok egybevágók, így területük is egyenlő. Tehát egy teljes szinusz hullám által meghatározott terület 4 egységnyi.
Comments are closed, but trackbacks and pingbacks are open.