 1. Példa:
1. Példa:
Egy dobozban 10 darab piros és 8 darab kék golyó van. Csukott szemmel egymás után kihúzunk 5 golyót úgy, hogy minden húzás után visszatesszük a kihúzott golyót és összekeverjük a doboz tartalmát.
Mi a valószínűsége, hogy ötből háromszor piros golyót húztunk?
Megoldás:
Ez visszatevéses mintavétel. A kérdésre a válasz: \( \binom{5}{3}·\left(\frac{10}{18} \right)^3·\left(\frac{8}{18} \right) ^2≈0.34 \).
Ha ezt a kérdést egy picit általánosabban tesszük fel, azaz:
Mi a valószínűsége, hogy ötből „k”-szor piros golyót húztunk? (0≤k≤5)
Ez a valószínűség: \( \binom{5}{k}·\left(\frac{10}{18} \right)^k·\left(\frac{8}{18} \right)^{5-k} \).
2. példa.
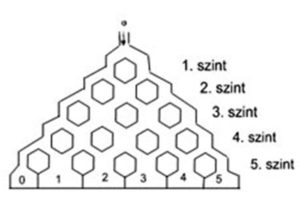 A mellékelt ábrán (Galton deszkán) egy golyó gurul lefelé. Minden akadálynál ugyanakkora (0.5) valószínűséggel megy jobbra vagy balra. Ezért minden út egyformán valószínű. A pályán 5 szinten vannak akadályok (elágazási pontok) és a végén 6 rekesz [0;5] valamelyikébe érkezik meg a golyó.
A mellékelt ábrán (Galton deszkán) egy golyó gurul lefelé. Minden akadálynál ugyanakkora (0.5) valószínűséggel megy jobbra vagy balra. Ezért minden út egyformán valószínű. A pályán 5 szinten vannak akadályok (elágazási pontok) és a végén 6 rekesz [0;5] valamelyikébe érkezik meg a golyó.
Mi a valószínűsége annak, hogy a golyó a k.-dik (0; 1; 2; 3; 4; 5 számú) rekeszbe fog beesni?
Megoldás:
Annak a valószínűsége, hogy a golyó 5 lépés közül k-szor jobbra, (5 – k)-szor balra lép, azaz a k-adik rekeszbe jut: \( \binom{5}{k}·\left(\frac{1}{2}\right)^k·\left(\frac{1}{2} \right)^{5-k} \).
Ez is visszatevéses mintavétel.
Mi a közös a két feladatban?
Olyan eseményekről volt szó mindkettőnél, aminek két lehetséges kimenetele van:
Jobbra – balra, piros – nem piros. Ha az egyik esemény valószínűsége: p, akkor a másiké 1 – p.
Az eredény a Galton deszka esetén: \( \binom{5}{k}·\left(\frac{1}{2}\right)^k·\left(\frac{1}{2} \right)^{5-k} =\binom{5}{k}·\left(\frac{1}{2}\right)^5 \).
Az eredmény a golyós példa esetén: \( \binom{5}{k}·\left(\frac{10}{18} \right)^k·\left(\frac{8}{18} \right)^{5-k} \).
Definíció:
A ξ valószínűségi változót binomiális eloszlásúnak nevezzük, ha ξ lehetséges értékei {0; 1; 2; …n) és eloszlása \( P(ξ=k)=\binom{n}{k}·p^{k}·(1-p)^{n-k} \) , ahol p valószínűség 1-nél nem nagyobb nemnegatív valós szám (p∈ℝ|0≤p≤1) és k lehetséges értékei {0; 1; 2; …n). ( k∈N|0≤k≤n).
A binomiális eloszlás két paramétere: n: ismétlések („visszatevések”) száma, p: valószínűség.
A binomiális eloszlást Bernoulli eloszlásnak is nevezik az un. Bernoulli-kísérlet nyomán.
A visszatevéses mintavétel esetei a binomiális eloszlásra vezetnek.
Feladat:
(2011. májusi emelt szintű érettségi feladat nyomán)
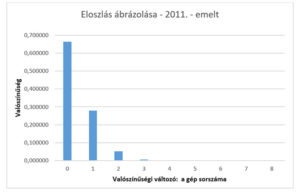
Egy gyártósoron 8 darab gép dolgozik. A gépek mindegyike, egymástól függetlenül 0,05 valószínűséggel túlmelegszik a reggeli bekapcsoláskor. Ha a munkanap kezdetén 3 vagy több gép túlmelegszik, akkor az egész gyártósor leáll. A 8 gép reggeli beindításakor bekövetkező túlmelegedések számát a binomiális eloszlással modellezzük. Adja meg az eloszlás két paraméterét! Számítsa ki az eloszlás várható értékét!
Megoldás:
Ekkor: \( P(ξ=k)=\binom{8}{k}·0,05^{k}·0,95^{k} \) ; ahol k=0; 1; 2;…;8.
Tehát n=8 és p= 0,05.
Készítsünk táblázatot a valószínűségi változó várható értékének és szórásának meghatározásához!
| Valószínűségi változó | Eloszlás, várható érték és szórás | |||||
| Esemény | xi | P(ξ=xi) | xi⋅P(ξ=xi) | ξ-M(ξ) | η=(ξ-M(ξ))2 | η⋅P(ξ=xi) |
| 0 gép romlik el | 0 | 0,663420 | 0,000000 | -0,40 | 0,16 | 0,1061 |
| 1 gép romlik el | 1 | 0,279335 | 0,279335 | 0,60 | 0,36 | 0,1006 |
| 2 gép romlik el | 2 | 0,051456 | 0,102913 | 1,60 | 2,56 | 0,1317 |
| 3 gép romlik el | 3 | 0,005416 | 0,016249 | 2,60 | 6,76 | 0,0366 |
| 4 gép romlik el | 4 | 0,000356 | 0,001425 | 3,60 | 12,96 | 0,0046 |
| 5 gép romlik el | 5 | 0,000015 | 0,000075 | 4,60 | 21,16 | 0,0003 |
| 6 gép romlik el | 6 | 0,000000 | 0,000002 | 5,60 | 31,36 | 0,0000 |
| 7 gép romlik el | 7 | 0,000000 | 0,000000 | 6,60 | 43,56 | 0,0000 |
| 8 gép romlik el | 8 | 0,000000 | 0,000000 | 7,60 | 57,76 | 0,0000 |
| A ξ valószínűségi változó várható értéke: M(ξ)= | 0,400000 | 0,3800 | ||||
| A ξ valószínűségi változó szórása: D(ξ)= | 0,6164 | |||||
Vegyük észre: n⋅p=M(ξ). Ennél a példánál a valószínűségi változó várható értéke: 8⋅0,05=0,4.
Ez az összefüggés általában is igaz.
Tétel:
Ha a ξ „n” és „p” paraméterű valószínűségi változó, akkor várható értéke: M(ξ)=n⋅p.
Azaz a várható érték a két paraméter szorzata.
A következő tétel a szórás kiszámítását teszi egyszerűbbé:
Tétel:
Ha a ξ „n” és „p” paraméterű binomiális eloszlású valószínűségi változó, akkor szórása: \( D(ξ)=\sqrt{n·p·(1-p)} \).
A fenti példa esetén: \( D(ξ)=\sqrt{8·0,05·(1-0,05)}=\sqrt{0,38}≈0,6164 \).
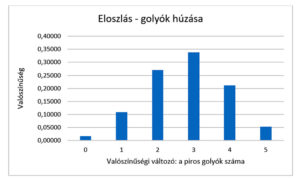
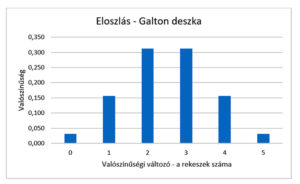
A fenti eloszlások ábrázolása grafikonon:
 |
 |


Comments are closed, but trackbacks and pingbacks are open.