Visszatevéses mintavétel

1. Példa:

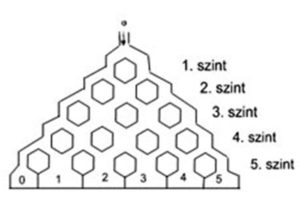
A mellékelt ábrán (Galton deszkán) egy golyó gurul lefelé. Minden akadálynál ugyanakkora (0.5) valószínűséggel megy jobbra vagy balra. Ezért minden út egyformán valószínű. A pályán 5 szinten vannak akadályok (elágazási pontok) és a végén 6 rekesz [0;5] valamelyikébe  érkezik meg a golyó.

Mi a valószínűsége annak,  hogy a golyó a k.-dik (0; 1; 2; 3; 4; 5 számú) rekeszbe fog beesni?

Megoldás:

Ahhoz, hogy golyó a 0. rekeszbe kerüljön, mindig balra kell mennie, ez egy lehetőség. Ennek valószínűsége: ​\( \left(\frac{1}{2} \right) ^5 \)​.  Ez 0.03125, azaz 3.125%-os valószínűség.

Mikor érkezik a golyó a 3. rekeszbe? Ahhoz 3-szor kell jobbra és 2-szer balra kell mennie.
Ezt öt lépés esetén ​\( \binom{5}{3}=10 \)​  féleképpen lehet kiválasztani.
(Kiválasztás úgy, hogy  a sorrend közömbös: ez ismétlés nélküli kombináció. )

Minden döntésnél ​\( \frac{1}{2} \)​valószínűséggel dönt a továbbhaladás irányáról.
Tehát annak valószínűsége, hogy a golyó a 3-as rekeszbe kerül: ​ ​\( \binom{5}{3}·\left( \frac{1}{2} \right)^5 =\frac{10}{32}=0.3125 \)​.​ Ez 31.25%-os valószínűség.

Összefoglalva: Annak a valószínűsége, hogy a golyó a k. rekeszbe kerüljön: ​\( \binom{5}{k}·\left(\frac{1}{2}\right)^5 \)​​.

Ezt másképp is megfogalmazhatjuk:

A golyó minden akadálynál 0.5 valószínűséggel választ a két irány közül, függetlenül attól, hogy előzőleg merre ment. Öt lépése közül a „k” darab balra tartást ​\( \binom{5}{3}=10 \)​ féleképpen lehet kiválasztani.
Ezért annak a valószínűsége, hogy a golyó 5 lépés közül k-szor jobbra, (5 – k)-szor balra lép, azaz a k-adik rekeszbe jut:  ​\( \binom{5}{k}·\left(\frac{1}{2}\right)^k·\left(\frac{1}{2} \right)^{5-k} \)​.

Persze ez a kifejezés a hatványozás azonosságával egyszerűbb alakra hozható:  ​\( \binom{5}{k}·\left(\frac{1}{2}\right)^k·\left(\frac{1}{2} \right)^{5-k} =\binom{5}{k}·\left(\frac{1}{2}\right)^5 \)​.

Ebben az tükröződik, hogy minden döntésnél ugyanakkor (0.5) valószínűséggel választott irányt a golyó.

Mivel a golyó valamelyik rekeszbe biztosan eljut, ezért:

\[ \binom{5}{0}·\left(\frac{1}{2}\right)^5 +\binom{5}{1}·\left(\frac{1}{2}\right)^5 +\binom{5}{2}·\left(\frac{1}{2}\right)^5 \binom{5}{3}·\left(\frac{1}{2}\right)^5 +\binom{5}{4}·\left(\frac{1}{2}\right)^5 +\binom{5}{5}·\left(\frac{1}{2}\right)^5 =1 \]

Mivel kiemeléssel: ​\( \left(\binom{5}{0}+\binom{5}{1}+\binom{5}{2}+ \binom{5}{3}+\binom{5}{4}+\binom{5}{5} \right)·\left( \frac{1}{2}\right)^5=1 \)​.

A binomiális tétel szerint: ​\( \binom{5}{0}+\binom{5}{1}+\binom{5}{2}+ \binom{5}{3}+\binom{5}{4}+\binom{5}{5} =2^5 \)​ . Ezért ​\( 2^5·\left( \frac{1}{2}\right) ^5=1 \)​.
A biztos esemény valószínűsége: 1.

2. Példa:

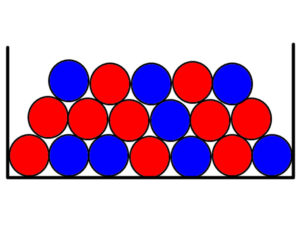
Egy dobozban 10 darab piros és 8 darab kék golyó van. Csukott szemmel egymás után kihúzunk 5 golyót úgy, hogy minden húzás után visszatesszük a kihúzott golyót és összekeverjük a doboz tartalmát.
Mi a valószínűsége, hogy ötből háromszor piros golyót  húztunk?

Megoldás:

Ha háromszor pirosat húztunk, akkor kétszer kéket kellett húzni, hiszen csak kétféle golyó volt a mintában.

Mivel a kihúzott golyót visszatesszük, ezért minden húzásnál a piros golyó húzásának a valószínűsége: ​\( \frac{10}{18} \)​, a kék golyó húzásának a valószínűsége mind az 5 húzáskor ​\( \frac{8}{18} \)​.

A piros golyók húzásának a helye (sorrendje) ​\( \binom{5}{3}=10 \)​ féleképpen lehetséges.

Így a keresett valószínűség: ​\( \binom{5}{3}·\left(\frac{10}{18} \right)^3·\left(\frac{8}{18} \right) ^2≈0.34 \)​.

Ha ezt a példát egy picit általánosabban tesszük fel, azaz:

Mi a valószínűsége, hogy „k” darab piros golyót húztunk?

Az előző gondolatmenetet követve ez a valószínűség: ​\( \binom{5}{k}·\left(\frac{10}{18} \right)^k·\left(\frac{8}{18} \right)^{5-k} \)​.

Még általánosabban:

„N” darab golyó között kétféle színű (maradjunk a piros és kék színeknél) golyó van. Legyen „M” darab a piros. Így N-M darab a kék golyók száma. Az „N” darab golyóból kihúzunk „n” darab golyót. (n<N). A kihúzott golyót minden esetben visszatesszük.

Ebben az esetben mi a valószínűsége, hogy „k” darab piros golyót húztunk?

Minden húzásnál a ​\( \frac{M}{N} \)​ piros golyó húzásának a valószínűsége: és persze ​\( \frac{N-M}{N} \)​ valószínűséggel húzunk kék golyót.

A piros golyót helye (sorrendje) ​\( \binom{n}{k} \)​ féleképpen lehetséges.

Így a keresett valószínűség:  ​\( \binom{n}{k}·\left(\frac{M}{N} \right)^k·\left(\frac{N-M}{N} \right)^{n-k} \)​.

Legyen „p” valószínűsége egy adott tulajdonságú elem választásának. A fenti példában  ​p=\( \frac{M}{N} \)​ . Ekkor az ezzel a tulajdonsággal nem rendelkező elemek választásának a valószínűsége 1-p.

Definíció:

A visszatevéses mintavételnél n elem közül p valószínűséggel választunk valamilyen tulajdonsággal rendelkezőt oly módon, hogy a kivett elemet az újabb húzás előtt visszatesszük.

A visszatevéses mintavételnél „k” darab kiválasztása estén a a valószínűség: ​

\( \binom{n}{k}·p^k·(1-p)^{n-k} \)​.

A visszatevéses mintavétel esetei a binomiális eloszlásra vezetnek.