Vektorok vektoriális szorzata

Vektorok skaláris szorzatához hasonlóan szintén a fizikából eredeztetjük vektorok vektoriális szorzatát. Amikor két vektor szorzata nem egy szám, hanem egy harmadik vektor.

A legegyszerűbb értelmezés szerint a forgatónyomaték a forgató hatást létrehozó erőnek és az erőkarnak a vektoriális szorzata: ​​\( \vec{M}=\vec{F}×\vec{r} \)​.

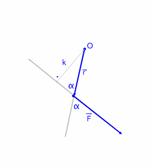
A mellékelt ábrán az O pont a forgáspont, ​\( \vec{F} \)​ az erő, \( \vec{r} \)​  a forgáspontból az erő támadáspontjához mutató helyvektor. Az erő és a helyvektor által bezárt szög pedig α.

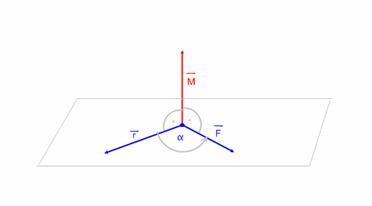
Az ​\( \vec{M} \)​ forgatónyomatékhoz a fizika úgy rendel vektort, hogy az ​\( \vec{M} \) merőleges az ​\( \vec{F} \)​ és az ​\( \vec{r} \)​ által kifeszített síkra, továbbá az ​\( \vec{r} \)​, ​\( \vec{F} \)​ és az ​\( \vec{M} \)​ebben a sorrendben jobbrendszert alkot.

Definíció:

Két, egymással „α” szöget bezáró (​\( \vec{a} \) és ​\( \vec{b} \)​) vektor vektoriális (külső) szorzatának nevezzük azt a (​\( \vec{c} \)​) vektort, amelynek abszolút értéke a két adott vektor abszolút értékének és az általuk bezárt szög szinuszának a szorzata, iránya merőleges az adott vektorokra, úgy, hogy a vektoriális szorzat vektorával (eredmény vektor) szembenézve az első vektor 180°-nál kisebb pozitív irányú forgatással legyen átvihető a másodikként megadott vektorral egyező irányba.

A művelet jelölése: ​\( \vec{a}×\vec{b} \)​ (olvasd: a kereszt b) .

Művelet formulával: ​\( \vec{a}×\vec{b}=\vec{c} \)​, ahol |​\( \vec{c} \)​| = |​\( \vec{a} \)​|⋅|​\( \vec{b} \)​|⋅sinα.

Itt ​\( \vec{c} \)​⊥ ​\( \vec{a} \)​, \( \vec{c} \) ⊥ \( \vec{b} \) , valamint az ​\( \vec{a} \)​,  ​\( \vec{b} \)  és \( \vec{a}×\vec{b}=\vec{c} \) ebben a sorrendben jobbrendszert alkot.

Az |​\( \vec{a} \)​|⋅|​\( \vec{b} \)​|⋅sinα szorzat értéke az ​\( \vec{a} \)​ és ​\( \vec{b} \) vektorok által kifeszített paralelogramma területével egyenlő.

Ezért szokták az ​\( \vec{a}×\vec{b} \)​ vektoriális szorzatot az ​\( \vec{a} \) és ​\( \vec{b} \) vektorok által kifeszített paralelogramma területvektorának is nevezni.

Vektoriális szorzás tulajdonságai.

1) A definíció közvetlen következménye, hogy ha az ​\( \vec{a} \)​ és ​\( \vec{b} \)​ vektorok közül az egyik vektor nullvektor, akkor az ​\( \vec{a}×\vec{b} \)​ vektor is nullvektor lesz.

2) Ha az \( \vec{a} \) és \( \vec{b} \) vektorok párhuzamosak, akkor a közbezárt szögük szinusza nulla, ebből következik, hogy az ilyen vektorok vektoriális szorzata nulla.

Tétel:

Két vektor vektoriális szorzata akkor és csak akkor nulla, ha a két vektor párhuzamos egymással.

3) A vektoriális szorzás antikommutatív. Azaz: ​\( \vec{a}×\vec{b}=-(\vec{b}×\vec{a}) \)​ .

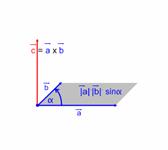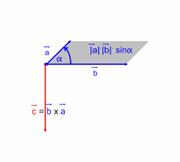4) A vektoriális szorzás nem asszociatív.
Tekintsük az​\( \vec{i} \)​; \( \vec{j} \)​ és \( \vec{k} \)​ bázisvektorokat, ahol ​\( \vec{k}=\vec{i}×\vec{j} \)​.
Egyrészt:  ​\( (\vec{i}×\vec{i})×\vec{j}=\vec{0}×\vec{j}=\vec{0} \)​. Az eredmény tehát a nullvektor.
Másrészt:  ​\( \vec{i}×(\vec{i}×\vec{j})=\vec{i}×\vec{k}=-\vec{j} \).

5) A vektoriális szorzat disztributív (tagolható):  ​\( \vec{a}×(\vec{b}+\vec{c})=\vec{a}×\vec{b}+\vec{a}×\vec{c} \)​ .