A vektort mint irányított szakaszt definiáljuk. Az eltolást vektorral adjuk meg.
Vektorok összeadása:
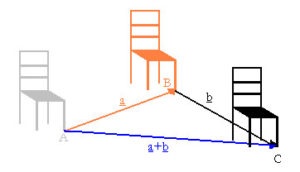 Két vektor összegét mint két eltolás egymásutánját értelmezzük.
Két vektor összegét mint két eltolás egymásutánját értelmezzük.
Két vektor összeadásakor az egyik vektor végpontjába felmérjük a másik vektort. Az összegvektor az első kezdőpontjából a másik vektor végpontjába mutat.
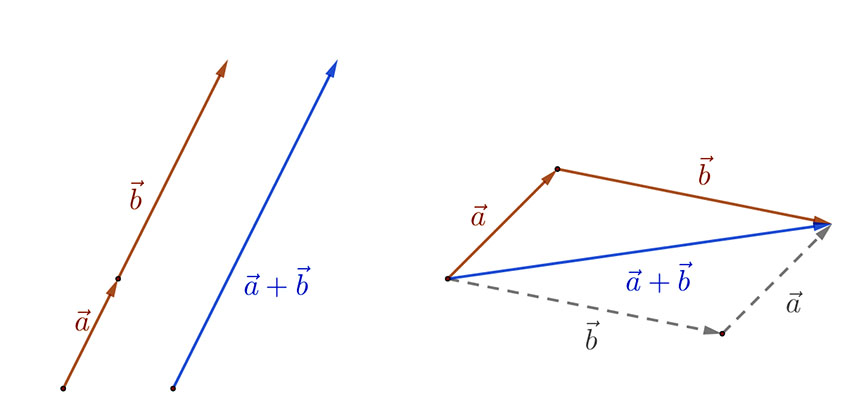 Szöget bezáró vektorok esetén a két vektort közös kezdőpontba is mérhetjük. Ekkor végpontjaikból párhuzamosokat húzva, paralelogrammát kapunk. Ennek a paralelogrammának a vektorok közös kezdőpontjából kiinduló átlója lesz az összegvektor.
Szöget bezáró vektorok esetén a két vektort közös kezdőpontba is mérhetjük. Ekkor végpontjaikból párhuzamosokat húzva, paralelogrammát kapunk. Ennek a paralelogrammának a vektorok közös kezdőpontjából kiinduló átlója lesz az összegvektor.
Három vagy több vektor összeadásakor a vektorokat egymáshoz csatlakoztatva vesszük fel. Az összegvektor az első vektor kezdőpontjából az utolsó vektor végpontjába mutat.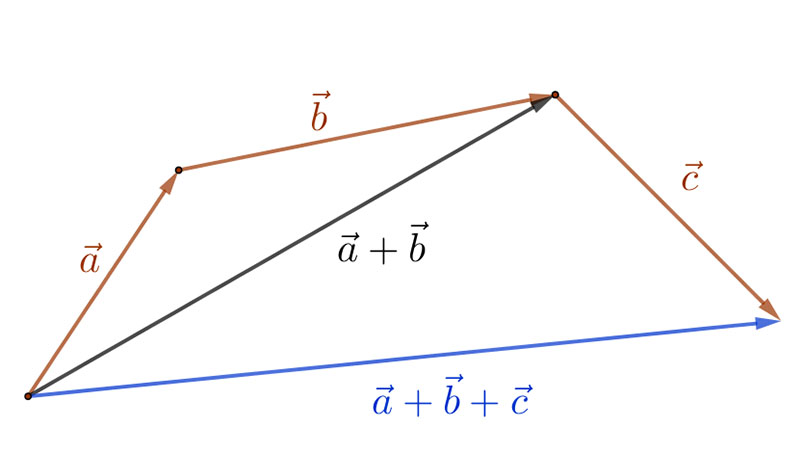
Vektorösszeadás tulajdonságai:
1. A vektorösszeadás kommutatív, azaz az összeadandó vektorok felcserélhetők: \( \vec{a} \)+\( \vec{b} \)=\( \vec{b} \)+\( \vec{a} \).
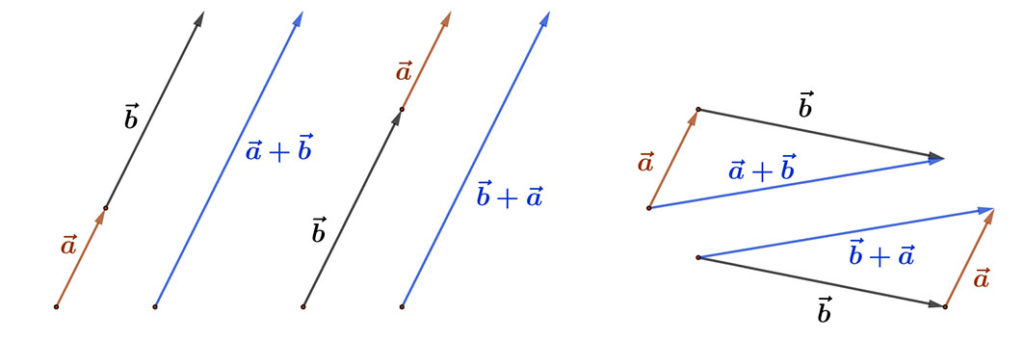
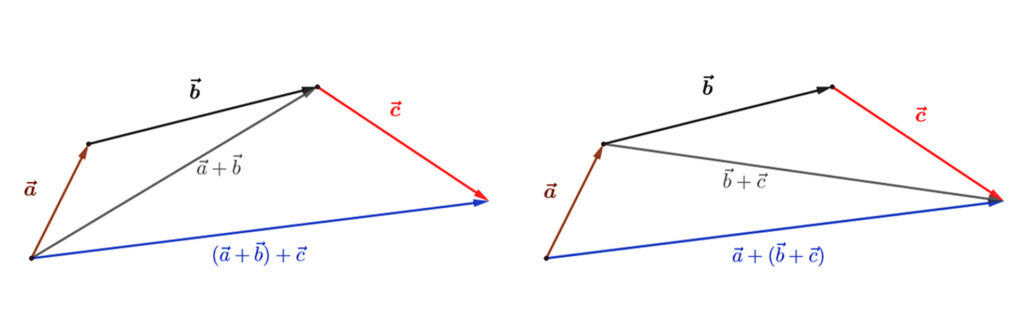
2. Vektorok összeadása asszociatív, azaz több vektor esetén az összeadandó vektorokat tetszőlegesen csoportosíthatjuk: ( \( \vec{a} \)+\( \vec{b} \))+\( \vec{c} \)=\( \vec{a} \)+(\( \vec{b} \)+\( \vec{c} \)).
Vektorok különbsége:
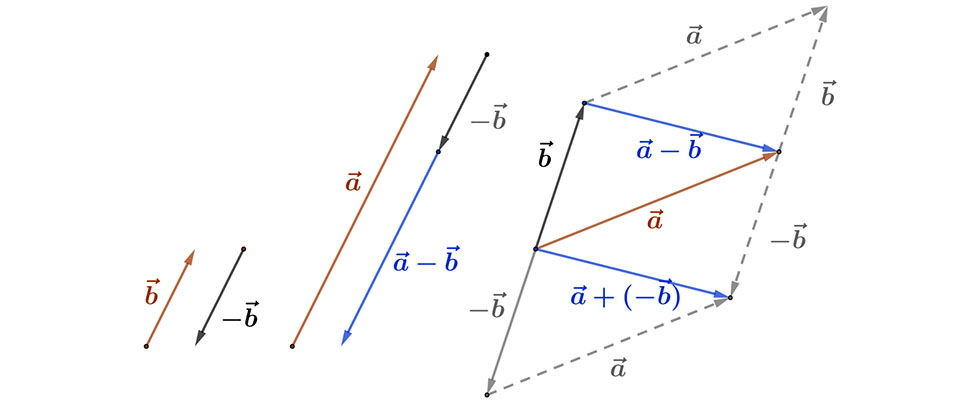
Két vektor különbségén az ellentett vektor hozzáadását értjük.
Jelöléssel: \( \vec{a}-\vec{b}=\vec{a}+(-\vec{b}) \).
Két vektor különbségének megszerkesztésekor a két vektort közös kezdőpontból mérjük fel. A különbségvektor a kivonandó vektor végpontjából a kisebbítendő vektor végpontjába mutat.
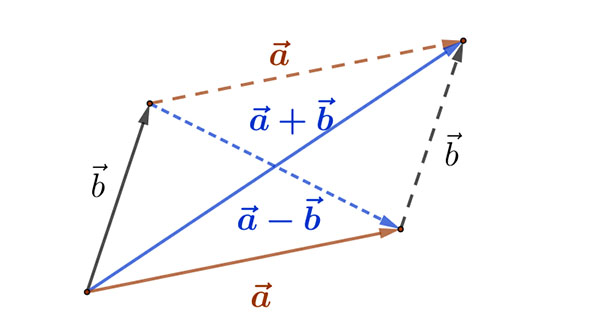
Két vektor összegének és különbségének a paralelogramma szabály szerinti megszerkesztését mutatja a mellékelt ábra:


Comments are closed, but trackbacks and pingbacks are open.