Legyen adott egy véges A halmaz. Jelölje n az A halmaz elemeinek a számát: n=|A|.
Például: A={a, b, c, d}. Ekkor |A|=n=4.
Hány részhalmaza van ennek az A halmaznak?
Azt tudjuk, hogy az üres halmaz minden halmaznak részhalmaza, és minden halmaz részhalmaza önmagának.
Szedjük táblázatba az A halmaz lehetséges részhalmazait:
| Elemszám | Részhalmazok | Részhalmazok száma |
| Nulla elemű halmaz: | Ø ={}, az üres halmaz. | 1 darab |
| Egyelemű részhalmazok: | {a}, {b}, {c}, {d} | 4 darab |
| Kételemű részhalmazok: | {a,b}, {a,c}, {a,d}, {b,c}, {b,d}, {c,d} | 6 darab |
| Háromelemű részhalmazok: | {a,b,c}, {a,b,d},{a,c,d}, {b,c,d} | 4 darab |
| Négyelemű (nem valódi) részhalmaz: | {a,b,c,d}=A, azaz önmaga | 1 darab |
| Összesen: | 16 darab |
Most általánosítsunk.
Egy n elemű halmaznak annyi egyelemű részhalmaza van, ahányféleképpen ki lehet választani az n elemből 1-t. Ezt \( \binom{n}{1}=n \) féleképpen lehet.
Ha a k elemű (k≤n) részhalmazokat nézzük, ebből annyi van, ahányféleképpen ki lehet választani az n elemből k darabot, azaz \( \binom{n}{k} \) féleképpen.
Célszerű most is egy hasonló táblázatot készíteni:
| Részhalmaz elemeinek száma | Részhalmazok száma. |
| Nullaelemű halmaz Ø={}, az üres halmaz: | \( \binom{n}{0}=1 \) |
| Egyelemű részhalmaz: | \( \binom{n}{1} =n \) |
| Kételemű részhalmaz: | \( \binom{n}{2}=\frac{n·\left(n-1 \right) }{2} \) |
| …. | |
| k elemű részhalmaz: | \( \binom{n}{k} \) |
| … | |
| n elemű (nem valódi) részhalmaz: | \( \binom{n}{n} =1 \) |
Részhalmazok száma ezek összege:
\[ \sum_{k=0}^{n}{\binom{n}{k} }= \binom{n}{0} + \binom{n}{1} + \binom{n}{2} +…+\binom{n}{k})+…+ \binom{n}{n} \]
A kérdés úgy is feltehető, hogy mennyit ér a binomiális együtthatók összege?
Induljunk ki a binomiális tételből:
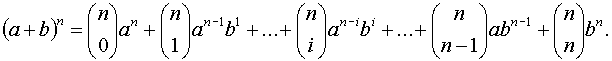
Ha a binomiális tételben szereplő a és b változók helyére 1-t írunk:
\[ \left(1+1 \right) ^{n}= 2^{n}=\binom{n}{0} + \binom{n}{1} + \binom{n}{2} +…+\binom{n}{k})+…+ \binom{n}{n} \]
Ez tehát azt jelenti, hogy egy n elemű véges halmaznak 2n számú részhalmaza van.
Feladat:
Hány elemű az a halmaz, amelynek legalább ezerrel több részhalmaza van, mint ahány eleme?
(Összefoglaló feladatgyűjtemény 164. feladat.)
Megoldás:
Jelölje most x a keresett halmaz elemeinek a számát. Ennek a halmaznak a fenti tétel értelmében 2x számú részhalmaza van.
A feladat kérdése a következő egyenlőtlenségben írható fel:
Részhalmazok száma 2x elemek száma+1000.
Azaz: 2x ³ x+1000.
Ezt az egyenlőtlenséget hagyományos középiskolai algebrai eszközökkel nem tudjuk megoldani. Ha azonban végigfutunk 2 egész kitevőjű hatványain, „hamar” megtaláljuk azt a kitevőt, amelyre a fenti egyenlőtlenség teljesül:
21=2; 22=4; 23=8; 24=16; 25=32; 26=64; 27=128; 28=256; 29=512; 210=1024.
210=1024 > 10+1000=1014.
Eredmény:
x≥10, mert minden olyan halmaz, amelynek legalább 10 eleme van, annak legalább 1000-el több részhalmaza van, mint amennyi az elemeinek száma.


Comments are closed, but trackbacks and pingbacks are open.