1. Függvény konstans-szorosának deriváltja
Tétel:
Ha f (x) függvény differenciálható egy x0 pontban akkor a c f(x) függvény is differenciálható ebben az x0 pontban és (cf(x0))’ =c f’(x0). Röviden: (cf(x))’ =c f’(x).
Másképp: Egy függvény konstans-szorosának deriváltja a függvény deriváltjának konstans-szorosa.
2. Két függvény összegének és különbségének deriváltja
Feladat:
Határozzuk meg a következő függvények differenciálhányadosát az x0 = 3 pontban és írjuk fel a derivált függvényeiket! f(x)=x2 és g(x) = -4x+3
Megoldás:
\[ f'(x_{0}=3)=lim_{ x \to 3}\frac{x^2-3^2}{x-3}=\lim_{ x \to 3 }\frac{(x-3)(x+3)}{x-3}=\lim_{ x \to 3 }(x+3)=6. \]
Így f’(x=3)=6.
\[ g'(x_{0}=3)=lim_{ x \to3 }\frac{(-4x+3)-(-4·3+3)}{x-3}=\lim_{ x \to 3}\frac{-4x+12}{x-3}=\lim_{ x \to 3 }\frac{-4(x-3)}{x-3}=-4. \]
Így g’(x=3)=-4.
Képezzük most a fenti két függvény összegét: c(x)=f(x)+g(x), azaz c(x)=x2+ 4x+3.
\[ c'(x_{0}=3)=\lim_{ x \to 3}\frac{(x^2-4x+3)-(3^2-4·3+3)}{x-3}=\lim_{ x \to 3}\frac{x^2-4x+3}{x-3}=lim_{ x \to 3}\frac{(x-3)(x-1)}{x-3}=\lim_{ x \to 3}(x-1)=2 .\]
Így c’(x=3)=6+(-4)=2.
Tétel:
Ha f (x) és g(x) függvény differenciálható egy x0 pontban akkor f(x)+g(x) is differenciálható ebben az x0 pontban és (f(x0)+g(x0))’ = f’(x0) +g’(x0). Röviden: (f(x)+g(x))’ = f’(x) +g’(x).
Másképp: Az összegfüggvény deriváltja a tagok deriváltjainak összege.
Tétel következménye:
Legyen adott a p(x)=an⋅xn+ an-1⋅xn-1+an-2⋅xn-2+…+a2⋅x2 +a1⋅x1 +a0 polinom függvény.
Ekkor deriváltja: p'(x)=an⋅xn-1+ an-1⋅xn-2+an-2⋅xn-3+…+a2⋅x1 +a1.
Példa:
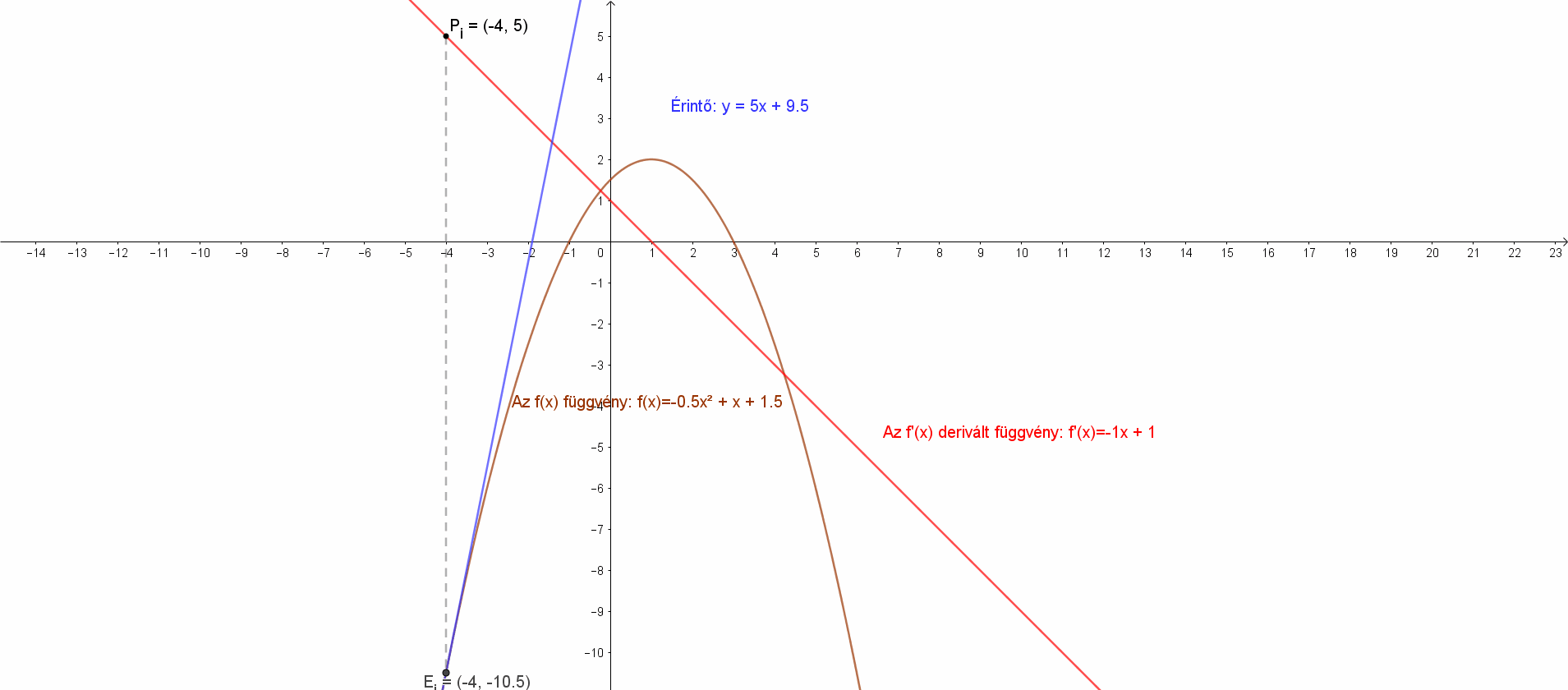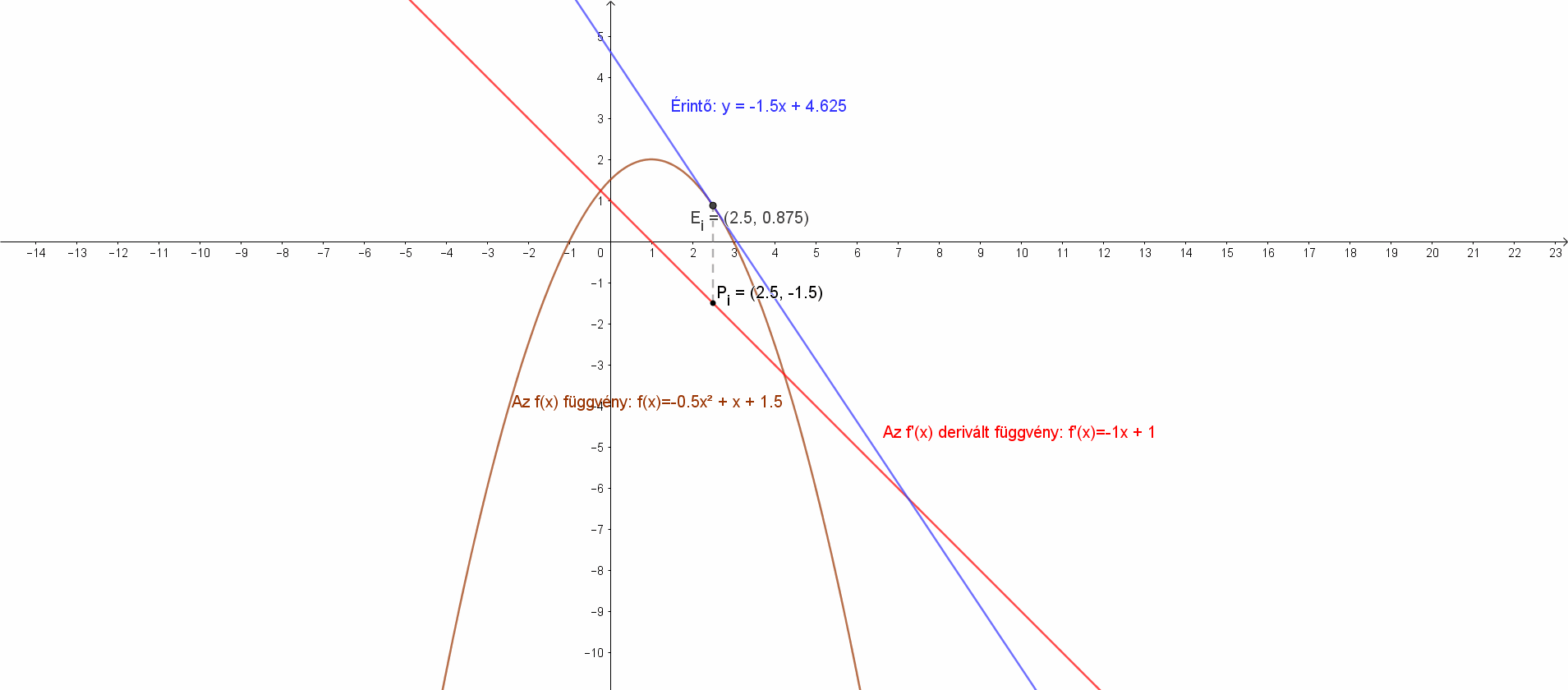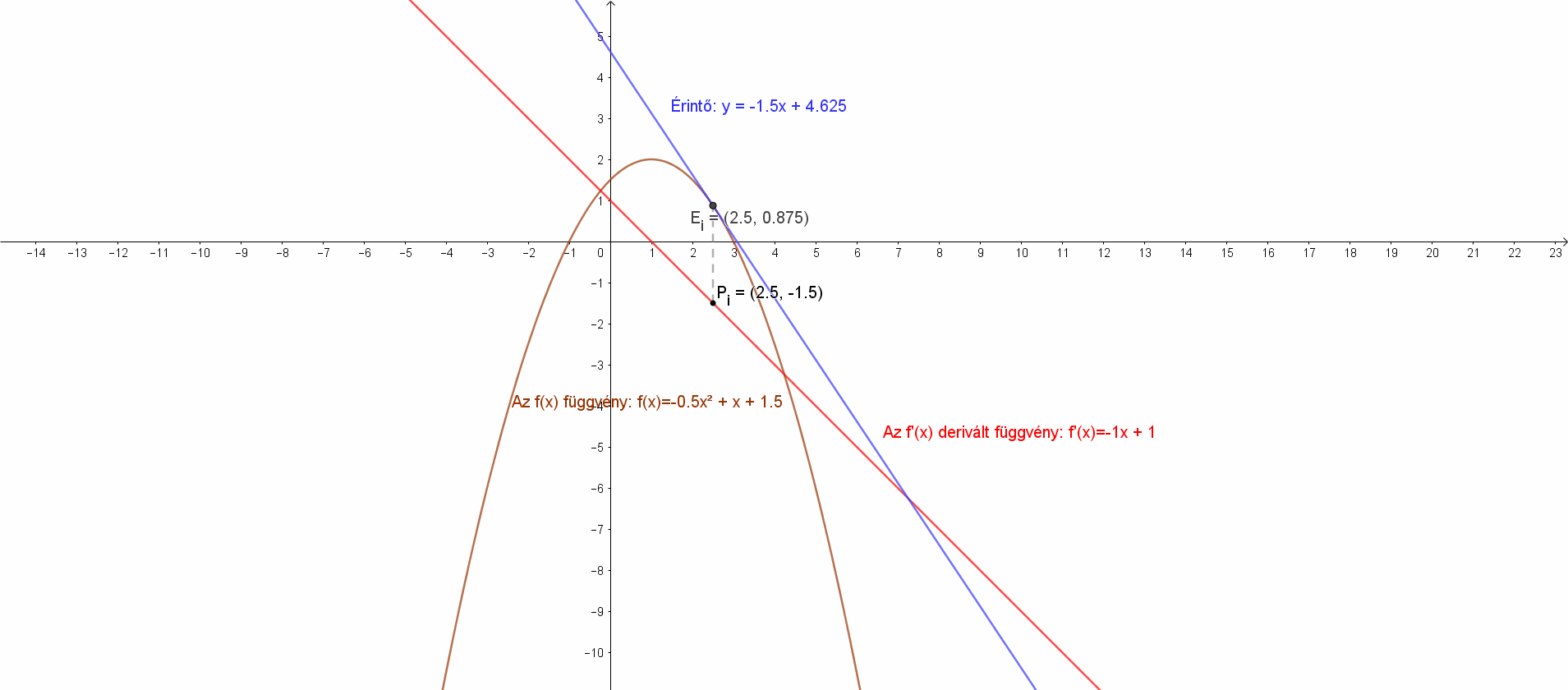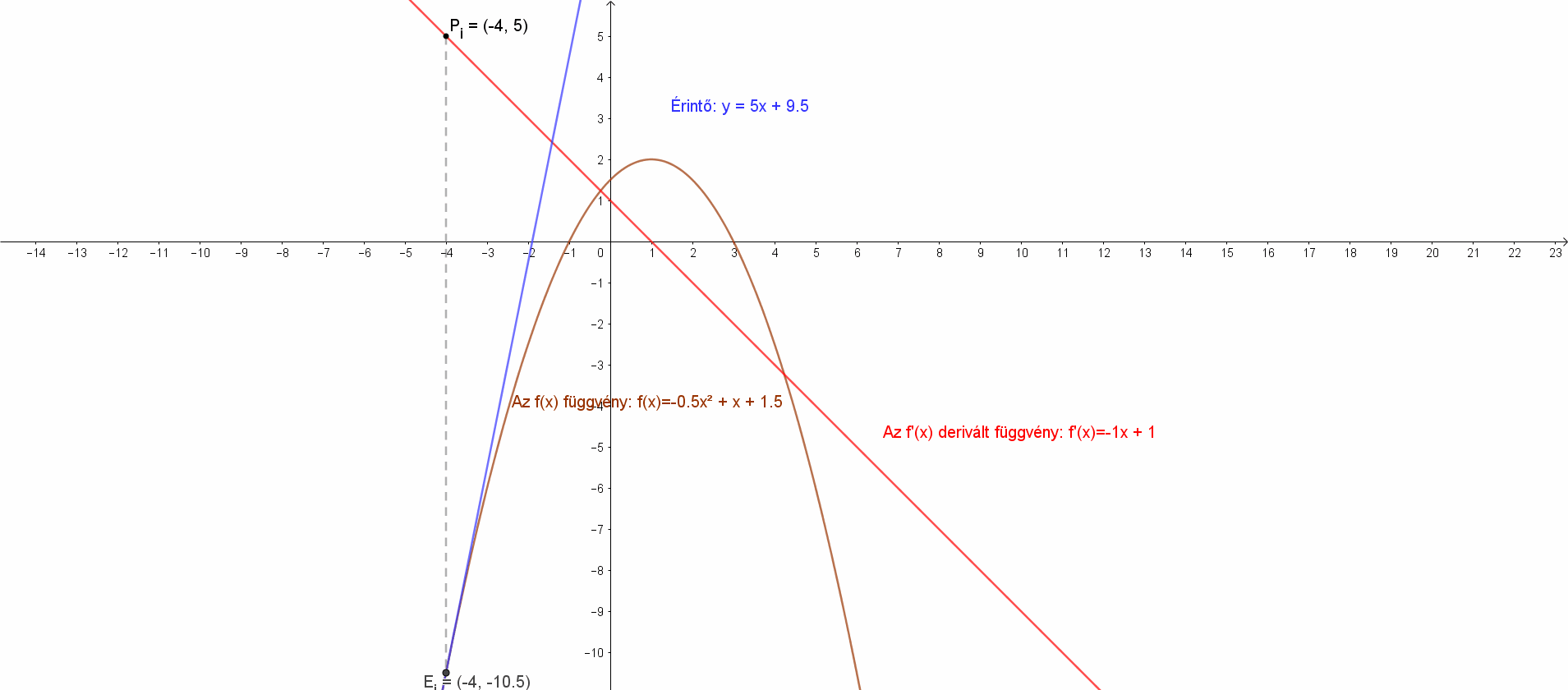
Deriváljuk a következő függvényt: f(x)=-0.5x2+x+1.5! Határozzuk a függvény érintőinek meredekségét a következő pontokban: x0=-1; x0=-0.5; x0=0; x0=0.5; x0=1; x0=2! Írjuk fel az érintők egyenleteit ezekben a pontokban!
Megoldás:
A derivált függvény a fentiek értelmében: f'(x)=(-0.5x2+x+1.5)’=-1⋅x+1.
Az derivált függvény értékei az adott pontban az érintő meredeksége és az érintő egyenlete.
Az f'(-1)=2, ezért m=2, az érintő: y=2x+2.
Az f'(-0.5)=1.5, ezért m=1.5, az érintő: y=1.5⋅x+1.625.
Az f'(0)=1, ezért m=1, az érintő: y=1⋅x+1.5.
Az f'(0.5)=1, ezért m=0.5, az érintő: y=0.5⋅x+1.625.
Az f'(1)=1, ezért m=0, az érintő: y=2.
Az f'(1.5)=1, ezért m=-0.5, az érintő: y=-0.5⋅x+2.625.
Az f'(2)=-1, ezért m=-1, az érintő: y=-1⋅x+3.5.
3. Szorzat függvény deriválása
Feladat:
Legyen a(x)=x2-1 és \( b(x)=\sqrt{x} \). Írjuk fel a két függvény derivált függvényét! Mivel egyenlő a két függvény szorzatának derivált függvénye?
Megoldás:
Képezzük a két függvény szorzatát: c(x)=a(x)⋅b(x)=\( (x^2-1)\sqrt{x} \).
A hatványfüggvények deriválási szabálya szerint: a'(x)=2⋅x és \( b'(x)=\frac{1}{2⋅\sqrt{x}} \).
Mivel lehet egyenlő a c'(x)=[a(x)⋅b(x)]’?
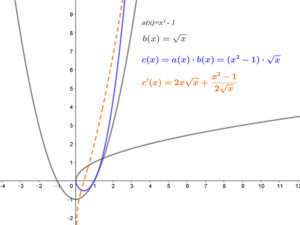 Hívjuk segítségül a számítógépes függvény rajzolást!
Hívjuk segítségül a számítógépes függvény rajzolást!
A számítógépes grafikon szerint az eredmény: \( c'(x)=2x·\sqrt{x}+(x^2-1)\frac{1}{2·\sqrt{x}} \).
Innen már sejthető a következő tétel:
Ha f (x) és g(x) függvény differenciálható egy x0 pontban akkor f(x)g(x) is differenciálható ebben az x0 pontban és (f(x0)g(x0))’ = f’(x0)g (x0)+ f(x0)g’(x0).
Röviden: (f(x)g(x))’ = f’(x)g(x) +f(x)g’(x).
Megjegyzés: A fenti feladat megkerülhető, ha a c(x) függvényt polinom függvényként kezeljük.
4. Hányados függvény deriválása
Tétel:
Ha f (x) és g(x) függvény differenciálható egy x0 pontban akkor a \( c(x)=\frac{f(x)}{g(x)} \) függvény is differenciálható ebben az x0 pontban és \( c'(x_0)=\left [ \frac{f(x_0)}{g(x_0)}\right ] ‘=\frac{f'(x_0)·g(x_0)-f(x_0)·g'(x_0)}{g^2(x_0)} \), feltételezve, hogy g(x0)≠0.
Röviden: \( c'(x)=\left [ \frac{f(x)}{g(x)}\right ] ‘=\frac{f'(x)·g(x)-f(x)·g'(x)}{g^2(x)} \), g(x)≠0.
Feladat:
Mi a deriváltja a \( c(x)=\frac{x+1}{x^2+1} \) függvénynek?
Megoldás:
A fenti összefüggés alkalmazásával:
\[ c'(x)=\frac{1·(x^2+1)-(x+1)·2x}{(x^2+1)^2}=\frac{(-x^2-2x+1)}{(x^4+2x^2+1)} \].
Grafikon: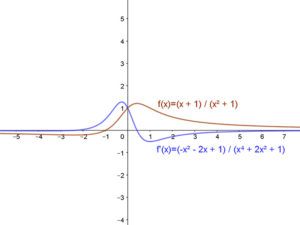
5. Az összetett függvények deriválási szabálya
Ha a g(x) függvény deriválható az x0 pontban és az „f” függvény deriválható a (g(x0)) helyen, akkor az f(g(x0)) összetett függvény is deriválható az x0 helyen és a deriváltja: \( \left [f(g(x_0)) \right ]’=f'(g(x_0))·g'(x_0) \).
Ha x0 az értelmezési tartomány tetszőleges helye, akkor az összetett függvény deriváltja: \( \left [f(g(x)) \right ]’=f'(g(x))·g'(x) \).
Feladat:
Deriváljuk az \( f(x)=\sqrt{x^2-2x-3} \) függvényt!
Megoldás:
Ennek a függvénynek az értelmezési tartománya a √ miatt: x∈ℝ|x≤-1 vagy x≥3.
A fenti összetett függvénynél a külső függvény a √ függvény, a belső g(x) függvény pedig másodfokú függvény.
Alkalmazva az összetett függvényre vonatkozó összefüggést, kapjuk: \( f'(x)=\frac{1}{2\sqrt{x^2-2x-3}}·(2x-2) \).
A derivált függvény értelmezési tartománya az eredetihez képest szűkül, mivel a nevező nem lehet nulla, tehát x∈ℝ|x<-1 vagy x>3.
6. Inverz függvény deriváltja
Ha az f(x) függvénynek létezik inverz függvénye f-1(x) az ]a;b[ nyílt intervallumon és f(x) differenciálható az x0∈]a;b[ pontban, akkor az f-1(x) függvény differenciálható ebben a pontban és \( \left [ f^{-1}(x) \right ]’=\frac{1}{\left [f(f^{-1}(x)\right ]’ } \).
Példa
Legyen az f(x)=x2, x∈[0;+∞[. Ennek a függvénynek van inverze a [0+∞[ intervallumon és f-1 (x)=√x. Határozzuk meg az f-1(x) függvény deriváltját a a fenti összefüggés alkalmazásával.
Ha ebben az estben alkalmazzuk az inverz függvényre vonatkozó szabályt, akkor \( \left [ f^{-1}(x) \right ]’=\frac{1}{\left [ (\sqrt{x})^2 \right ]’ }=\frac{1}{2\sqrt{x}} \).
Összhangban avval, hogy \( g'(x)=(\sqrt{x})’=\frac{1}{2\sqrt{x}} \).
Hiszen (z2)’=2⋅z, ahol \( z=\sqrt{x} \).
∈ℕℤℚℝ


Comments are closed, but trackbacks and pingbacks are open.