Adott meredekségű egyenes egyenlete

Adott az egyenes egy pontja: P₀(x₀;y₀) és adott az egyenes irányvektora: \( \vec{v}(v_1;v_2) \)​ .

Az egyenes irányvektoros egyenletéből indulunk ki, amely a következő: v₂x-v₁y=v₂x₀-v₁y₀ az alábbi animációs ábra  jelölései szerint.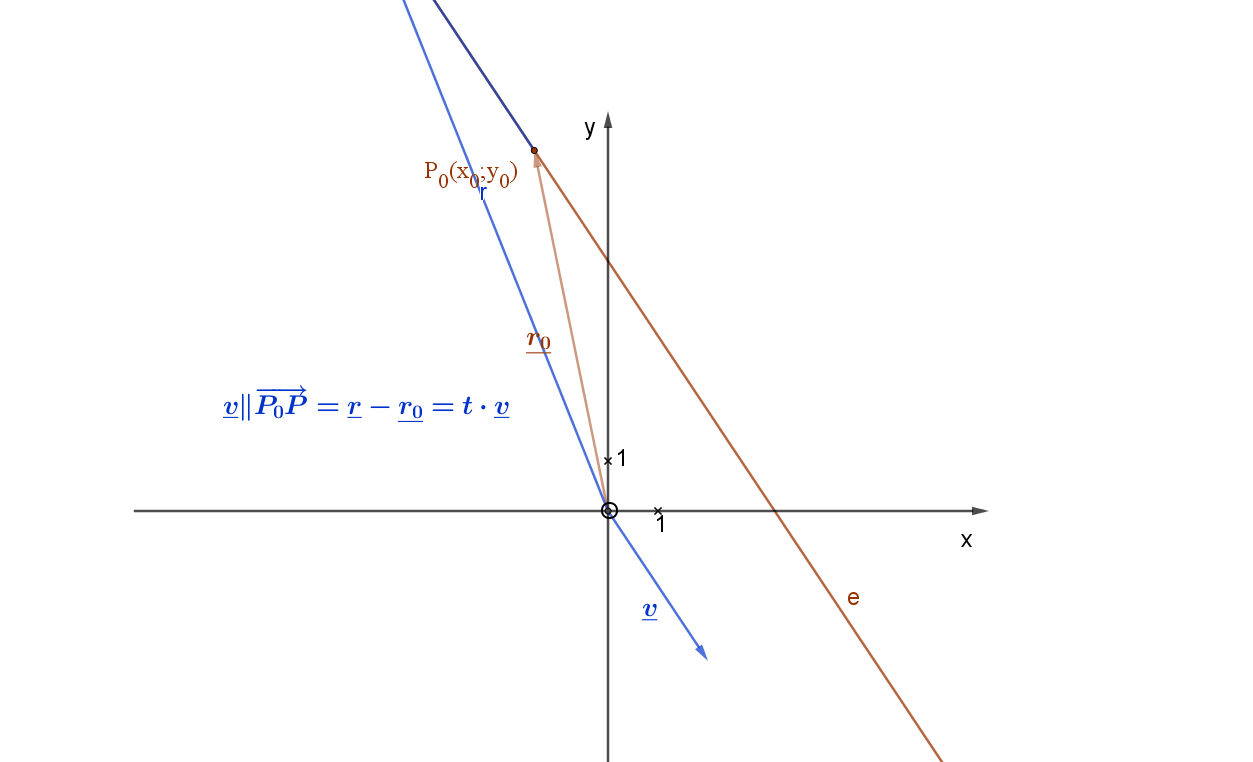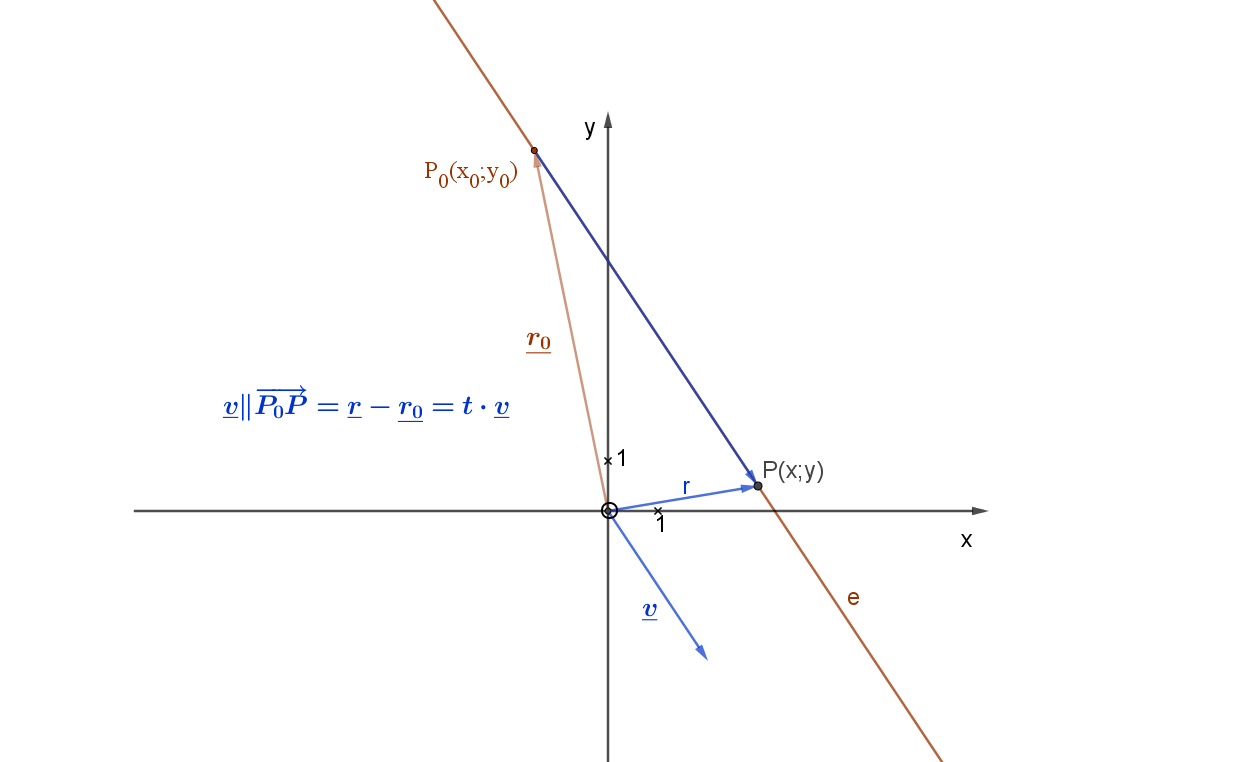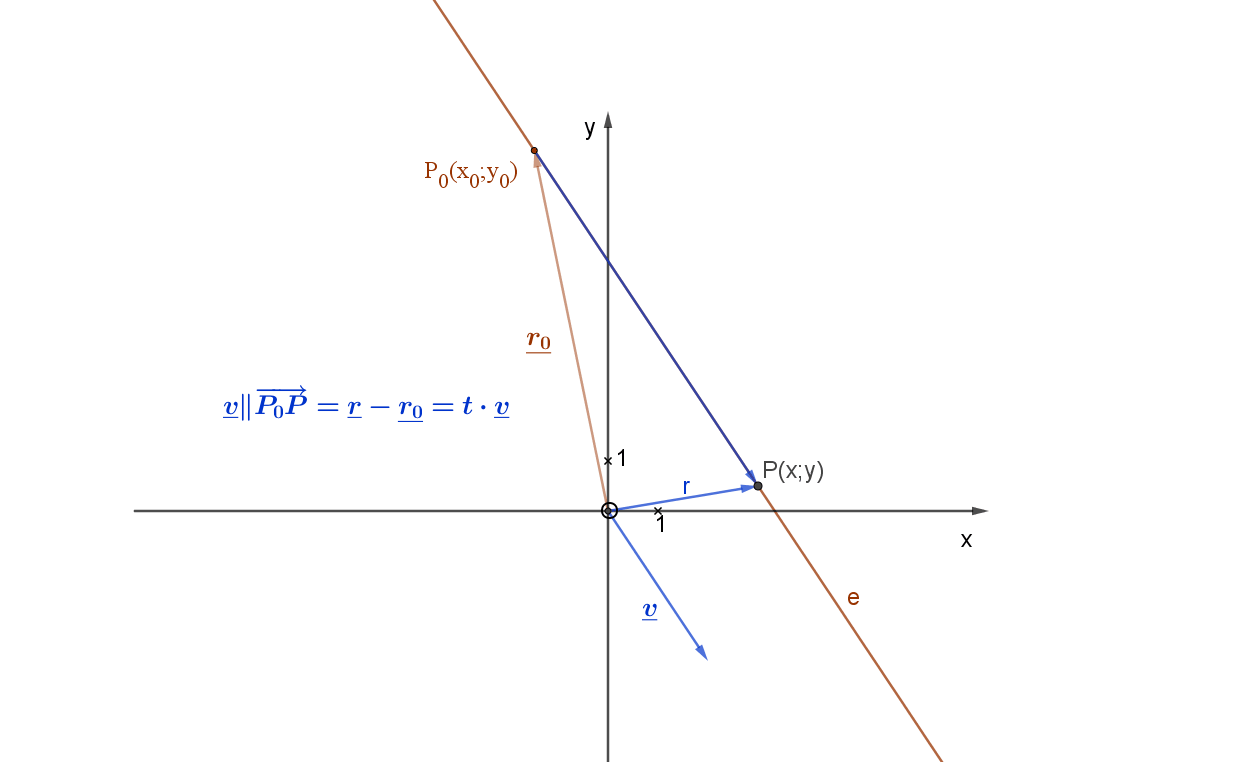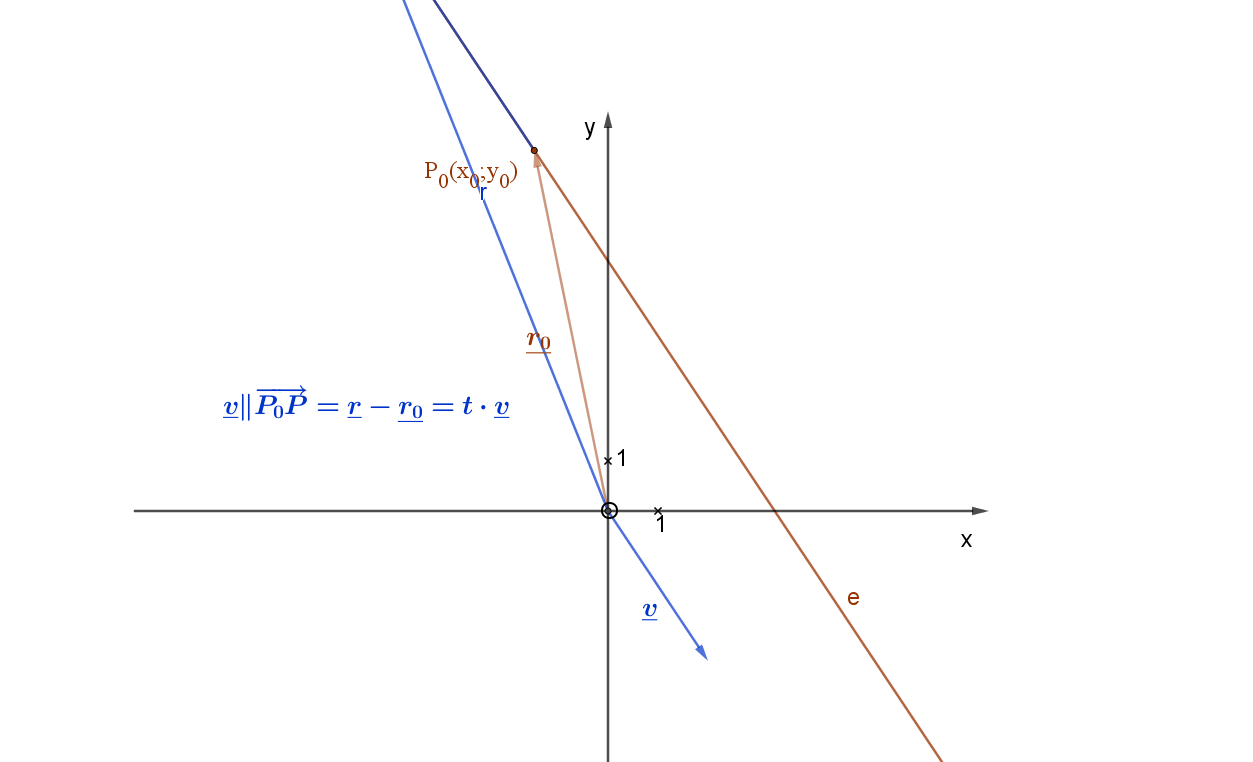
Egyenes iránytangense csak akkor létezik, ha az egyenes nem párhuzamos az y tengellyel. Ebben az esetben az egyenes irányvektorának első koordinátája biztosan nem nulla, azaz v₁≠0.

Ekkor az egyenes iránytangensét az irányvektor második és első koordinátájának hányadosaként értelmezzük, azaz m=v₂/v₁ (v₁≠0).

Mivel az egyenes irányvektora tetszőleges, az egyenessel párhuzamos vektor, az irányvektor első koordinátáját tekinthetjük 1-nek (v₁=1), azaz  ​\( \vec{v}(v_{1},v_{2}) \)​.
Ekkor m=v₂/v₁ definícióból m=v₂ adódik, azaz  ​\( \vec{v}(1,m) \)​v(1; m).
Ezt felhasználva az egyenes irányvektoros  v₂x-v₁y=v₂x₀-v₁y₀ egyenletében: mx-y=mx₀-y₀.

Ezt rendezve: y-y₀=m(x-x₀) alakot kapjuk. Ezt nevezzük az egyenes iránytényezős alakjának.

Kiegészítés:

A fenti egyenletet y-ra rendezve: y=m⋅x+y₀-mx₀.

Ez az adott P₀(x₀;y₀) ponton átmenő és adott m=v₂/v₁ (v₁≠0) meredekségű egyenes egyenlete

Ha itt az y₀-mx₀ tagot b-vel jelöljük, akkor az egyenes egyenlete y=mx+b alakú lesz.
Itt az m iránytangens (meredekség) az x együtthatója, a b állandó pedig megmutatja, hogy hol metszi az egyenes az y tengelyt.