A határozott integrál

A határozott integrál szemléletes fogalma

Tekintsük egy adott intervallumon korlátos f:[a;b]→ℝ;f(x) függvényt!

Osszuk fel az [a;b] intervallumot „n” részre! Az nem lényeges, hogy egyenlő részek legyenek. (a=x₀; x₁; x₂; …;x_n=b).

A parabolikus háromszöghöz hasonlóan fogunk eljárni, a kétoldali közelítés módszerét fogjuk alkalmazni.

Képezzük az adott beosztáshoz tartozó alsó közelítő összegeket:​

\[ s_{n}=m_{1}·\left(x_{1}-x_{0}\right) +m_{2}·\left(x_{2}-x_{1}\right)+…+m_{i}·\left(x_{i}-x_{i-1}\right)+…+m_{n}·\left(x_{n}-x_{n-1}\right)​. \]

Ebben a kifejezésben m_i jelenti az adott (x_i-1;x_i) részintervallumon a függvényértékek alsó határát. (Az alsó korlátok legnagyobbikát, infimumát) Ilyen biztosan van, hiszen feltételeztük, hogy az adott függvény korlátos az [a;b] intervallumon.

És ugyancsak képezzük az adott beosztáshoz tartozó felső közelítő összegeket:​

\[ S_{n}=M_{1}·\left(x_{1}-x_{0}\right) +M_{2}·\left(x_{2}-x_{1}\right)+…+M_{i}·\left(x_{i}-x_{i-1}\right)+…+M_{n}·\left(x_{n}-x_{n-1}\right).​ \]

Ebben a kifejezésben M_i jelenti az adott (x_i-1;x_i)  részintervallumon a függvényértékek felső határát. (A felső korlátok legkisebbikét, szuprémumát.) Ilyen biztosan van, hiszen feltételeztük, hogy az adott függvény korlátos az [a;b] intervallumon.

Megjegyzés: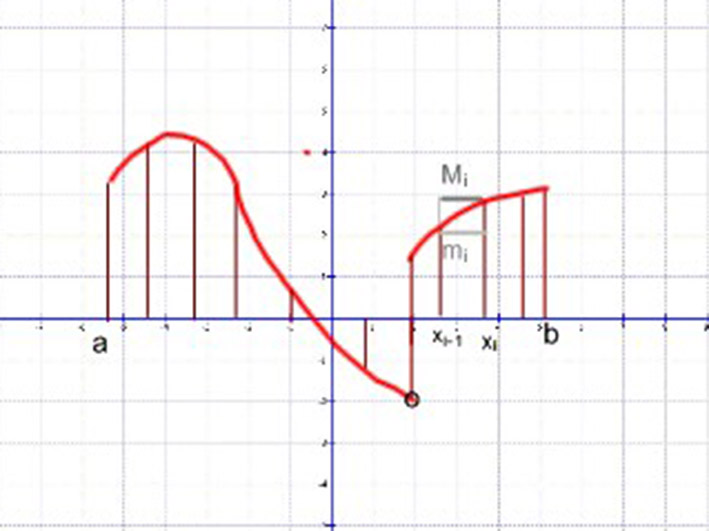

1. A fenti kifejezésekben szereplő összegek egyes tagjai nem feltétlenül pozitív értékek. Ha ezeket terület értékekként kezeljük, akkor előjelet kell társítani hozzá. Azaz az x tengely alatti területekhez negatív értéket rendelünk.

2. A függvény folytonossága nem szükséges, de elégséges feltétel!
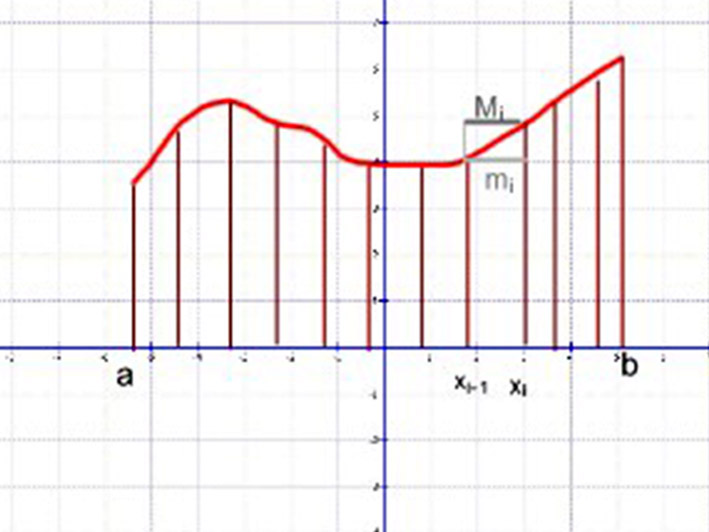
Ha a felosztást finomítjuk, azaz az „n” értékét növeljük akkor a részintervallumok hossza a nullához tart, ugyanakkor az alsó összeg („s_n”) értéke nem csökken, a felső összeg („S_n”) pedig nem nő. És belátható, hogy bármely „n”-hez alsó összeg nem lehet nagyobb bármelyik felső összegnél: s_n≤S_n. Egyenlőség lehetséges, gondoljunk a konstans függvény esetére.

Definíció:

Az [a; b] intervallumon korlátos „f” függvény integrálható, ha csak egyetlen olyan szám található, amely az összes alsó és felső összeg közé esik. Ezt az egyetlen számot nevezzük az „f” függvény [a; b] intervallumon vett határozott integráljának. (Riemann-féle integrál).  ​\( lim_{ nx \to \infty }s_{n}=\lim_{ nx \to \infty }S_{n}=I=\int_{a}^{b}{f(x)dx } \)​.

Jelölés: ​\( \int_{a}^{b}{f(x)dx } \). Kiolvasva: „Integrál „a”-tól „b”-ig f(x) dx.

Megjegyzés:

 ∫ egy elnyújtott S betű, a latin „summa” szó első betűje és Leibniz vezette be. A „dx” „csak” egy szimbólum, azt jelképezi, hogy a kétoldali közelítések alkalmával a függvény értékét megszoroztuk az egyes intervallumok hosszával.

Definíció:

Ha az f(x) függvény értelmezve van az „a” pontban, akkor ​\( \int_{a}^{a}{f(x)dx }=0 \)​.

Példa:

A parabolikus háromszög területének meghatározásakor a sorozatok határértékével számolva határoztuk meg az f(x)=x² függvény Riemann-integráljának (a görbe alatti terület) értékét: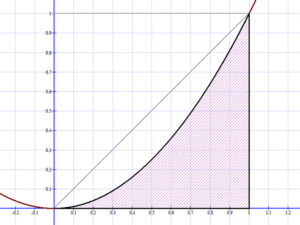

​\( \int_{0}^{1}{x^2dx}=\frac{1}{3} \)​.

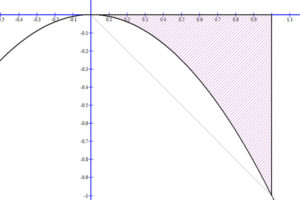Hasonlóan a g(x)=-x² függvény és az x tengely [0; 1] intervalluma által meghatározott terület értéke:

​\( \int_{0}^{1}{(-x^2)dx}=-\frac{1}{3} \)​.

Természetesen létezik könnyebb eljárás – éppen az integrálás segítségével –  egy függvény görbe alatti területének meghatározására.