Már az ókori matematikusokat (Például Arkhimédész, Hippokratész, Eratoszthenész) izgatta az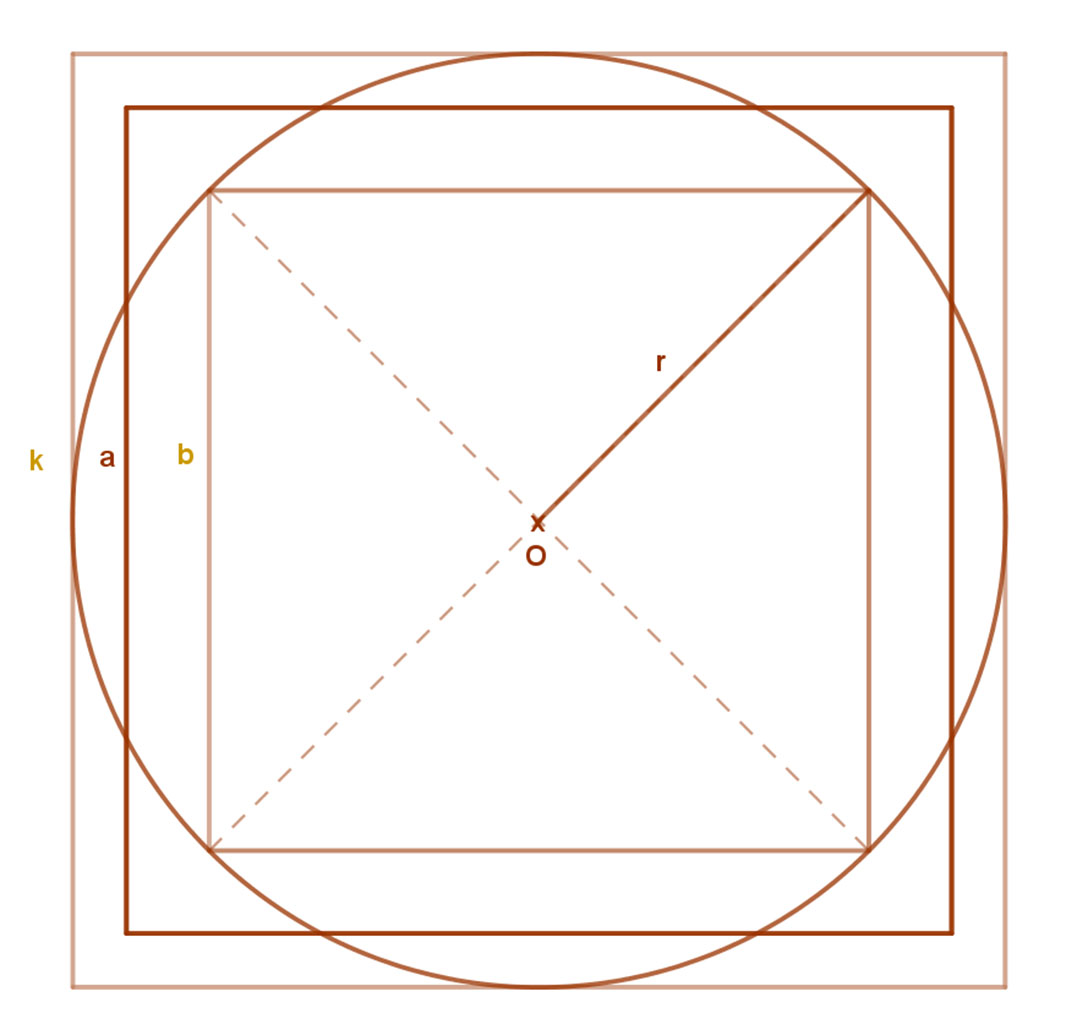 
a kérdés, hogyan lehet egy adott kör területével egyenlő területű négyszöget szerkeszteni. A körbe írt és a köré kör írt négyzetekkel próbálták a kör területét behatárolni.
Ma már közismert, hogy a kör területe=r2π és az is közismert, hogy a π egy irracionális szám. Ennek természetét és értékének meghatározását sokan próbálták.
Arkhimédész a π értékét a körbe írt 96 (!) oldalú szabályos sokszög területével közelítette meg. Ő az un. kimerítés módszerét alkalmazta, amely lényegében a mai középiskolai kétoldalú közelítés módszeréhez hasonlít.
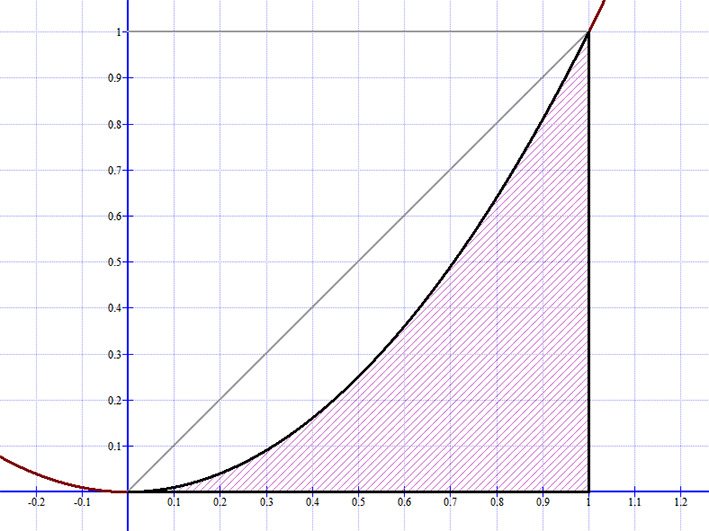
Parabolaív által határolt parabolikus háromszög területe
Ábrázoljuk az y=x2 parabolát a [0; 1] intervallumon erős nagyítással!
A parabolikus háromszöget egy parabola ív, az „x” tengely és egy az „y” tengellyel párhuzamos egyenes határol.
Ennek területe biztosan kisebb, mint 0.5 területegység, hiszen kisebb, mint az 1 x 1-es négyzet területének a fele.
Most is hasonlóan járjunk el, mint a „régiek”. Alkalmazzuk a kétoldali közelítés módszerét.
Jelöljük ki a parabolán az x = 0.2; 0.4; 0.6; és a 0.8 abszcisszájú pontokat!
Ezekből a pontokból az „x” tengellyel párhuzamos egyenesekkel képezzünk a parabola görbe alatti téglalapokat (beírt téglalapok), valamint a parabolaívhez köréírt téglalapokat!
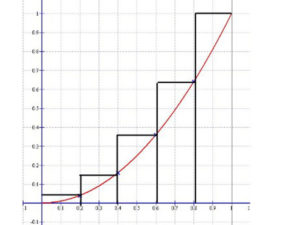
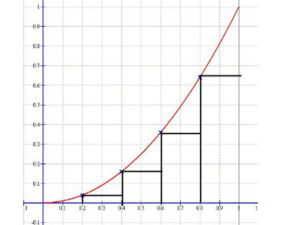
Ismételjük meg az eljárást a beírt és a köré írt téglalapokkal. Persze ezt általánosíthatjuk.
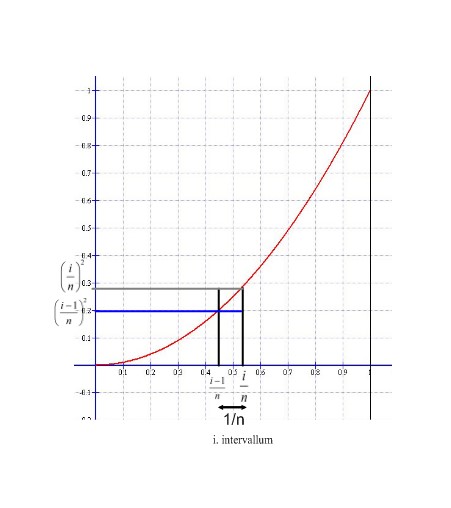
Legyen a beosztás mértéke 1/n. Ekkor minden téglalap egyik oldala 1/n.
Az i.-ik osztáshoz tartozó beírt téglalap másik oldala ekkor [(i-1)/n]2, így a téglalap területe: \( t_{b}=\frac{1}{n}·\left(\frac{i-1}{n}\right)^2 \).
Míg az i. intervallumhoz tartozó köré írt téglalap területe: \( t_{k}=\frac{1}{n}·\left(\frac{i}{n}\right)^2 \).
Összegezzük a beírt és a köré írt téglalapok területeit!
A beírt téglalapok területeinek az összege: \( s_{n}=\frac{1}{n^3}·\left\{ 1^2+2^2+3^2+…+(n-1)^2 \right\} \).
A köré írt téglalapok területinek összege: \( S_{n}= \frac{1}{n^3}·\left\{ 1^2+2^2+3^2+…+n^2 \right\} \).
A parabolaív alatti terület nyilván a két érték között van.
\[ \frac{1}{n^3}·\left\{ 1^2+2^2+3^2+…+(n-1)^2 \right\}=s_{n}<T<S_{n}=\frac{1}{n^3}·\left\{ 1^2+2^2+3^2+…+n^2 \right\} \]
Felhasználva, hogy az első „k” darab pozitív egész szám négyzetösszege zárt alakban: \( 1^2+2^2+3^2+…+k^2 =\frac{k(k+1)(2k+1)}{6} \). Ez teljes indukcióval bizonyítható.
Ezt behelyettesítve az egyenlőtlenségek zárójelei között szereplő négyzetösszegere:
\[ \frac{(n-1)n(2n-1)}{6n^3}=s_{n}<T<S_{n}=\frac{n(n+1)(2n+1)}{6n^3} \]
Átalakítás után:
\[ \left( 1-\frac{1}{n} \right)·\left( \frac{1}{3}-\frac{1}{6n} \right)=s_{n}<T<S_{n}=\left( 1 +\frac{1}{n} \right)·\left( \frac{1}{3}+\frac{1}{6n} \right) \]
Az „n” értékét (a felosztás mértékét) minden határon túl növelve a beírt és a köré írt téglalapok területeire kapott kifejezések határértékei:
\[ \lim_{ n \to \infty }\left( 1-\frac{1}{n} \right)·\left( \frac{1}{3}-\frac{1}{6n} \right)=\frac{1}{3} \; és \; \lim_{ n \to \infty }\left( 1+\frac{1}{n} \right)·\left( \frac{1}{3}+\frac{1}{6n} \right)=\frac{1}{3} \].
Ezt felhasználva a beírt, a parabolikus háromszög és a köré írt téglalapok területire vonatkozó egyenlőtlenségek:
\[ \frac{1}{3}<T<\frac{1}{3} \]
A sorozatok határértékeire vonatkozó un. „rendőr-elv” szerint az pontosan azt jelenti, hogy a parabolikus háromszög területe:
\[ T=\frac{1}{3} \].
Comments are closed, but trackbacks and pingbacks are open.