A 100 m-es gyorsúszás döntőjében 8-an indulnak. Hányféleképpen lehet az érmeket kiosztani, ha tudjuk, hogy az első három helyezett kap érmet?
Az ilyen típusú feladatoknál természetesen nem mindegy, hogy kik és milyen sorrendben állnak a dobogón, kapják az érmeket.
Kiválasztás: kik állnak a dobogón.
Sorrend: milyen sorrendben értek célba.
Készítsünk most is egy kis modellt!
| I. helyezett. | II. helyezett. | III. helyezett. |
| 8 lehetőség. | 7 lehetőség. | 6 lehetőség. |
Tehát a lehetőségek száma: 8⋅7⋅6=336.
A feladatot általánosan megfogalmazva:
Hányféleképpen választhatunk ki n darab különböző „tárgyból” k darabot akkor, ha a kiválasztás sorrendje is számít (k≤n)?
Definíció:
Ha egy n elemű halmaz elemeiből úgy képezünk k hosszúságú elemsorozatokat (k≤n), úgy hogy azok sorrendje is fontos és minden elemet csak egyszer választunk ki, akkor ezt az eljárást variálásnak mondjuk.
Az így kapott elemsorozatokat (egy adott kiválasztás adott elrendezését) ismétlés nélküli variációnak nevezzük. Az összes lehetőségek számát, n elem k-ad osztályú variációnak számát \( {V^k_{n}} \)-val jelöljük.
A variációnál tehát kiválasztás és sorrend is szerepel
Tétel:
„n” különböző elem k-ad osztályú variációinak száma: \( {V^k_{n}}=\frac{n!}{\left( n-k \right)! } \)
Bizonyítás:
| 1. hely | 2. hely | 3. hely | …. | (k-1). hely | k. hely |
| n lehetőség | (n-1) lehetőség | (n-2) lehetőség | …. | n-(k-1)+1=n-k+2 lehetőség |
n-k+1 lehetőség |
Az összes lehetőségek számát az egyes helyekre jutó lehetőségek szorzata adja:
\( {V^k_{n}} \)=n(n-1)(n-2)…(n-k+2)(n-k+1).
Ez tehát egy k tényezős szorzat, n-től kezdve lefelé összeszorozzuk a pozitív egész számokat n-k+1-ig.
Alakítsuk át a kapott kifejezést úgy, hogy a jobb oldali szorzatot folytassuk lefelé egészen 1-ig, azaz a kifejezést szorozzuk meg (n-k)(n-k-1)(n-k-2)…3⋅2⋅1 -gyel. Hogy a kifejezés értéke ne változzon ezért ugyanezekkel a tényezőkkel osztanunk is kell.
Tehát: 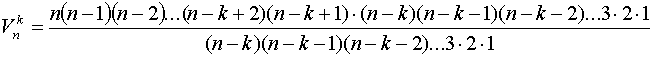
A bővítésnél alkalmazott (n-k)(n-k-1)(n-k-2)…3⋅2⋅1 szorzat éppen (n-k)!-sal egyenlő. Ezzel a művelettel, n faktoriálissal (n!) a permutációk számánál találkoztunk.
A bővítésnél alkalmazott (n-k)(n-k-1)(n-k-2)…3⋅2⋅1 szorzat éppen (n-k)!-sal egyenlő. Ezzel a művelettel, n faktoriálissal (n!) a permutációk számánál találkoztunk.
Így n elem k-ad osztályú variációinak a számára a következő alakot kaptuk: \( {V^k_{n}}=\frac{n!}{\left( n-k \right)! } \), ahol k≤n.
És ezt kellett bizonyítani.
Feladat:
Egy 35-ös létszámú osztályban 7 különböző könyvet sorsolnak ki. Hányféleképpen történhet a könyvek szétosztása, ha
a) egy tanuló csak egy könyvet kaphat;
b) egy tanuló több könyvet is kaphat?
(Összefoglaló feladatgyűjtemény 4077. feladat.)
Megoldás:
a) 35 tanulóból kell 7 főt kiválasztani és mivel a könyvek különbözőek, nem mindegy a sorrend sem. A lehetőségek száma 35 elem 7-ed osztályú variációinak a számával egyenlő.
\( {V^7_{35}}=\frac{35!}{\left( 35-7 \right)! }=\frac{35!}{28!} \)
A számlálóban és a nevezőben azonban óriási számok szerepelnek. Így sok esetben elegendő ezt a kifejezést, mint eredményt közölni. Ha azonban az érték kiszámítására is szükség van, akkor sokszor egyszerűbb a 7 tényezős szorzat felírása:
\( {V^7_{35}} \)=35⋅34⋅33⋅32⋅31⋅30⋅29=33 891 580 800=3,38915808*1010. Vagyis több mint 33 milliárd!
b) Ha azonban egy tanuló több könyvet is kaphat, akkor 35 elem 7-ed osztályú ismétléses variációjáról beszélünk.
\( {V^{7,(i)}_{35}}=35^{7} \)=35⋅35⋅35⋅35⋅35⋅35⋅35=357=64339296875=6,4339296875*1010. Vagyis a lehetőségek száma több mint 64 milliárd.
Általában:
Ha egy n elemű halmaz elemeiből úgy képezünk k hosszúságú elemsorozatokat (k≤n), úgy hogy azok sorrendje is fontos és minden elemet többször is kiválasztunk ki, akkor ismétléses variációról beszélünk.
Tétel:
„n” elem „k” tagú ismétléses variációinak száma nk. Azaz: \( {V^{k,(i)}_{n}}=n^{k} \).


Comments are closed, but trackbacks and pingbacks are open.