 Definíció:
Definíció:
Egy alakzat középpontosan szimmetrikus, ha létezik olyan pont, amelyre történő tükrözésnél az alakzat képe önmaga.
Középpontosan szimmetrikus síkbeli alakzatok:
1. Középpontosan szimmetrikus háromszög nem létezik.
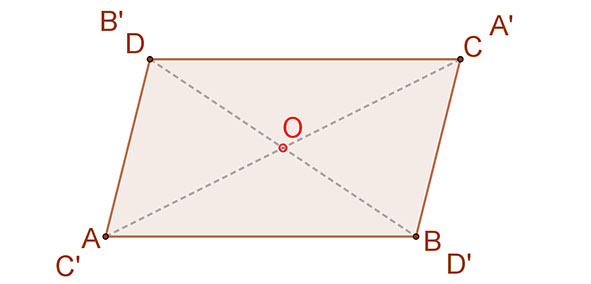
2.  Középpontosan szimmetrikus négyszögek a paralelogrammák.
Középpontosan szimmetrikus négyszögek a paralelogrammák.
3. K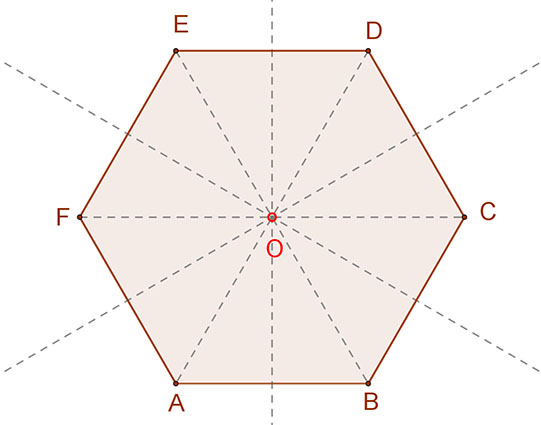 özéppontosan szimmetrikus sokszögek a páros számú szabályos sokszögek.
özéppontosan szimmetrikus sokszögek a páros számú szabályos sokszögek.
4. Természetesen középpontosan szimmetrikus a kör is.
 Definíció:
Definíció:
Egy síkbeli alakzat tengelyesen szimmetrikus, ha az alakzat síkjában létezik olyan tengely, amelyre történő tükrözésnél az alakzat képe önmaga.
Tengelyesen szimmetrikus síkbeli alakzatok:
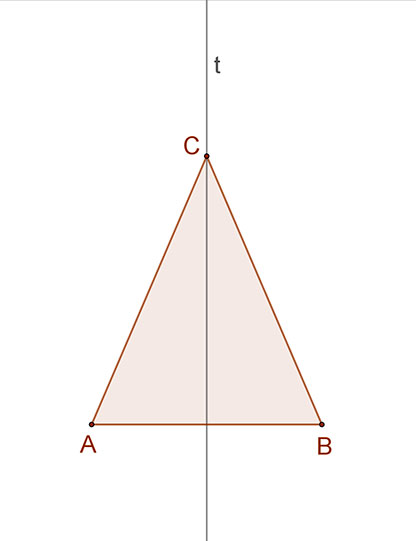 1. Tengelyesen szimmetrikus háromszögek az egyenlőszárú háromszögek.
1. Tengelyesen szimmetrikus háromszögek az egyenlőszárú háromszögek.
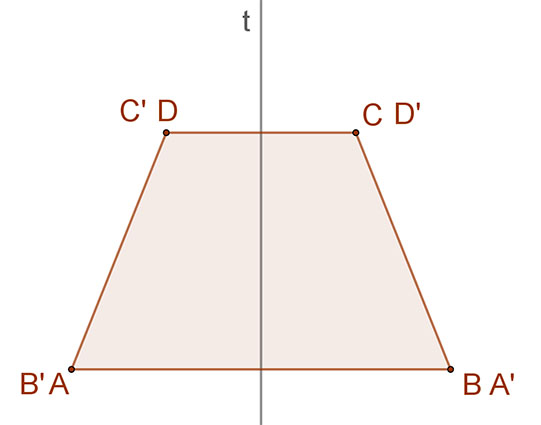
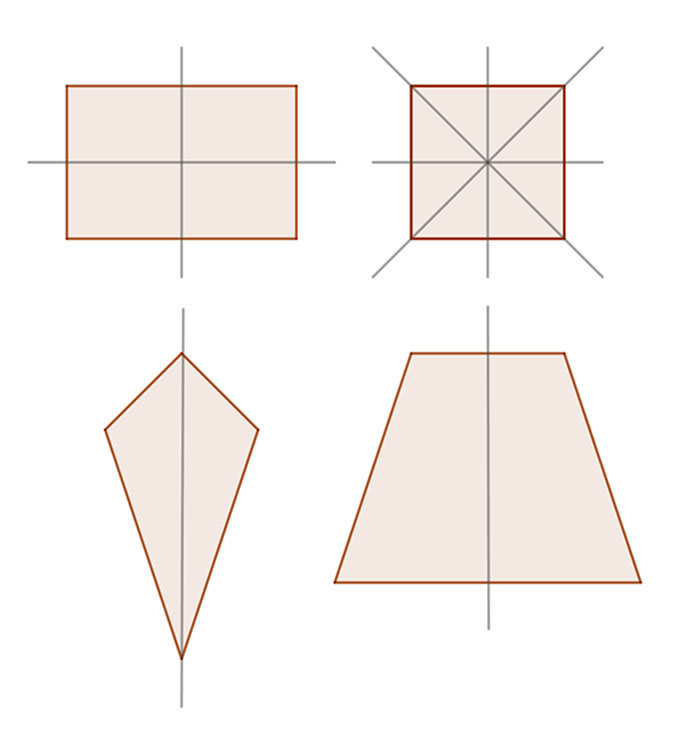 2. Tengelyesen szimmetrikus négyszögek: téglalap, négyzet és a deltoid, valamint a szimmetrikus trapéz. (húrtrapéz.)
2. Tengelyesen szimmetrikus négyszögek: téglalap, négyzet és a deltoid, valamint a szimmetrikus trapéz. (húrtrapéz.)
Téglalapnak 2 db., a négyzetnek 4 db., a deltoidnak és a húrtrapéznak 1 db szimmetria tengelye van.
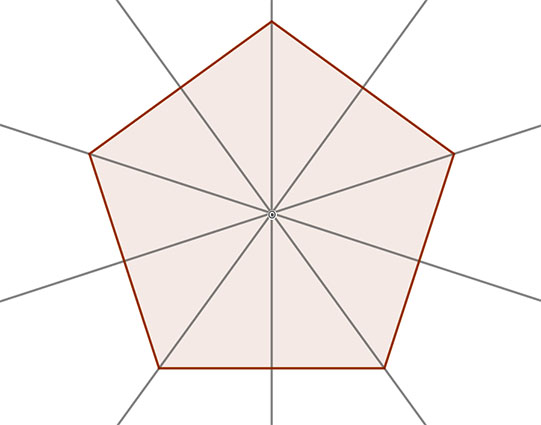 3. Minden szabályos sokszög tengelyesen szimmetrikus. Az „n” oldalú szabályos sokszögnek „n” db szimmetria tengelye van.
3. Minden szabályos sokszög tengelyesen szimmetrikus. Az „n” oldalú szabályos sokszögnek „n” db szimmetria tengelye van.
4. Természetesen a kör is tengelyesen szimmetrikus. Minden, a kör középpontján áthaladó egyenes szimmetria tengely. Tehát a körnek végtelen sok szimmetria tengelye van.


Comments are closed, but trackbacks and pingbacks are open.