Tétel:
Vektorok skaláris szorzata a vektorok összeadására nézve tagolható (disztributív).
Formulával: Minden \( \vec{a} \), \( \vec{b} \) és \( \vec{c} \) vektor esetén \( (\vec{a}+\vec{b})·\vec{c}=\vec{a}·\vec{c}+\vec{b}·\vec{c} \).
Bizonyítás:
1. Ha a \( \vec{c} \) vektor nullvektor, azaz |\( \vec{c} \)|=0, akkor az állítás igaz, ugyanis a skaláris szorzat definíciója szerint bármely vektornak, így az \( (\vec{a}+\vec{b}) \) vektornak is a nullvektorral vett skaláris szorzata=0, ezért az állítás baloldala \( (\vec{a}+\vec{b}) \)⋅0=0. Másrészt az állítás jobb oldala: \( \vec{a} \)⋅0+\( \vec{b} \) ⋅0=0. Tehát az állítás igaz.
2. Ha a \( \vec{c} \) vektor nem nullvektor, akkor \( \vec{c} \) felírható az abszolút értékének és a vele párhuzamos egységvektornak a szorzataként. Azaz \( \vec{c} \)=|\( \vec{c} \)|⋅\( \vec{e} \).
Így elegendő \( (\vec{a}+\vec{b})·\vec{e}=\vec{a}·\vec{e}+\vec{b}·\vec{e} \) állítást belátnunk. Hiszen ha ezt beszorozzuk |\( \vec{c} \)|-vel, az eredeti állítást kapjuk.
A bizonyításhoz fel fogjuk használni a következőt:
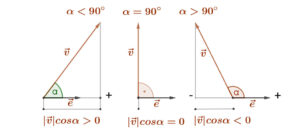A skaláris szorzat definíciója alapján belátható, hogy egy vektornak és egy egységvektornak a skaláris szorzata az adott vektornak az egységvektor egyenesére eső merőleges vetületének az előjeles hosszát adja. (Ezt hívjuk skalárvetületnek.) \( \vec{v}·\vec{e}=|\vec{v}|·cos(α) \).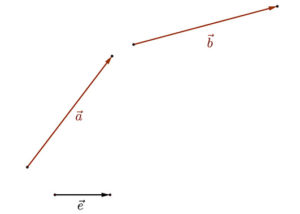
Tekintsünk most adottnak az \( \vec{a} \), \( \vec{b} \) és \( \vec{e} \) vektorokat, ahol tudjuk, hogy |\( \vec{e} \)|=1.
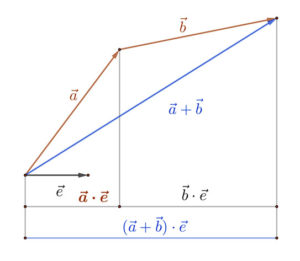Toljuk a \( \vec{b} \) vektort az a vektor végpontjába. Az egymáshoz csatlakoztatott \( \vec{a} \) és \( \vec{b} \) vektoroknak az \( \vec{e} \) egységvektor meghosszabbítására eső skalárvetületük összege megegyezik az \( \vec{a}+\vec{b} \)összegvektor ugyaezen \( \vec{e} \) vektorra vonatkozó skalárvetületével.
Tehát : \( (\vec{a}+\vec{b})·\vec{e}=\vec{a}·\vec{e}+\vec{b}·\vec{e} \).
Ezt |\( \vec{c} \)| számmal végigszorozva, a bizonyítandó állítást kapjuk.
\( |\vec{c}|·\vec{e}·\vec{a}+|\vec{c}|·\vec{e}·\vec{b}=(\vec{a}+\vec{b})·|\vec{c}|·\vec{e} \).
Mivel \( |\vec{c}|·\vec{e}=\vec{c} \), ezért \( \vec{a}·\vec{c}+\vec{b}·\vec{c}=(\vec{a}+\vec{b})·\vec{c} \)
Ezt kellett igazolni.
Comments are closed, but trackbacks and pingbacks are open.