Hippokratész ókori görög matematikus sokat foglalkozott körívek és egyenesek által határolt síkidomok területének meghatározásával. A most következő példa, Hippokratész „holdacskái” egy konkrét példa arra, hogy görbe vonalakkal határolt síkidom adott esetben és adott értelemben négyszögesíthető.
Feladat:
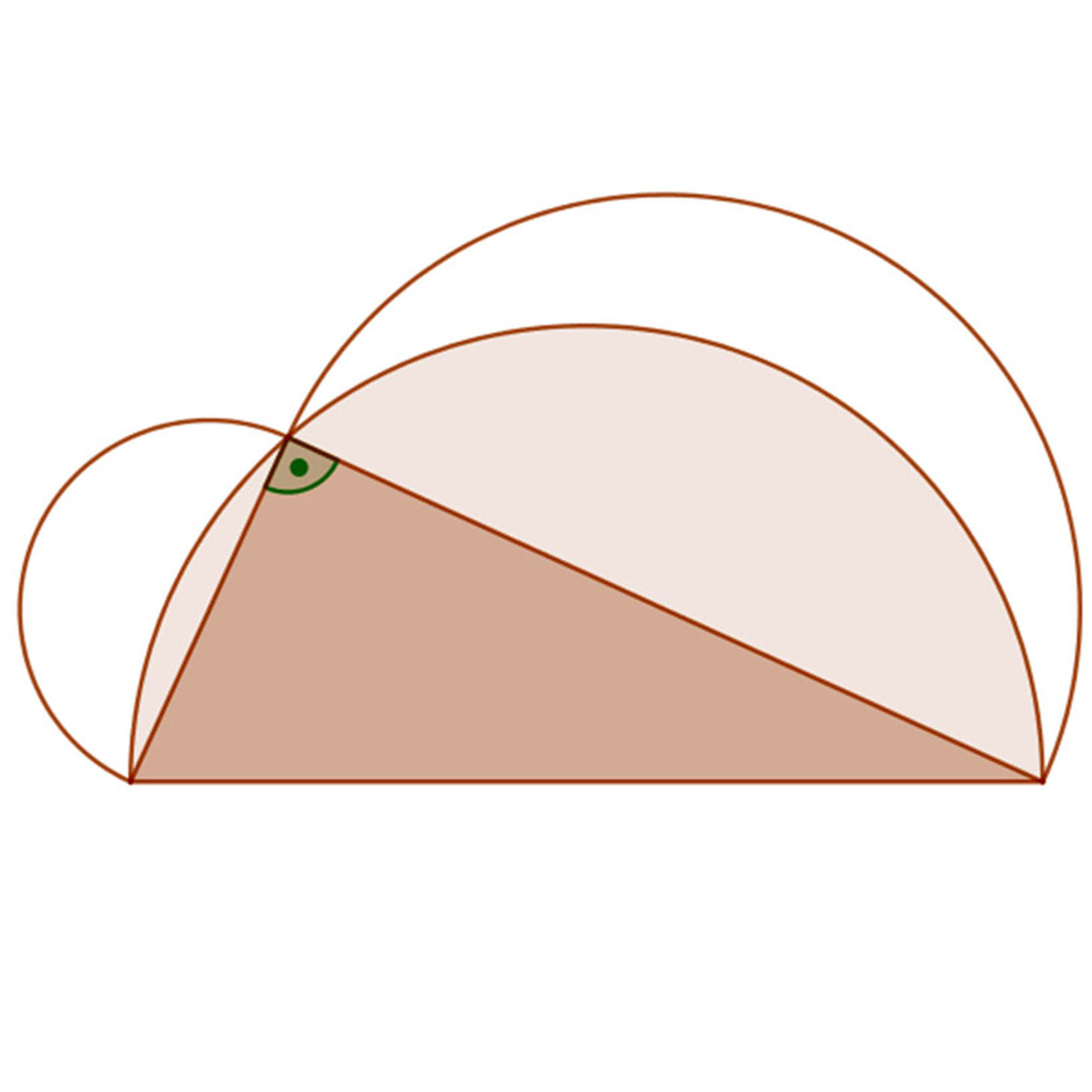
Az ábrán lévő holdacskákat a derékszögű háromszög oldalai fölé szerkesztett félkörök határolják. Bizonyítsuk be, hogy a holdacskák területének összege a háromszög területével egyenlő.
Ez a feladat a középiskolákban rendszeresített „Geometriai feladatok gyűjteménye I.” kötetében szerepel az 1523. számon.
Megoldás:
A holdak területét megkapjuk, ha a befogók fölé emelt félkörök területéből kivonjuk azoknak a körszeleteknek a területét, amelyeket úgy kapunk, hogy az átfogó fölé emelt félkör területéből kivonjuk a háromszög területét.
Formulával: Jelöljük a derékszögű háromszög befogóit „a” és „b„, az átfogót pedig „c” változóval.
Ekkor a derékszögű háromszög területe: \( \frac{ab}{2} \), a befogók fölé emelt félkörök területe: \( =\frac{\left(\frac{a}{2} \right)^{2}}{2}·π =\frac{a^{2}}{8}· π \) és \( =\frac{\left(\frac{b}{2} \right)^{2}}{2}·π =\frac{b^{2}}{8}· π \). Az átfogó fölé emelt félkör területe: \( =\frac{\left(\frac{c}{2} \right)^{2}}{2}·π =\frac{c^{2}}{8}· π \).
Így a körszeletek területe: \( \frac{c^{2}}{8}· π-\frac{a·b}{2} \).
Holdak területét tehát megkapjuk, ha befogók fölé emelt félkörök területeinek összegéből kivonjuk a körszeletek területét.
Azaz a holdacskák területe: \( \frac{a^{2}}{8}· π+\frac{b^{2}}{8}· π-\left [\frac{c^{2}}{8}· π-\frac{a·b}{2} \right ] \).
Zárójel felbontása után: \( \frac{a^{2} π }{8}+\frac{b^{2} π }{8}-\frac{c^{2} π }{8}+\frac{ab }{2} \).
Emeljük ki \( \frac{ π }{8} \)-t az első három tagból: \( \frac{ π }{8}\left(a^{2}+b^{2}-c^{2}\right)+\frac{ab}{2} \).
A zárójelben szereplő kifejezés Pitagorasz tétele értelmében nullával egyenlő, ezért a holdacskák területe = \( \frac{ab}{2} \).
És ezt kellett igazolni.


Comments are closed, but trackbacks and pingbacks are open.