Tétel:
A háromszög magasságvonalai egy pontban metszik egymást.
Bizonyítás:
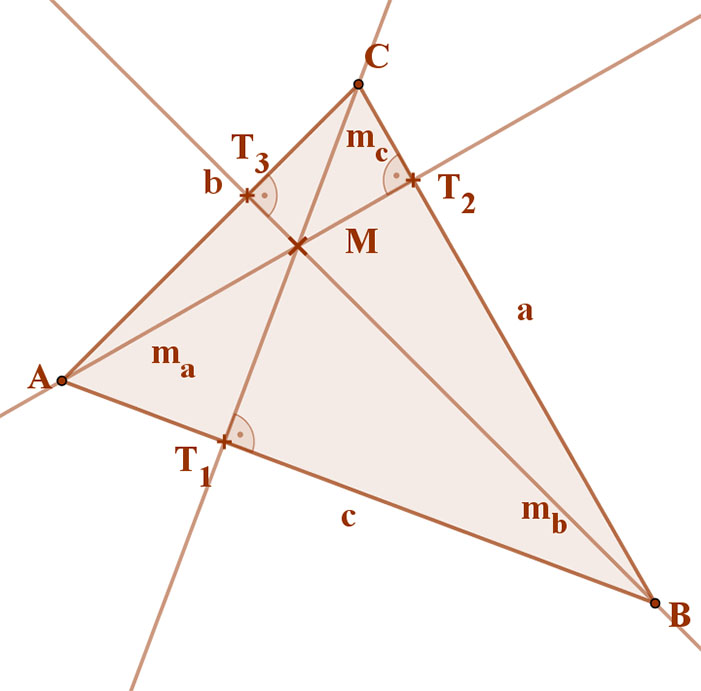
Tekintsük a jobb oldali ábrán az ABC háromszöget. Az a, b és c oldalhoz tartozó magasságokat jelöljük ma, mb, mc-vel.
Azt kell belátnunk, hogy ezek egy pontban metszik egymást.
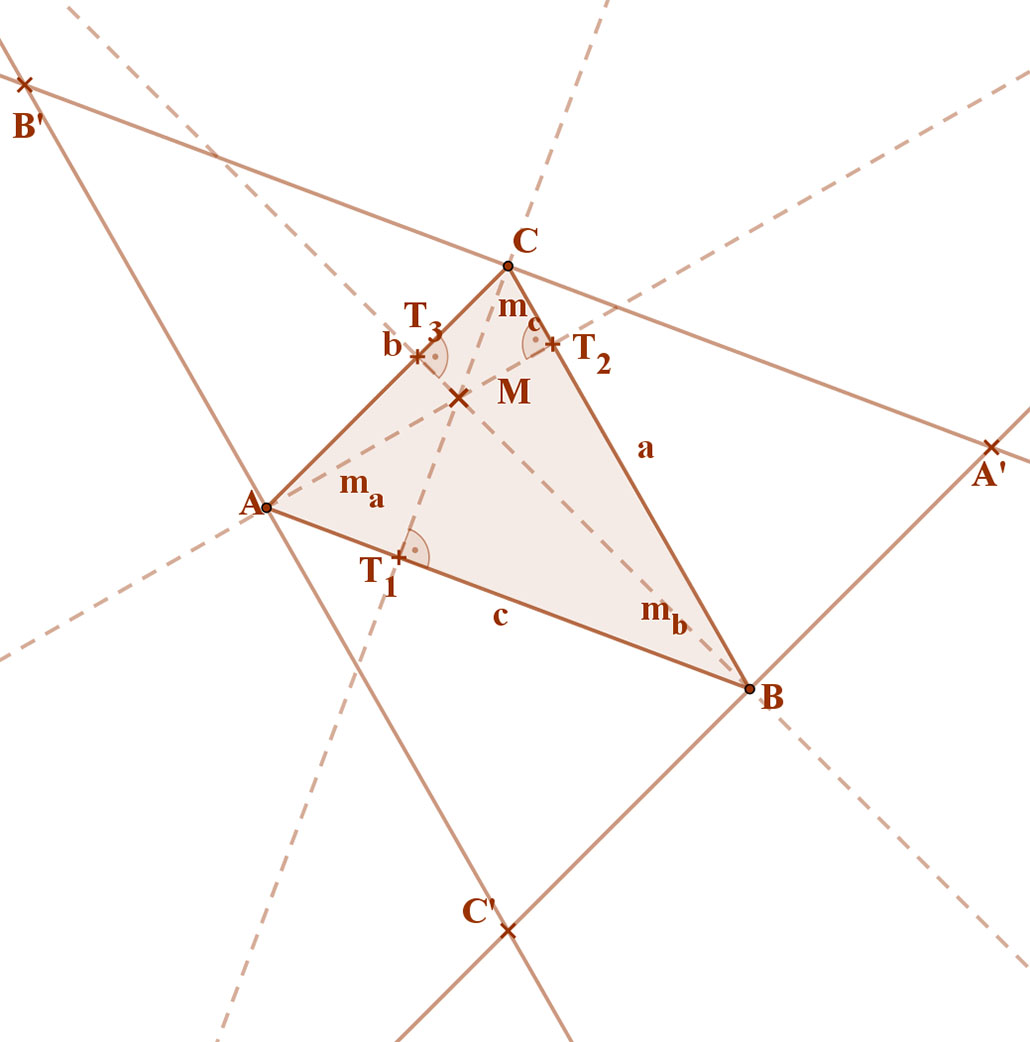
Húzzunk az ABC háromszög egyes csúcsain át párhuzamosokat a szemben lévő oldalakkal. Így kapjuk az A’B’C’ háromszöget. (Ez a „csel”.)
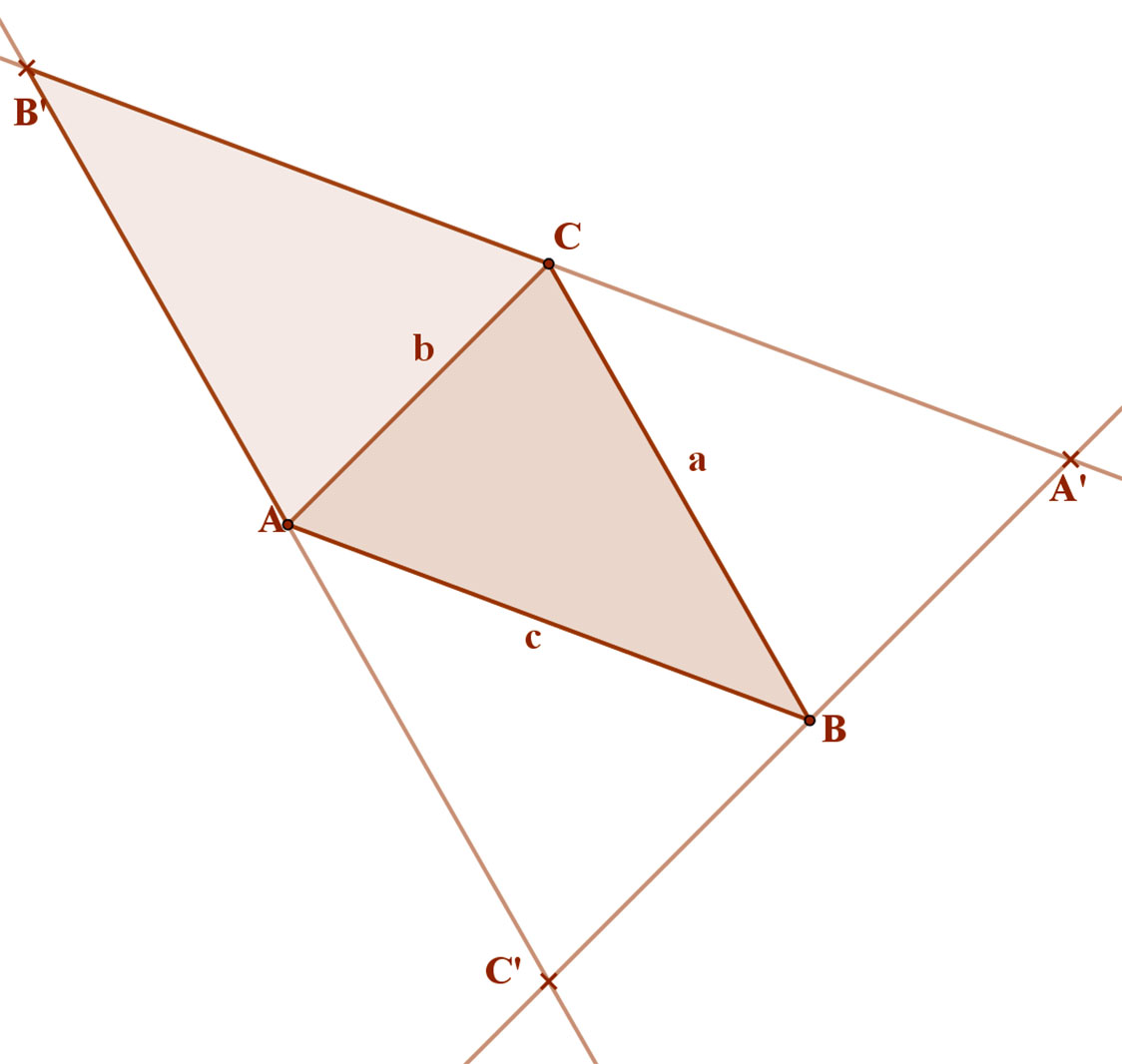
Az ABCB’ négyszög paralelogramma, hiszen oldalai párhuzamosak. Ebből következik, hogy: AB=B’C és BC=AB’.
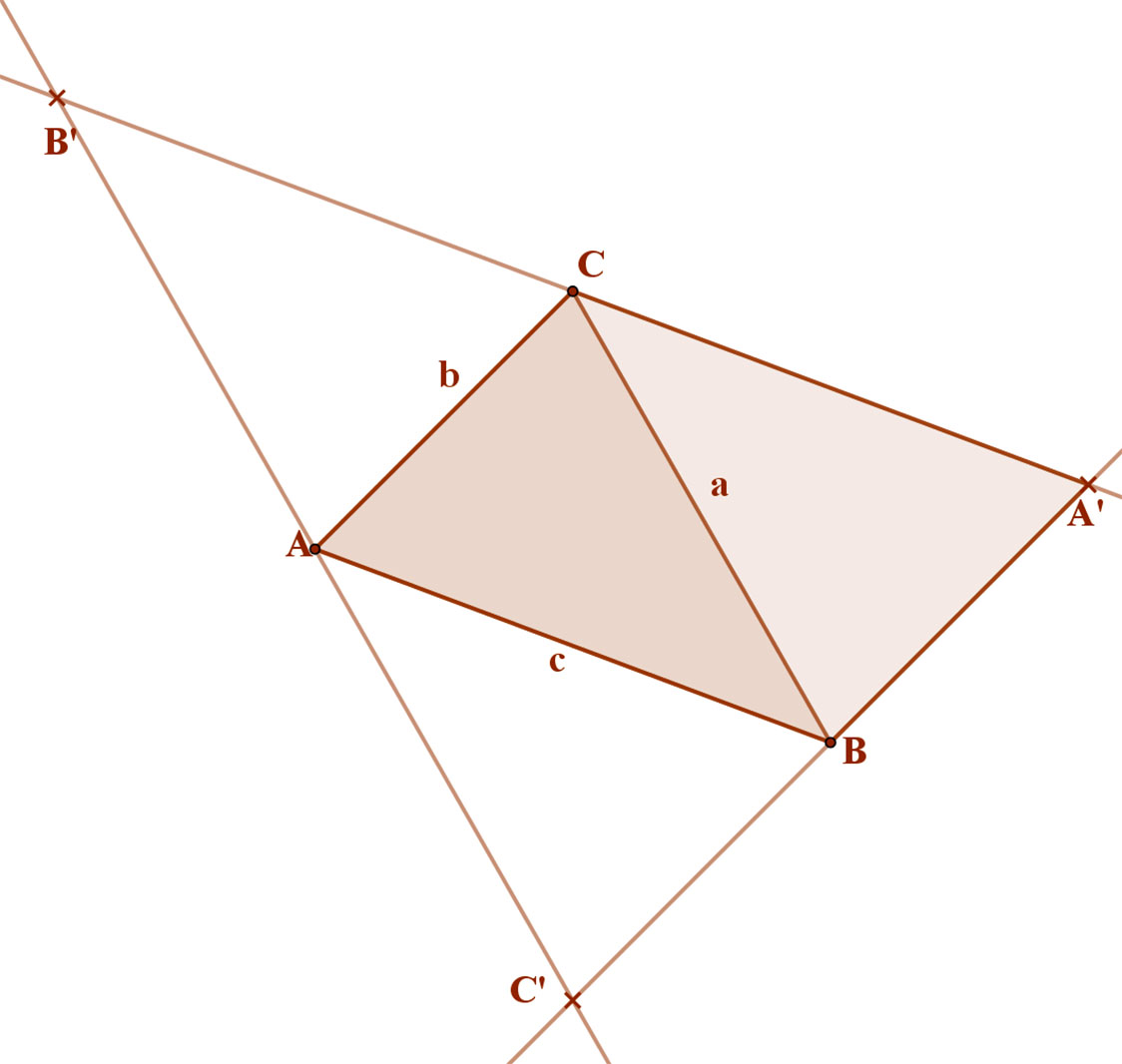
Hasonlóan, az ABA’C négyszög is paralelogramma, ezért: AB=A’C és AC=BA’
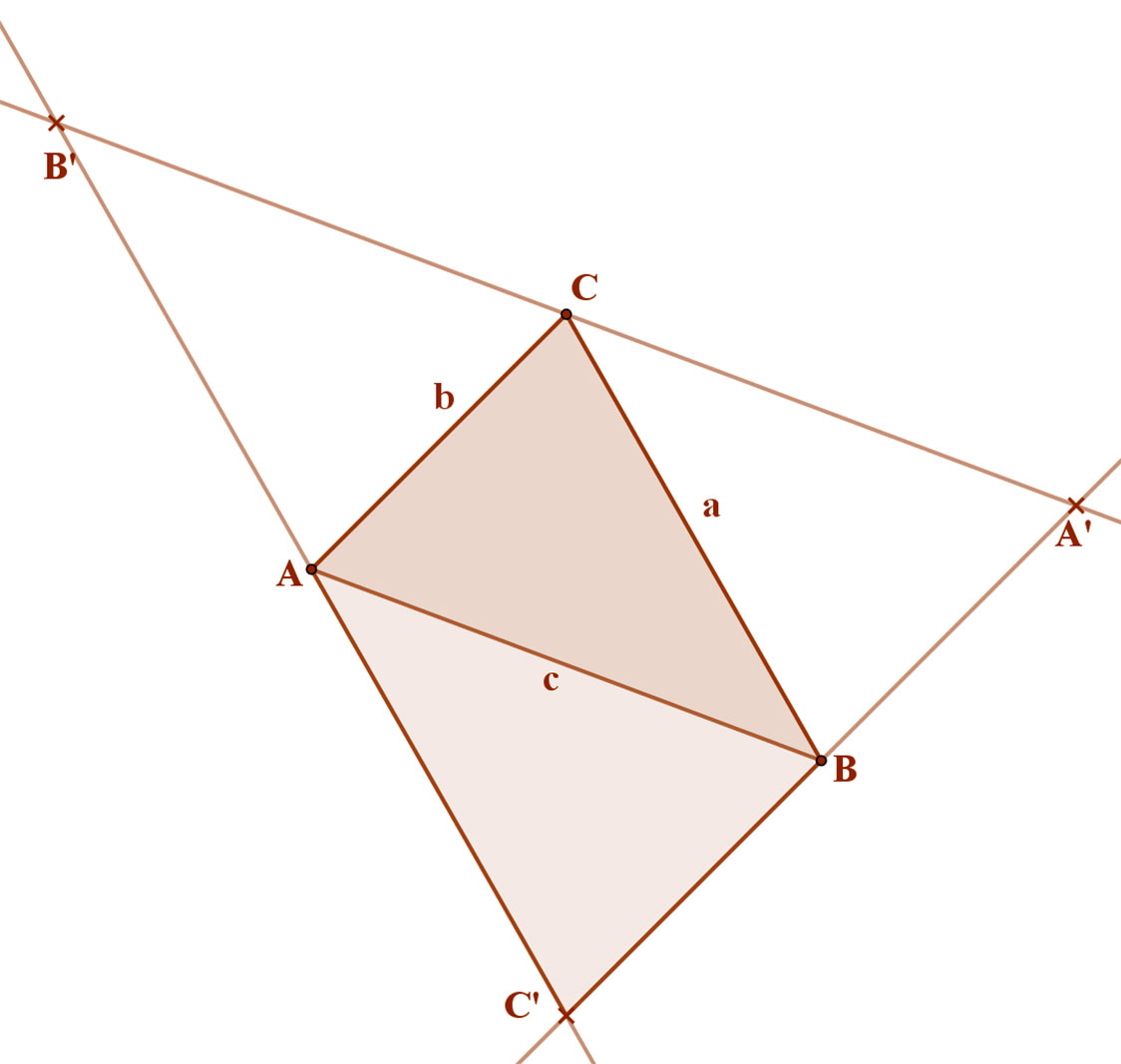
Ugyancsak paralelogramma az AC’BC négyszög, ezért:
AC’=BC és AC=C’B.
Mivel AB szakasz párhuzamos A’B’-vel, és AB=B’C és AB=CA’, ezért AB=A’B’/2. Tehát az AB szakasz középvonala az A’B’C’ háromszögnek. A C pont a B’A’ szakasz felezőpontja.
Az AC szakasz párhuzamos C’A’-vel, és AC=C’B és AC=BA’, ezért AC=A’C’/2. Tehát az AC szakasz középvonala az A’B’C’ háromszögnek. A B pont a C’A’ szakasz felezőpontja.
A CB szakasz párhuzamos a C’B’-vel, és BC=AC’ és BC=AB’, ezért BC=B’C’/2. Tehát a BC szakasz középvonala az A’B’C’ háromszögnek. Az A pont a C’B’ szakasz felezési pontja.
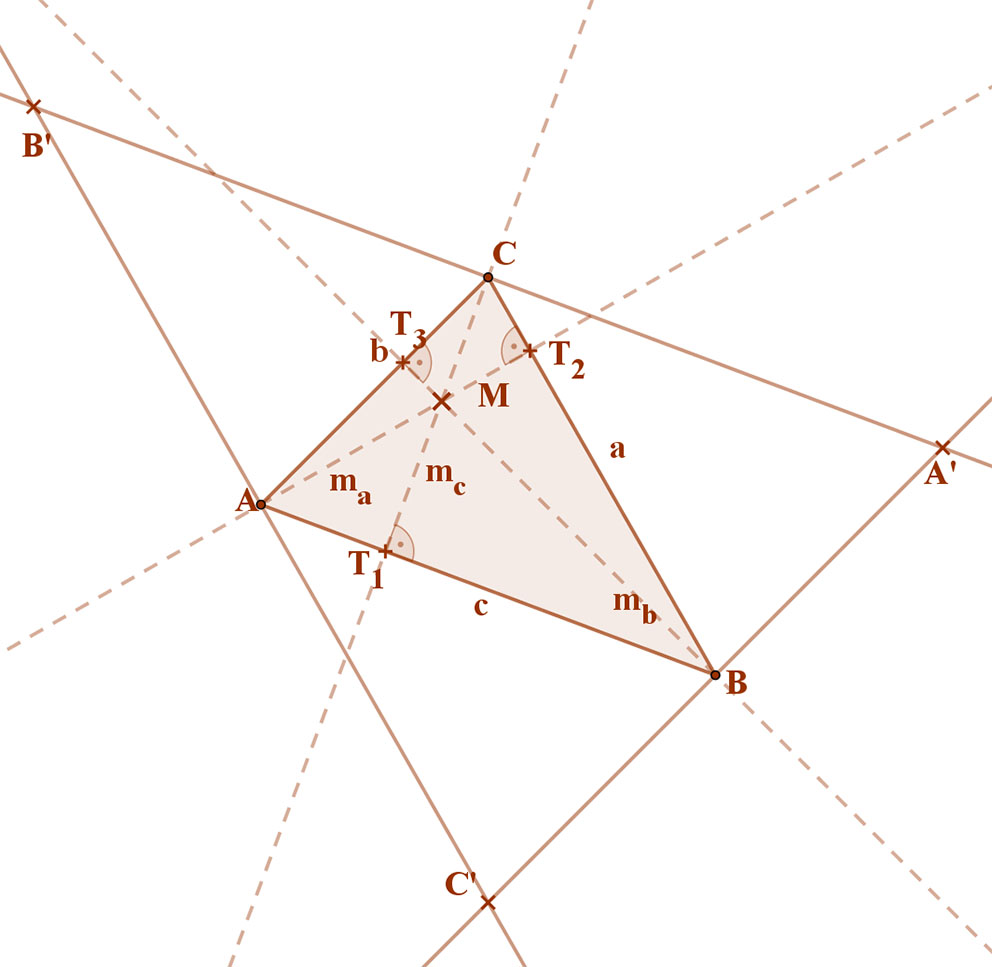
Mivel AB||A’B’, ezért az ABC háromszög mc magasságvonala merőleges A’B’-re.
Mivel AC||A’C’, ezért az ABC háromszög mb magasságvonala merőleges A’C’-re.
Mivel BC||C’B’, ezért az ABC háromszög ma magasságvonala merőleges B’C’-re.
A fentiekből következik, hogy az ABC háromszög ma, mb, mc és mc magasságvonalai oldalfelező merőlegesei az A’B’C’ háromszögnek.
Azt tudjuk, hogy az A’B’C’ háromszög oldalfelezői egy pontban metszik egymást, ebből következik, hogy az ABC háromszög magasságvonalai is egy pontban metszik egymást.
 |
 |
 |
|
Hegyesszögű háromszög esetén magasságvonalainak M metszéspontja a háromszög belsejében van. |
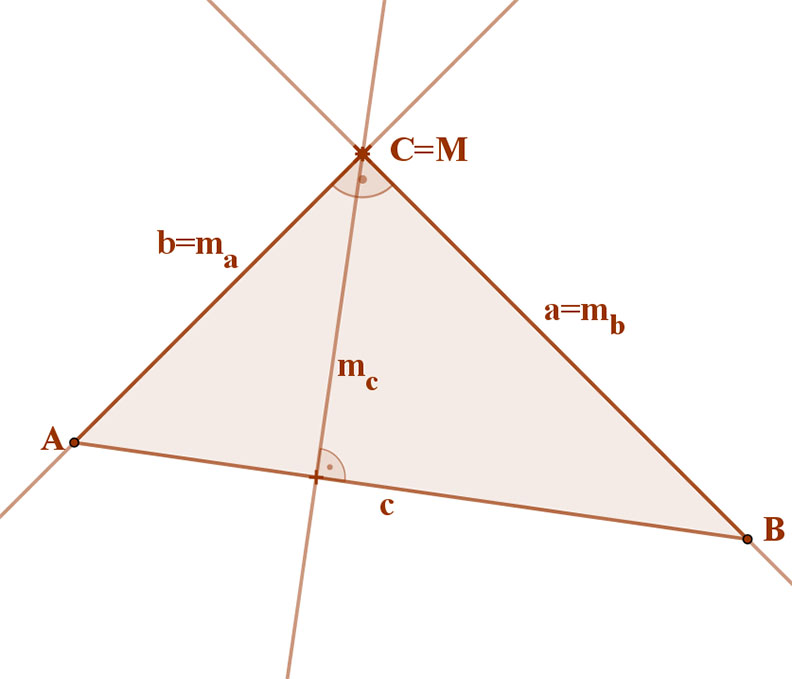
Derékszögű háromszög esetén a háromszög magasságpontja a derékszögnél lévő csúcs. |
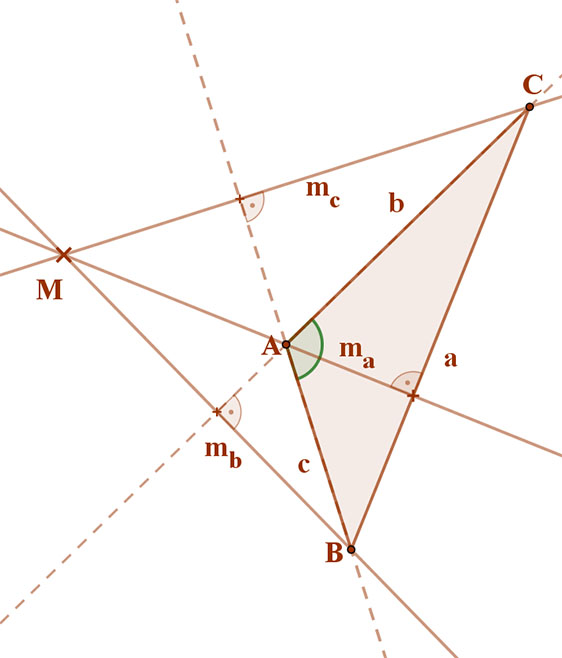
Tompaszögű háromszög esetén pedig a magasságpont a háromszögön kívül van. |
Az alábbi animáción látni lehet a magasságpont helyének változását.
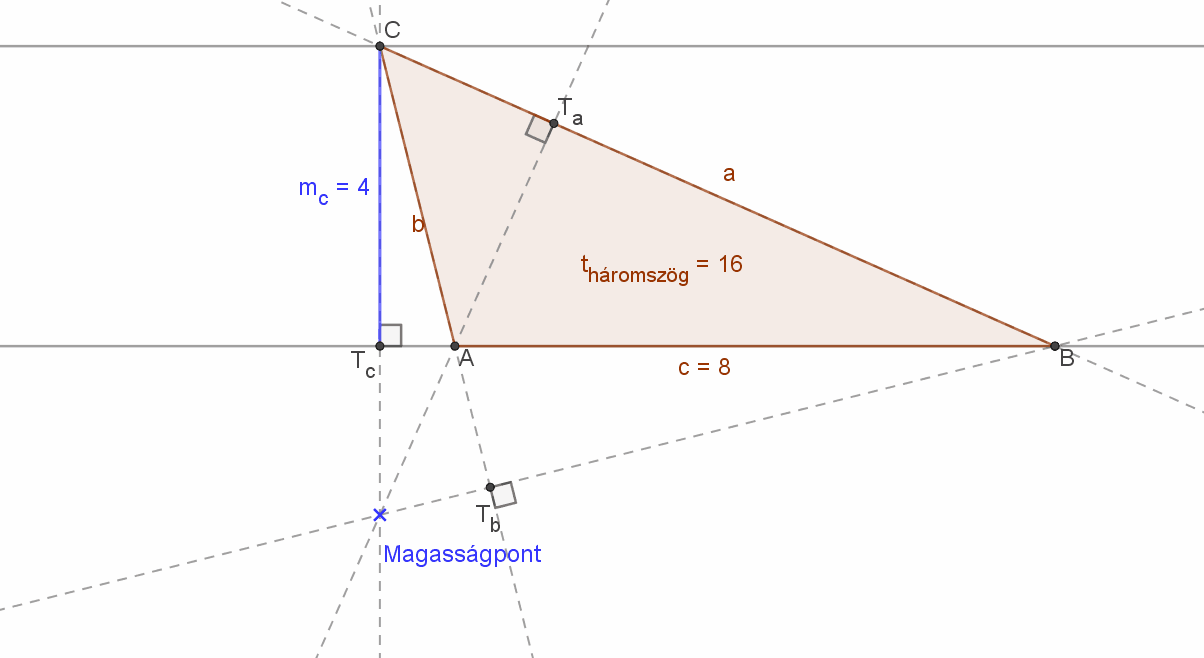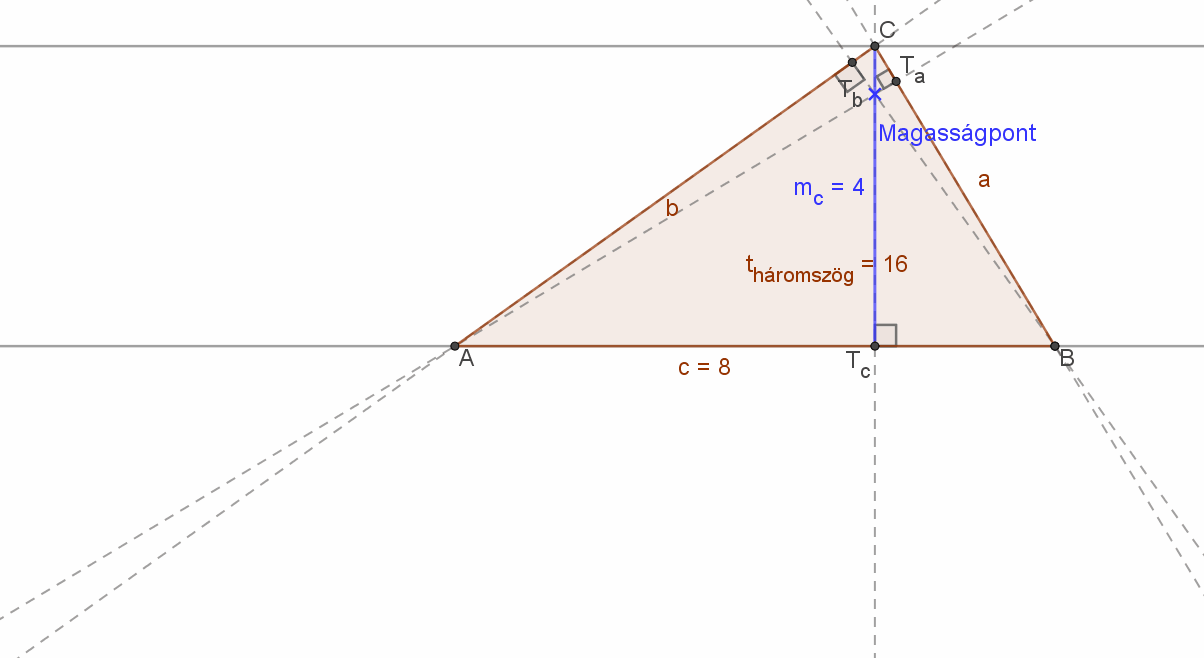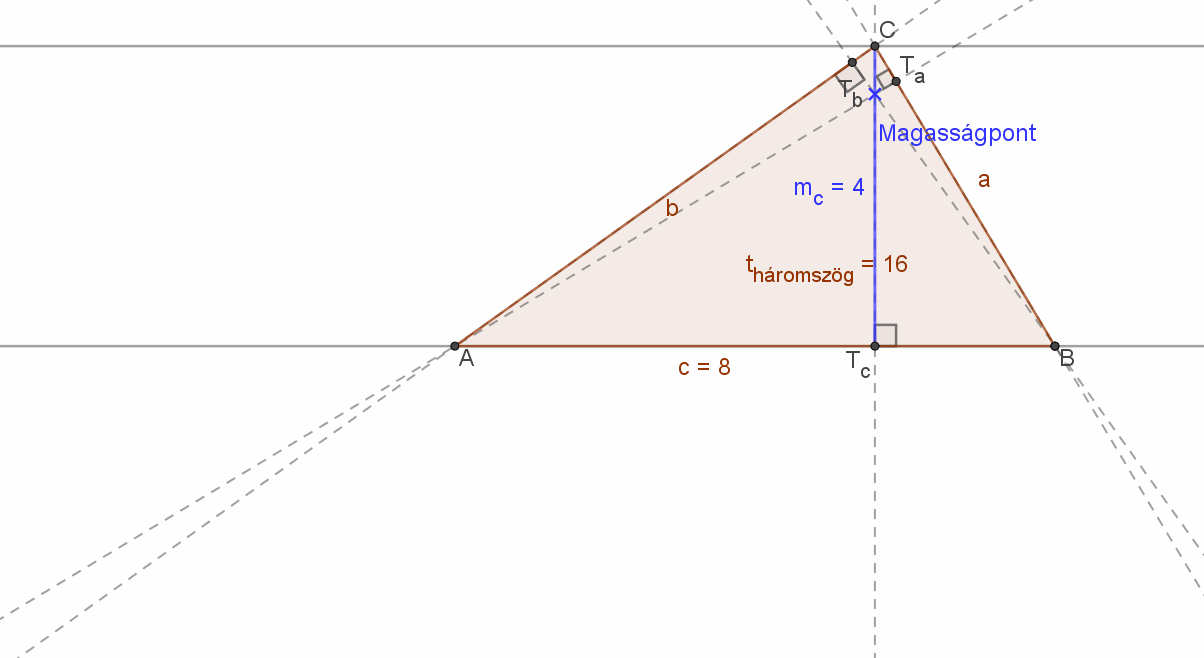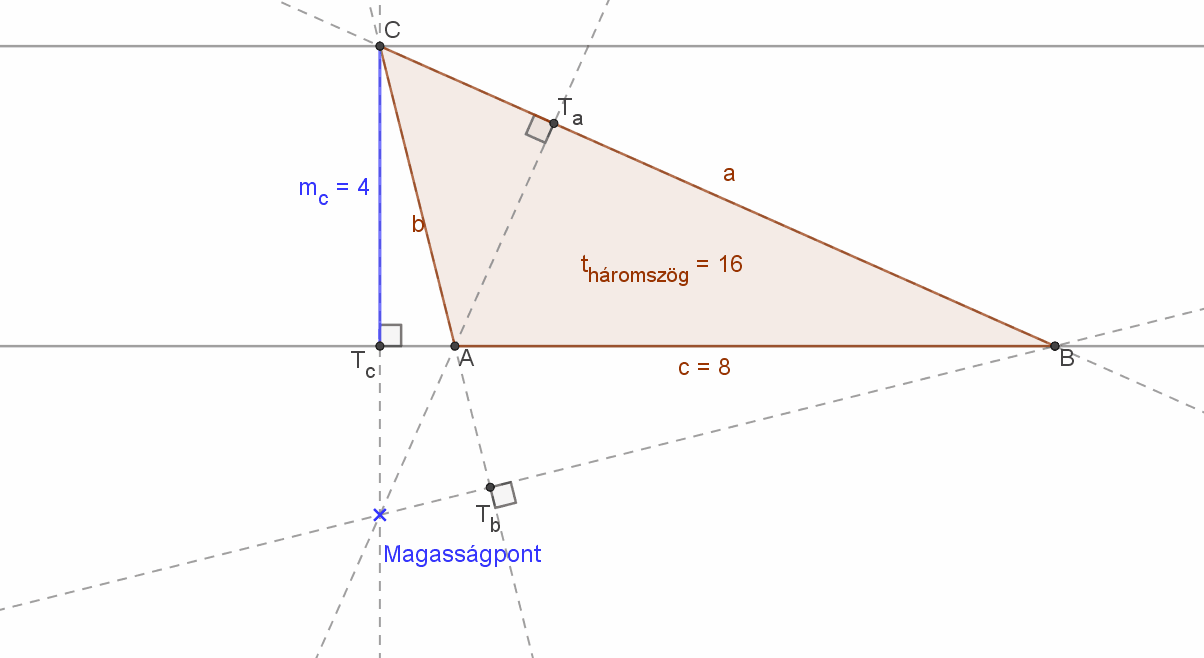
Ebben az animációban a háromszög „C” csúcsa a háromszög BC=a oldallal párhuzamosan mozog. A kapott háromszögek bár nem egybevágók, de a területeik egyenlők, hiszen az AB=c oldal hossza (8) és a C csúcshoz tartozó magasság (szakasz) hossza (mc=4) nem változik. Ezért a háromszög területe állandó, azaz tháromszög=16 területegység.


Comments are closed, but trackbacks and pingbacks are open.