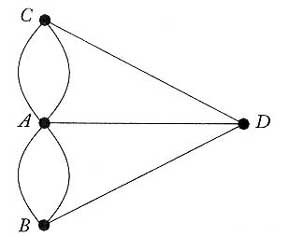
 Euler az 1736-ban szembesült a „königsbergi séta” problémájával, és bebizonyította, hogy ilyen útvonal nem lehetséges.
Euler az 1736-ban szembesült a „königsbergi séta” problémájával, és bebizonyította, hogy ilyen útvonal nem lehetséges.
Ő evvel az egyszerűsített modellel dolgozott. Ez egyben a gráfelmélet kezdete is, bár csak a XIX. század végén kezdődött meg ennek az új matematika szakterületnek a fejlődése. Egy gráf egy pontjába összefutó éleinek számát a pont fokszámának nevezzük.
A königsbergi gráfban az A csúcs fokszáma = 5, a B, C és D csúcsé pedig = 3.
Miért nem sikerülhet a a „königsbergi séta”? A probléma az egyes csúcsok fokszámában rejlik. Mivel egy hídon csak egyszer mehetek át, minden pontot érintenem kell és vissza kell jutni a kiindulási pontra, ezért szükséges, hogy minden pont a fokszáma páros legyen. (Ahová egyszer bementem, onnan ki is kell menni.)
A következő feladat közismert:
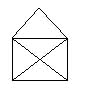 Rajzold le egyetlen ceruzavonással, a ceruza felemelése nélkül a mellékelt borítékot.
Rajzold le egyetlen ceruzavonással, a ceruza felemelése nélkül a mellékelt borítékot.
(Már megrajzolt vonalat keresztezhetünk, de rajta nem mehetünk.)
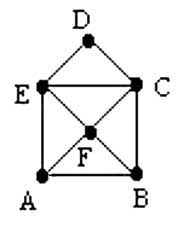 Megoldás:
Megoldás:
Rajzoljuk le gráfként és határozzuk meg csúcsainak fokszámát és az élek számát!
A, és B csúcs fokszáma 3.
C, E és F csúcsok fokszáma 4.
D csúcs fokszáma 2.
Fokszámok összege ebben a gráfban 20.
Élek száma pedig 10.
A felemelés nélküli rajzolás lehetséges. Egy lehetséges bejárás: A, E, C, F, A, B, F, E, D, C, B.
Mivel azonban a gráfban páratlan fokszámú csúcsok is vannak, nem lehetséges a kezdőpontba visszajutni.
A fenti problémák a gráfok bejárásával függenek össze. Ennek érdekében a következő fogalmakat érdemes megfogalmazni.
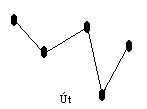 Útnak nevezzük a gráf egymáshoz csatlakozó éleinek olyan sorozatát, amely egyetlen ponton sem megy át egynél többször.
Útnak nevezzük a gráf egymáshoz csatlakozó éleinek olyan sorozatát, amely egyetlen ponton sem megy át egynél többször.
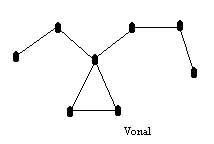 Vonalnak nevezzük a gráf csúcsainak és éleinek azt a sorát, amelyben az élek a megfelelő csúcsokat kötik össze és az élek nem ismétlődnek.
Vonalnak nevezzük a gráf csúcsainak és éleinek azt a sorát, amelyben az élek a megfelelő csúcsokat kötik össze és az élek nem ismétlődnek.
Euler-vonalnak az olyan vonalat nevezzük, amelyben a gráf minden éle és minden pontja szerepel. Az Euler-vonal mentén megrajzolhatjuk a gráfot úgy, hogy a ceruzánkat nem emeljük fel a papírról, minden élén pontosan egyszer haladunk végig.
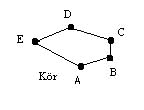 Körnek nevezzük a gráf egy kiindulási pontjába visszavezető utat, azaz olyan élsorozatot, amely a kiindulási pontjába tér vissza és benne minden él csak egyszer szerepel.
Körnek nevezzük a gráf egy kiindulási pontjába visszavezető utat, azaz olyan élsorozatot, amely a kiindulási pontjába tér vissza és benne minden él csak egyszer szerepel.
Ha egy Euler-vonal kör, akkor zárt Euler-vonalról beszélünk.
Tételek:
1. Egy összefüggő gráfnak akkor és csak akkor van zárt Euler-vonala, ha a gráf minden pontjának a fokszáma páros.
2. Ha az összefüggő gráfban csak két páratlan fokszámú csúcs van, akkor a gráfnak van nyitott Euler-vonala.
Tehát:
1. A „könisbergi séta” tehát olyan gráf, amelyben nincs Euler-vonal. Csak akkor lehet egy gráfban ilyen bejárást megvalósítani, ha minden csúcs fokszáma páros, azaz amelynek zárt Euler vonala van.
2. A borítékos feladatban a bejárás nyílt Euler vonal. Ez a”borítékos” feladat akkor oldható meg, ha páratlan fokszámú csúcsból indulunk és a másik páratlan fokszámú csúcsba érkezünk. De nem zárt Euler vonal, mert nem lehetséges kezdőpontba visszajutni, hiszen nem minden fokszám páros.


Comments are closed, but trackbacks and pingbacks are open.