A másodfokú egyenlet diszkriminánsa

A másodfokú egyenlet megoldóképletében a négyzetgyök alatt szereplő ​\( b^{2}-4ac \)​ kéttagú kifejezést a másodfokú egyenlet diszkriminánsának nevezzük. (gyakran D-vel jelöljük.)

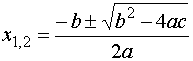
Itt az a, b, c betűk az ​\( ax^{2}+bx+c=0 \)​ másodfokú egyenlet általános alakjában szereplő együtthatók. (a≠0).

Ettől a ​\( D=b^{2}-4ac \)​ kéttagú kifejezéstől függ a másodfokú egyenlet megoldásainak száma a valós számok között.

1.      Ha a D=b²-4ac>0, akkor a másodfokú egyenletnek két különböző valós gyöke van, és ezeket a  fenti megoldóképlet segítségével határozhatjuk meg.

2. Ha D=b²-4ac=0, ekkor a másodfokú egyenletnek két egyenlő (kétszeres) gyöke van. Ezek: x₁=x₂=​\( -\frac{b}{2a} \).​ (Szokás helytelenül egy valós gyöknek is mondani.)

3. Ha D=b²-4ac<0 esetben a másodfokú egyenletnek nincs megoldása a valós számok között.

Diszkrimináns szó jelentése: meghatározó, döntő tényező.

Feladat:

A p paraméter mely valós értékeire van az (1-p⋅)x²-4p⋅x+4⋅(1-p)=0 egyenletnek legfeljebb egy valós gyöke. (Helyesebben: legfeljebb 2 egybeeső gyöke.)

(Összefoglaló feladatgyűjtemény 765. feladat.)

Megoldás:

1. Ha a p=1, akkor az adott egyenlet elsőfokú, és ennek gyöke x₁=0.

2. Ha a p paraméter 1-től különböző valós szám, akkor az adott egyenlet másodfokú, ennek megoldásainak száma a diszkriminánstól függ.

A feladat azt kívánja meg, hogy a diszkrimináns kisebb vagy egyenlő legyen nullánál, azaz b²-4ac≤0.
Itt a szereposztás: a=1-p; b=-4p; c=4⋅(1-p).
A diszkrimináns így D=(-4p)²-4(1-p)4(1-p). Ennek kell kisebb vagy egyenlőnek lennie nullánál.
Tehát a 16p²-16(1-p)²≤0 egyenlőtlenséget kell megoldani.
Ez az egyenlőtlenség a 16p²-16(1-2p+p²)≤0 alakba írható amelyet tovább alakítva -16+32p≤0. Azaz p≤0,5.

p=0,5 esetben kétszeres gyöke, azaz két egyenlő gyöke van az
(1-0,5)⋅x²-4⋅0,5x-4⋅(1-0,5)=0, azaz 0,5x²-2x-2=0 egyenletnek, azaz x₁=x₂=-2.

p<0,5 esetben a diszkrimináns negatív, tehát az (1-p)⋅x²-4p⋅x+4⋅(1-p)=0 egyenletnek nincs valós gyöke.