Függvénytranszformációk

A  középiskolai tananyagban előforduló legfontosabb függvénytranszformációk.

1. A függvények értékére vonatkozó transzformációk

1.1 Függvény szorzása egy pozitív állandóval.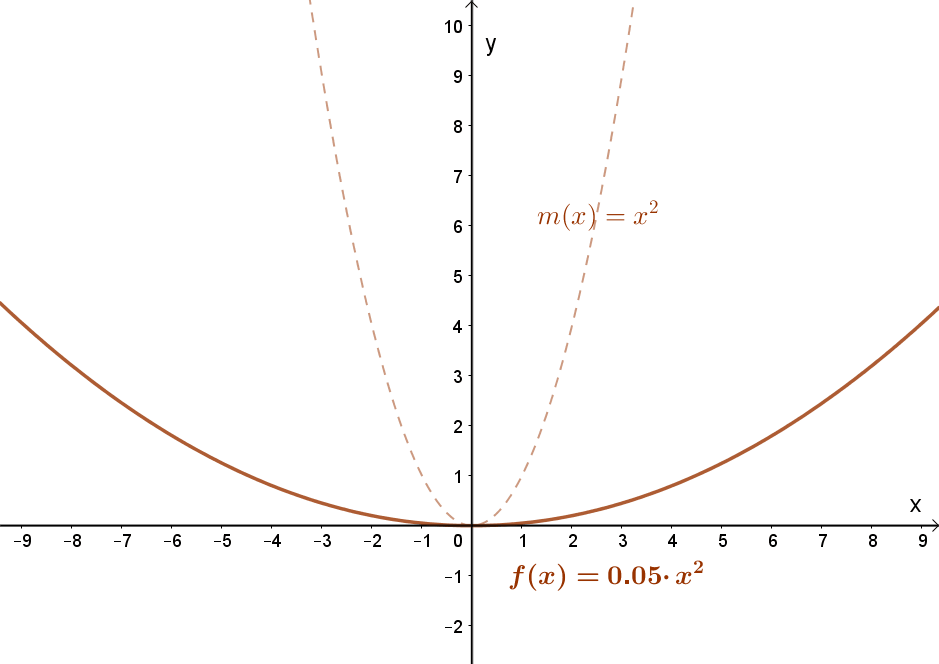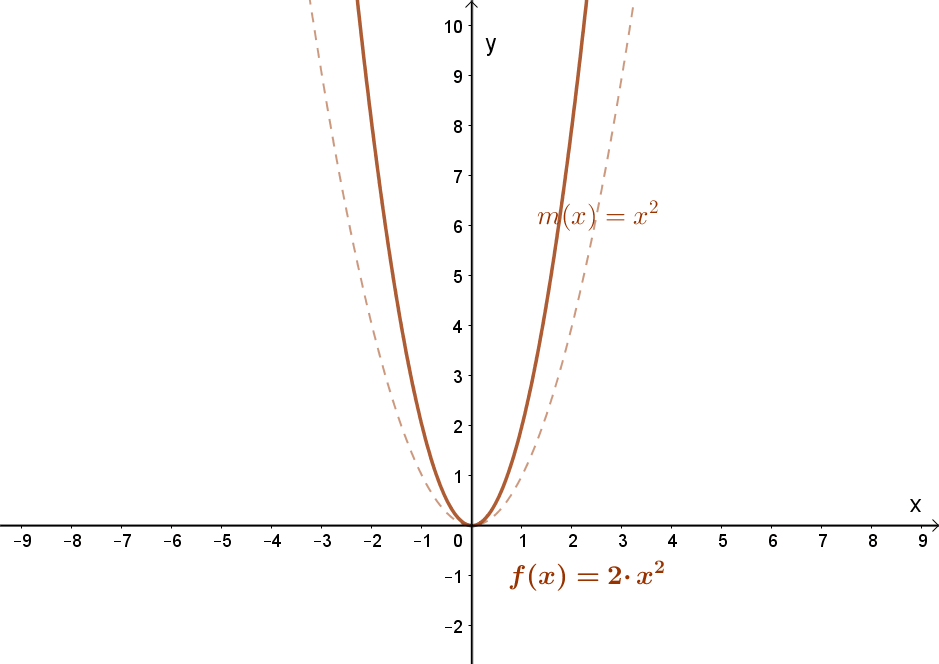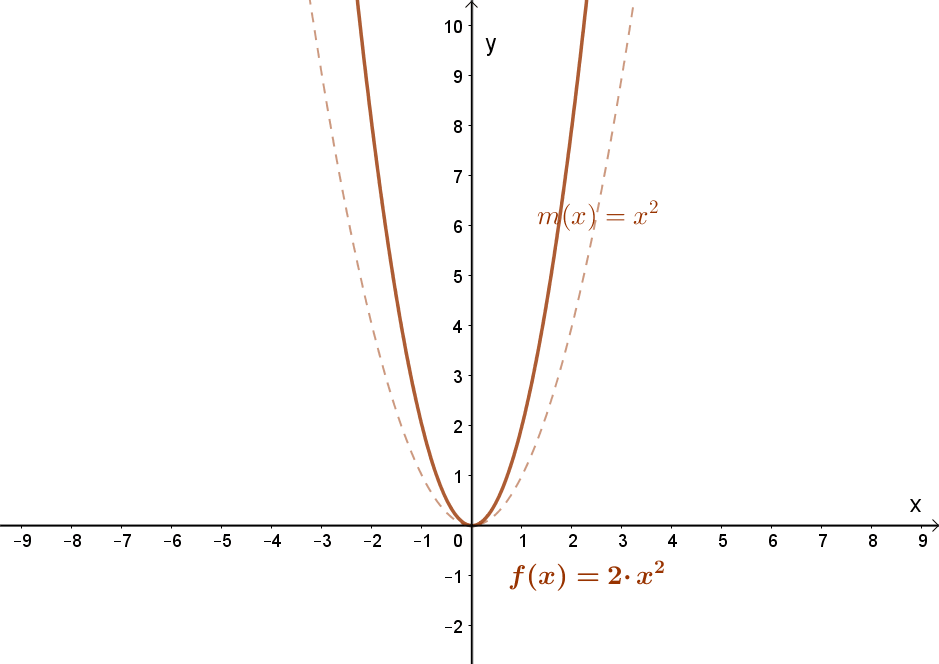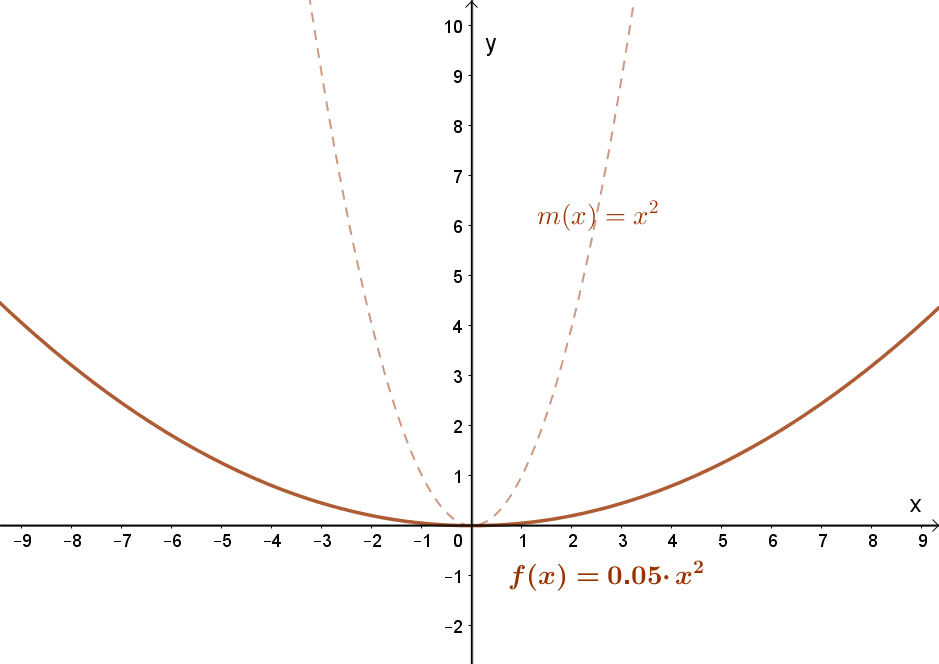

Jelölés:c⋅f(x); c>0. A függvény meredekségének változása.
„Nyújtás” az „y” tengely mentén. Nyújtás, ha „c”> 1 és összenyomás, ha 0<c<1. Lásd a fenti animációt! 

1.2 Függvény szorzása -1-gyel.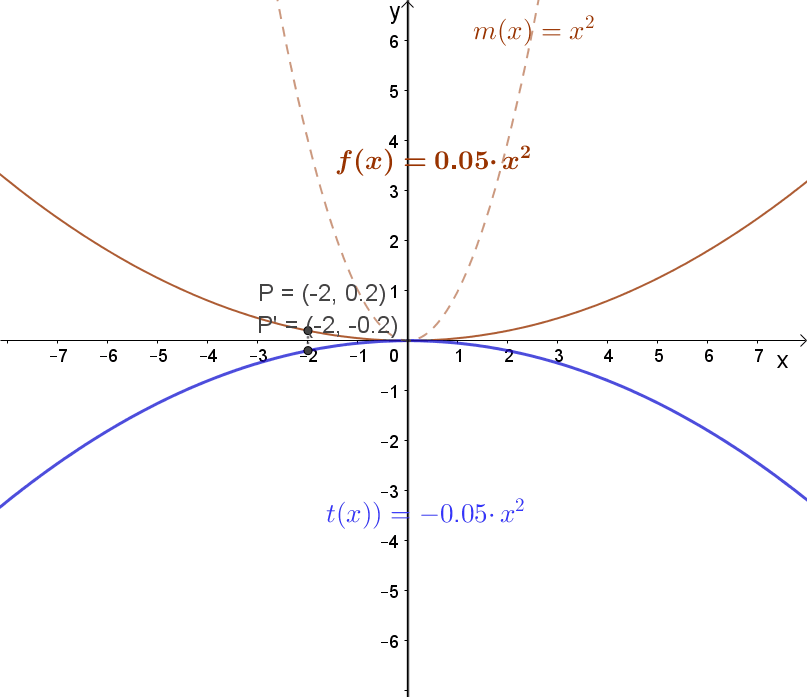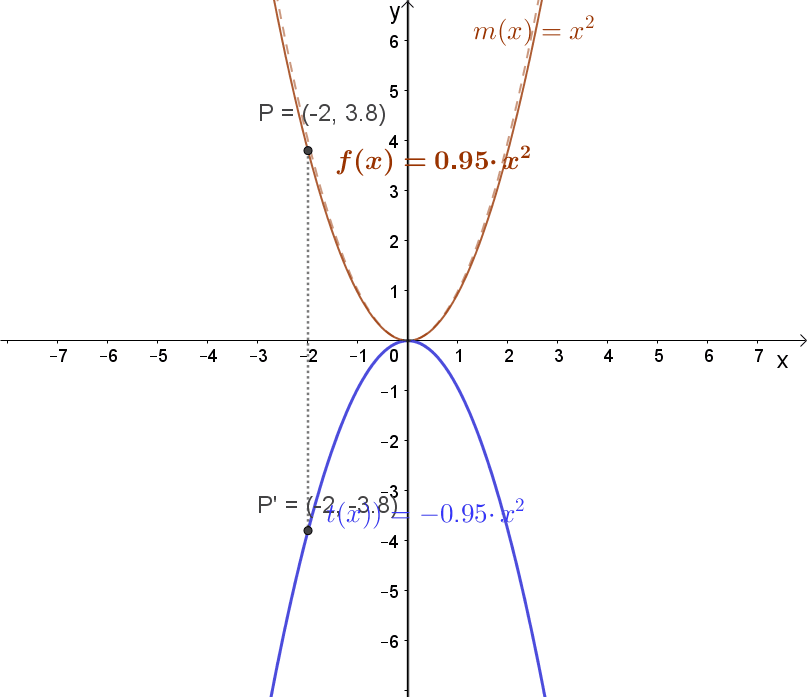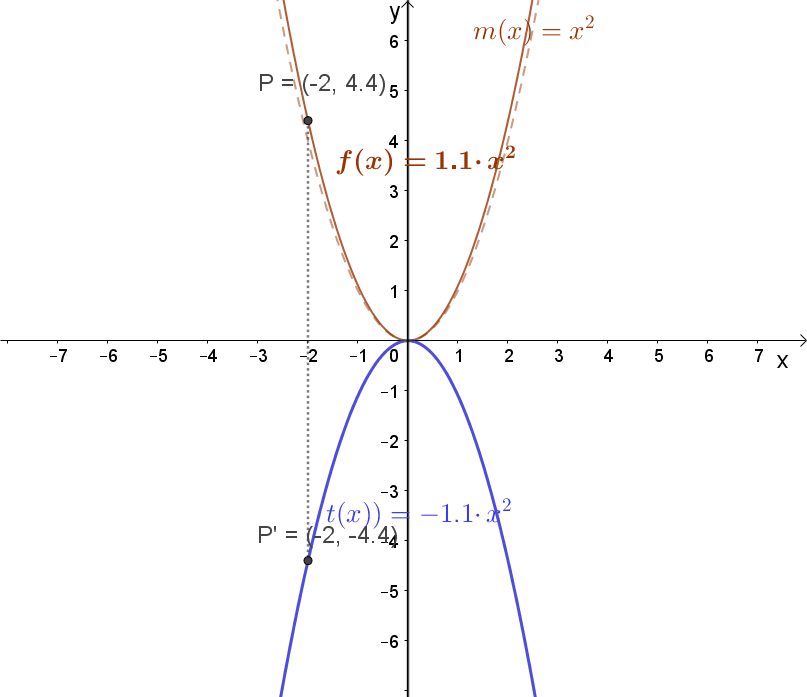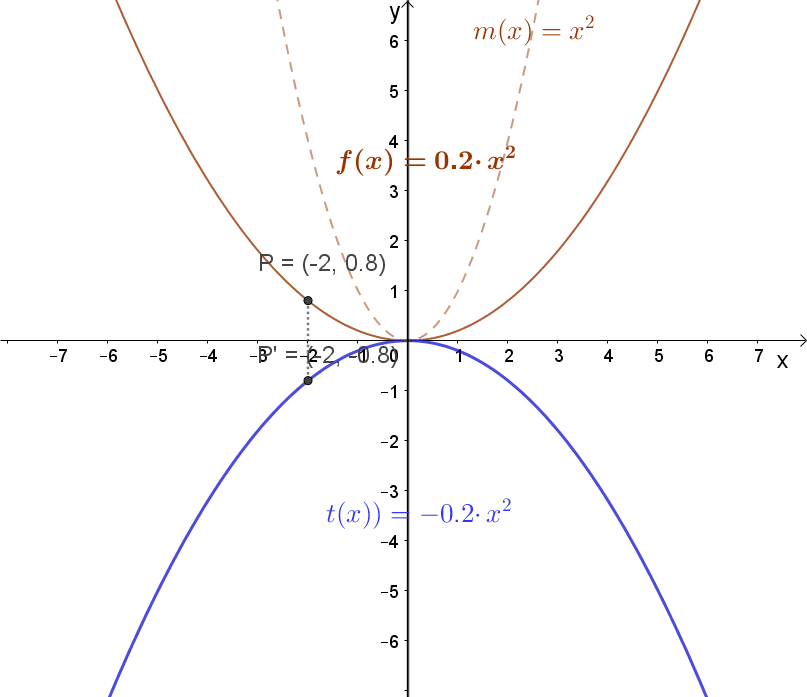

Jelölés: -1⋅m(x). A függvény tükrözése az „x” tengelyre. Lásd a fenti animációt! 

1.3 Egy állandó hozzáadása a függvény értékéhez.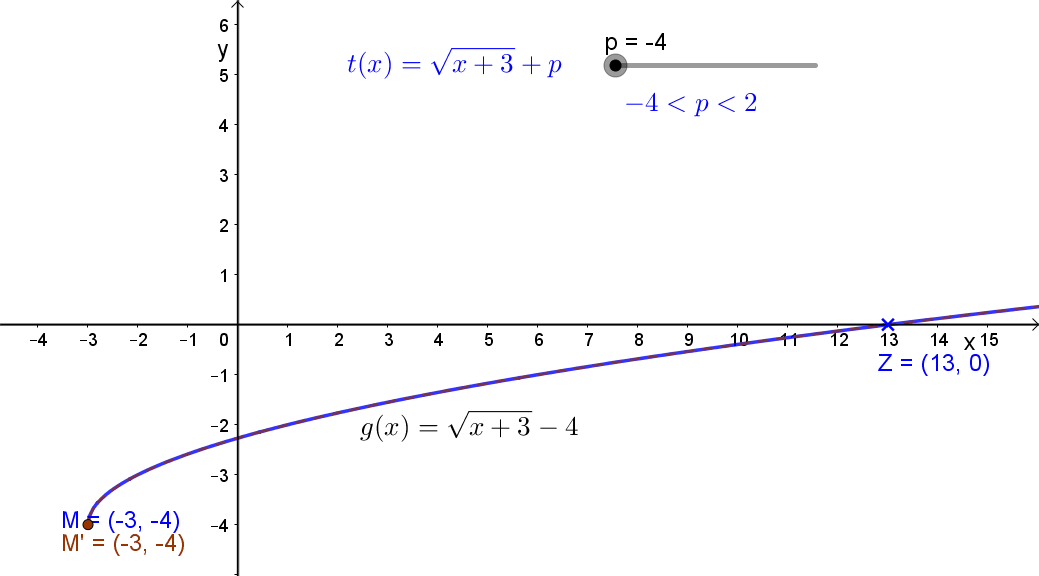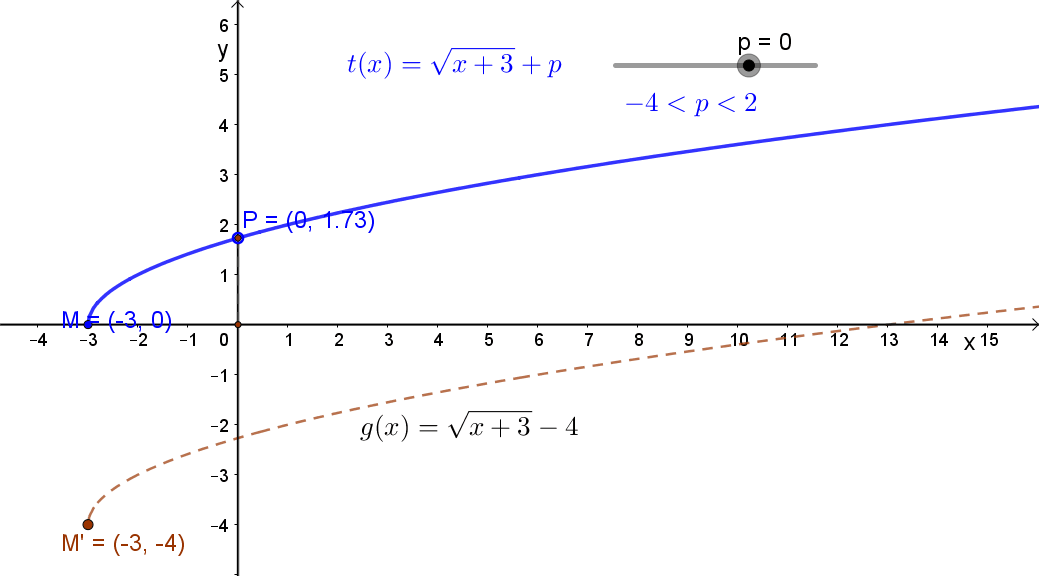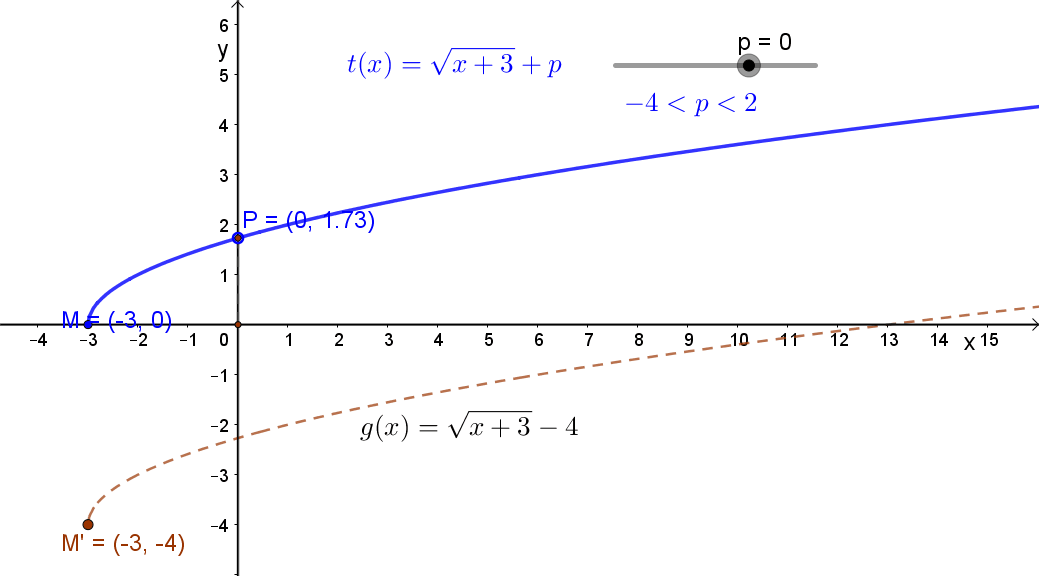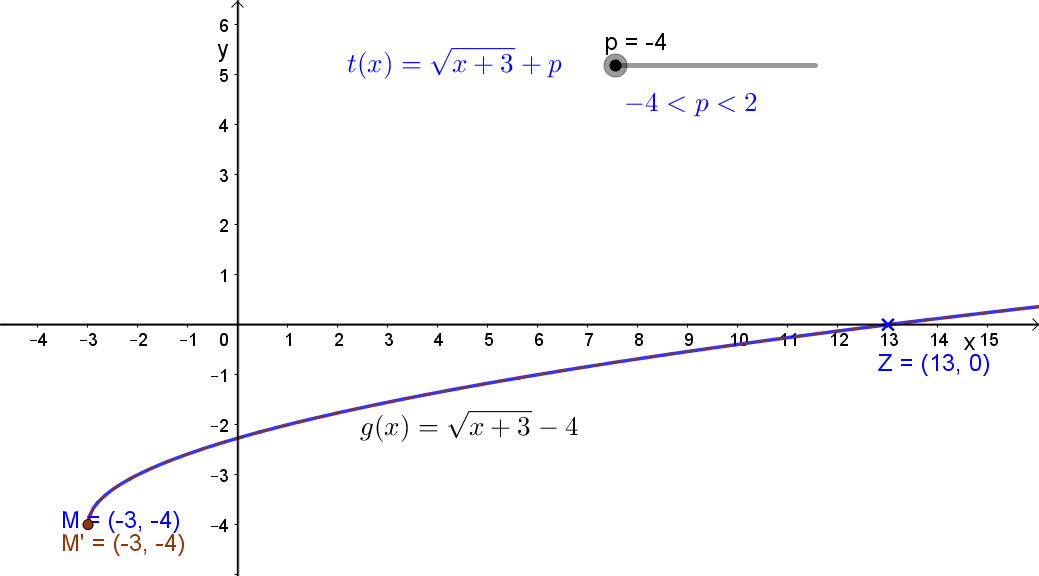 Jelölés: g(x)+c. A függvény eltolása az „y” tengely mentén.
Ha c>0, akkor pozitív irányban,ha c<0, akkor negatív irányban. Lásd a fenti animációt! 

 

1.4 Függvény abszolút értéke.

 

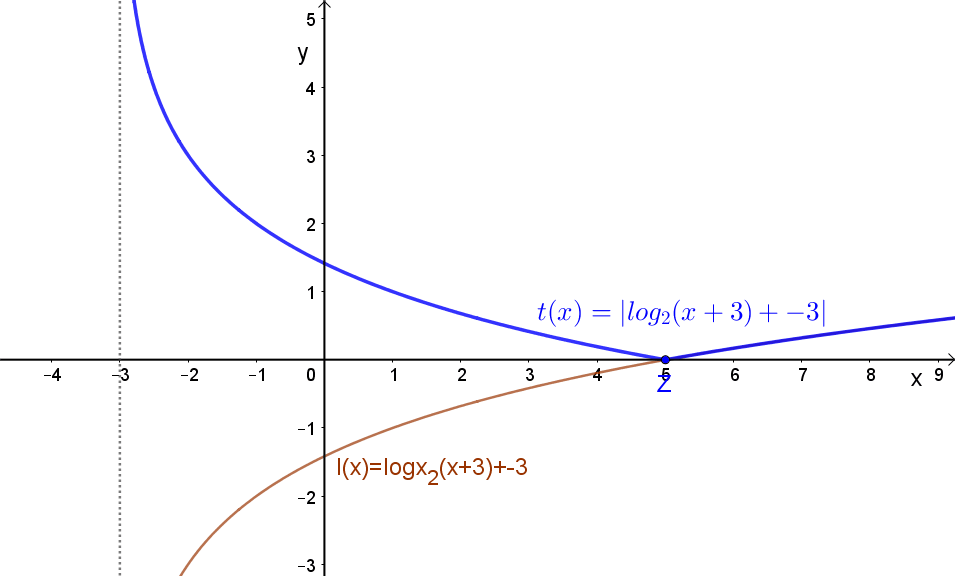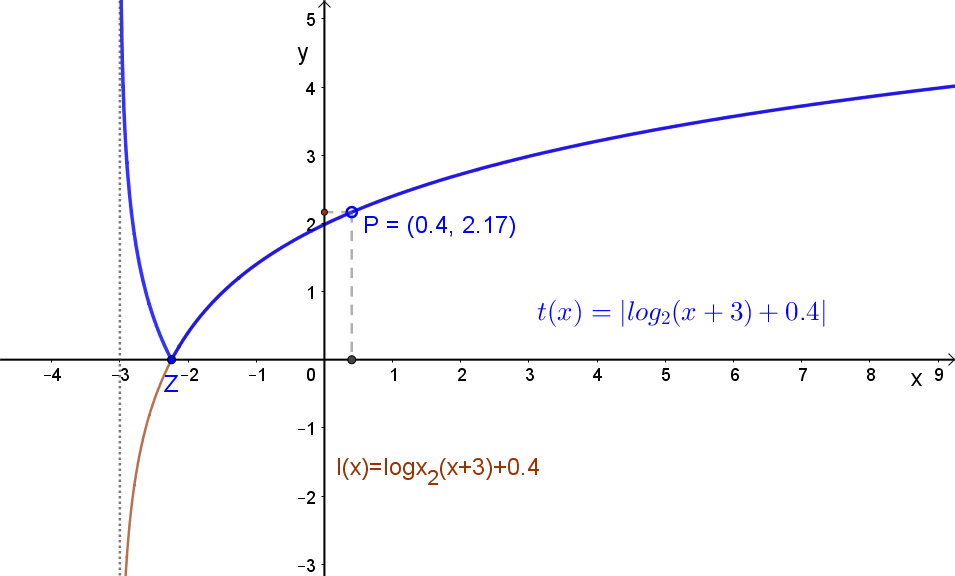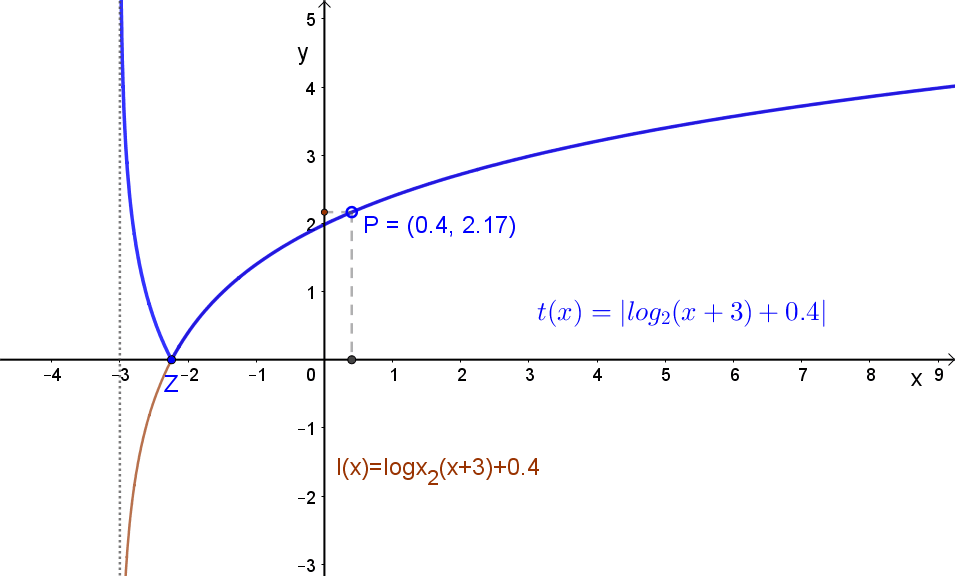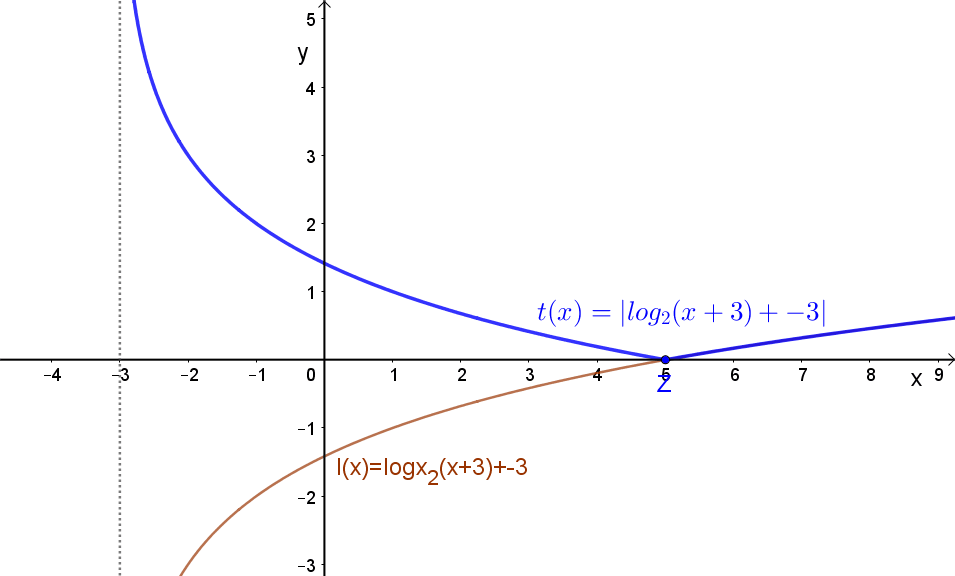
Jelölés: |f(x)|​.

A függvény negatív részének tükrözése az „x” tengelyre.

Például: ​​\( t(x)=\left|log_{2}\left(x+3)+p \right) \right| \)​.

 

2. A függvény váltózójára vonatkozó transzformációk

2.1 Egy állandó hozzáadása függvény változójához.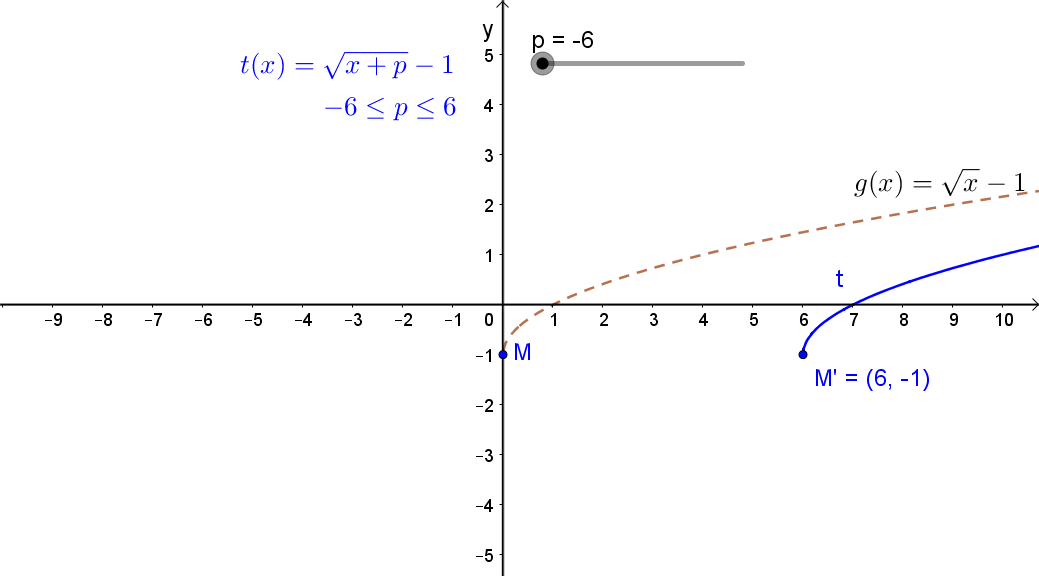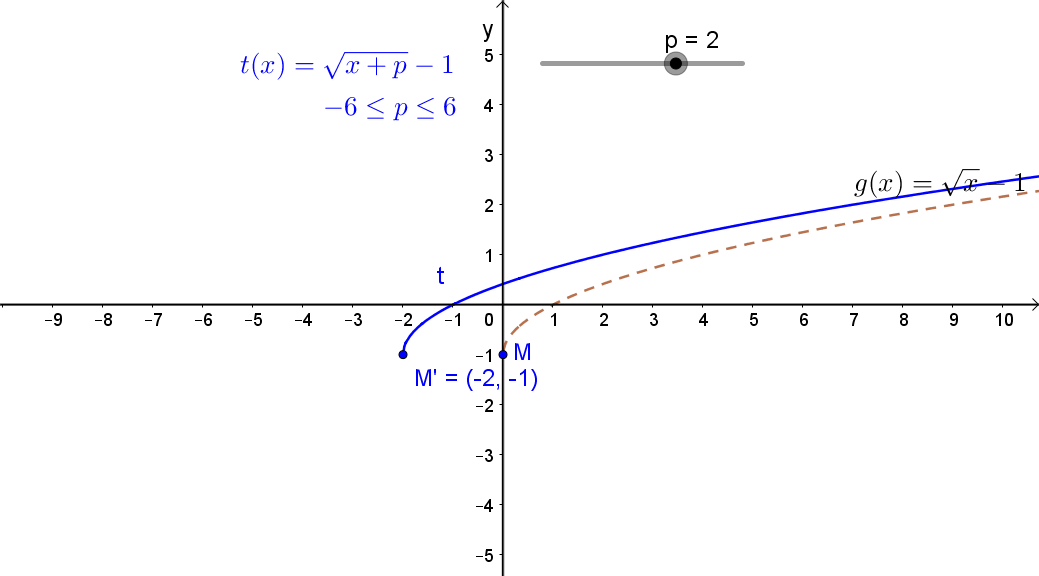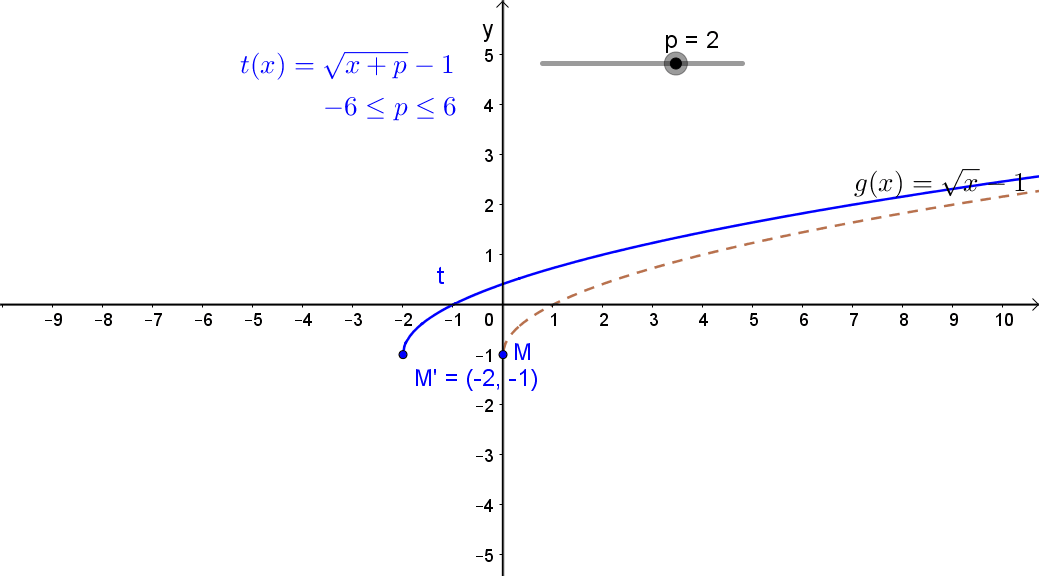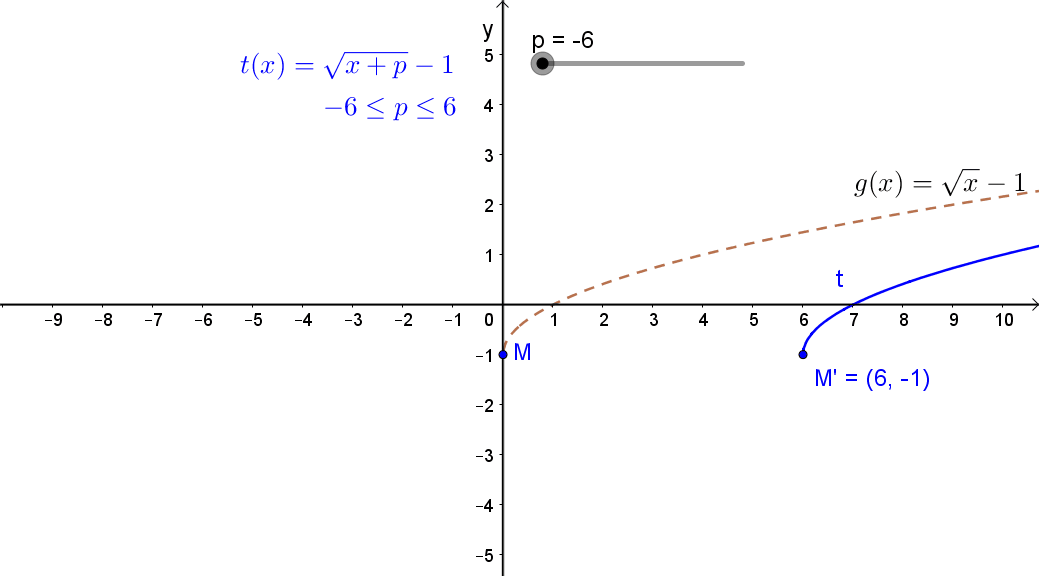 

Jelölés: g(x+c).

A függvény eltolása az „x” tengely mentén.
Ha c>0, akkor negatív irányban,ha c<0, akkor pozitív irányban.

Például:  ​\( g(x)=\sqrt{x-2} \)​

 

 

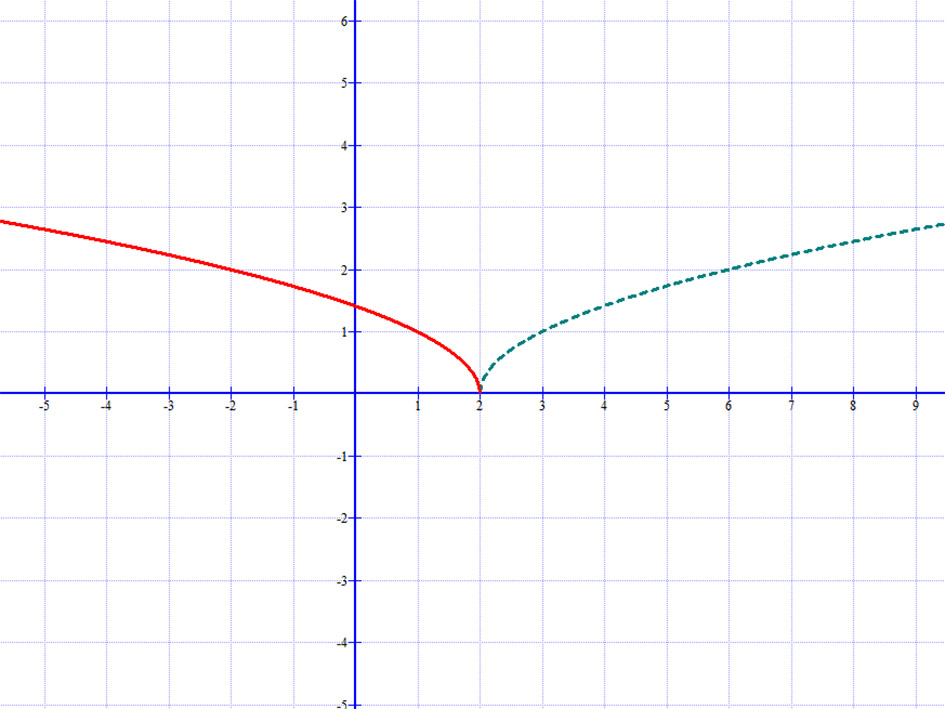2.2 Függvény változójának szorzása c=-1-gyel.

Jelölés: g(-1⋅x).

Tükrözés az x tengely mentén.

Például: ​\( g(x)=\sqrt{-1·(x-2)} \).

 

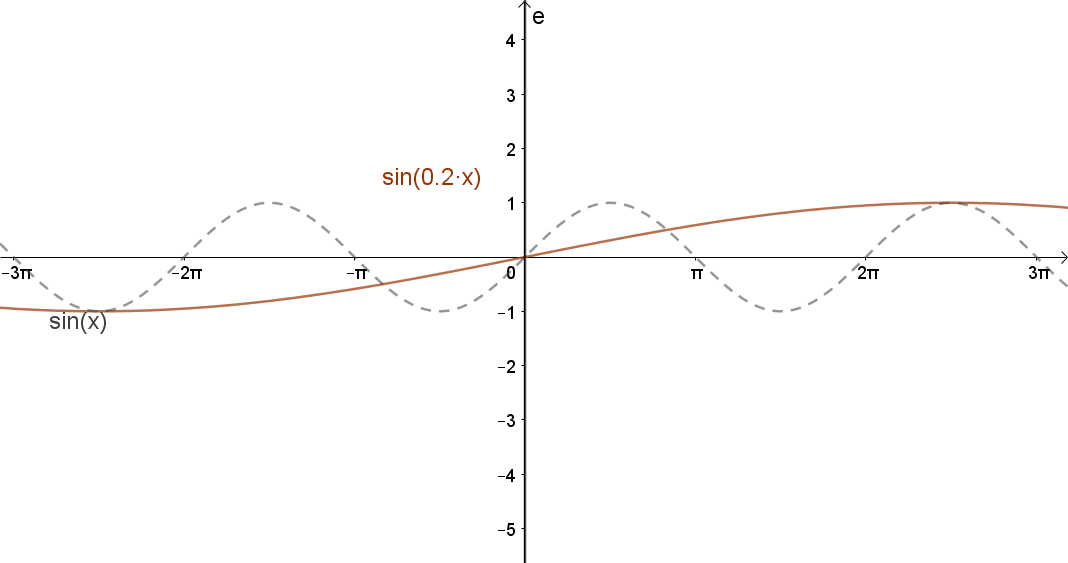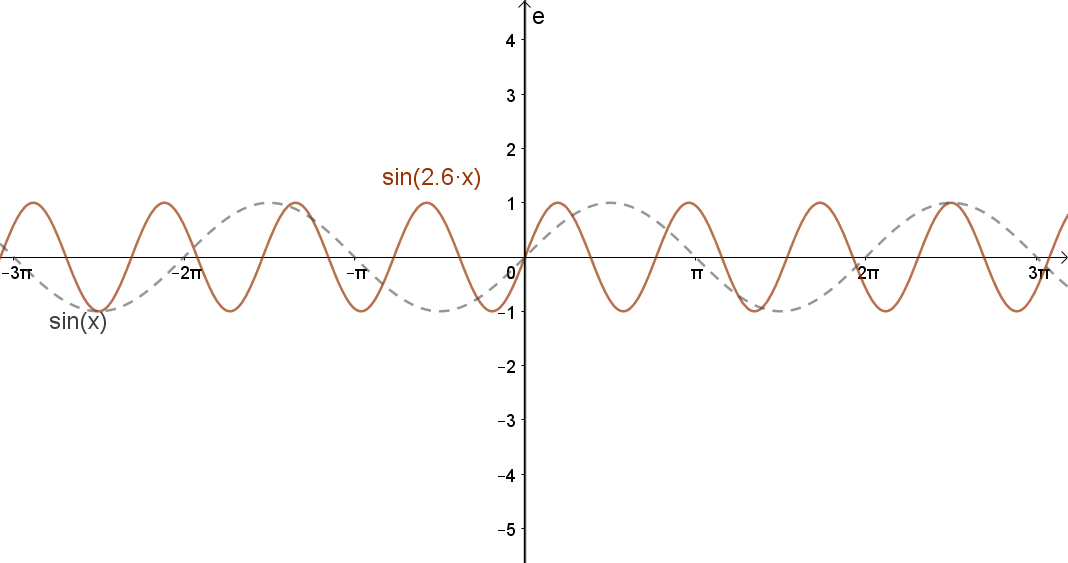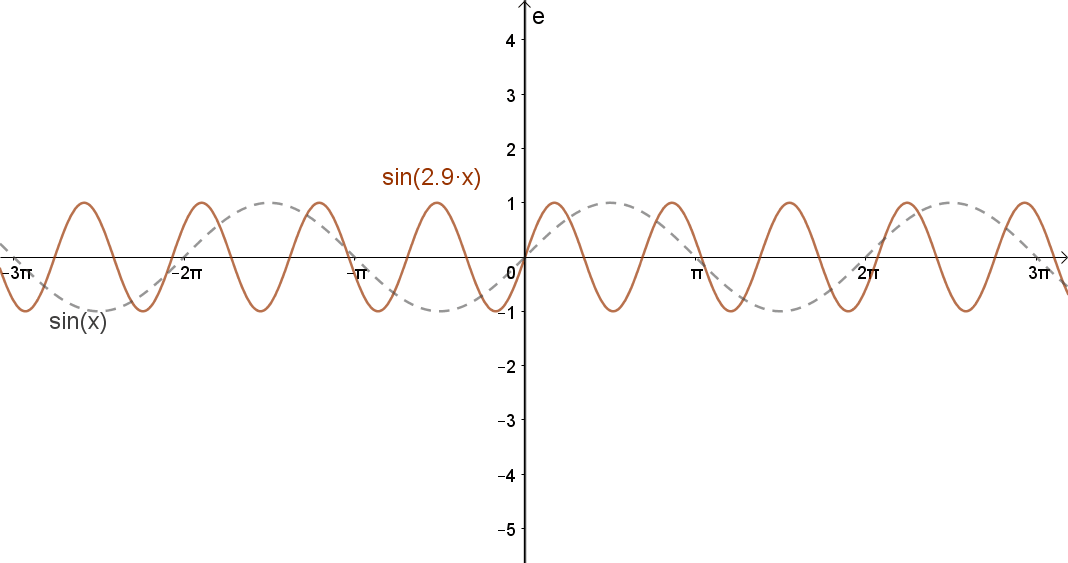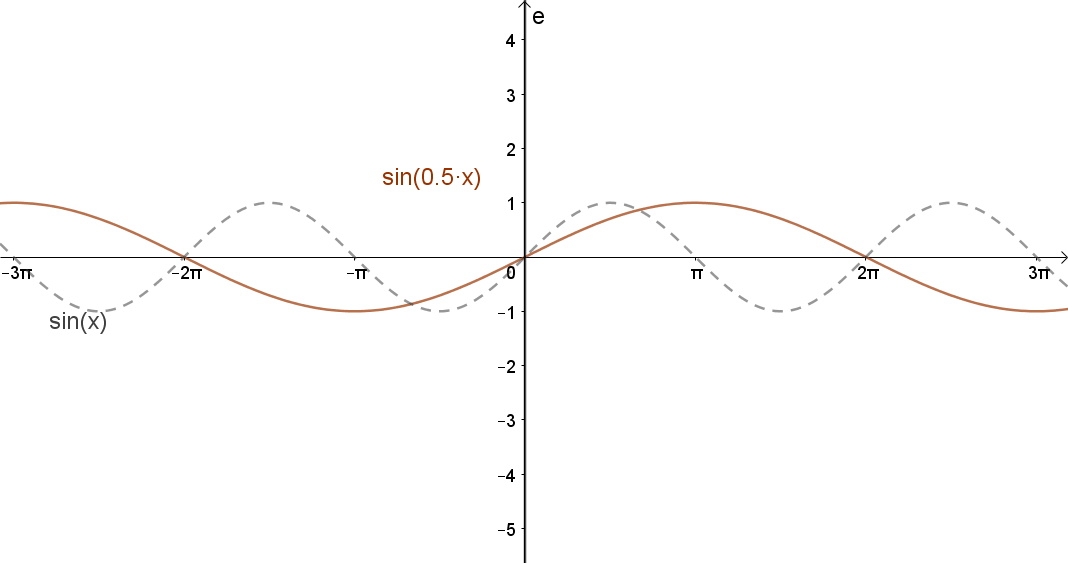2.3 Függvény változójának szorzása egy pozitív állandóval.

Jelölés: m(c⋅x); c>0.

„Nyújtás” az x tengely mentén.
Ha c>1, összehúzás, ha c<1, akkor nyújtás.

Például: sin(c⋅x).

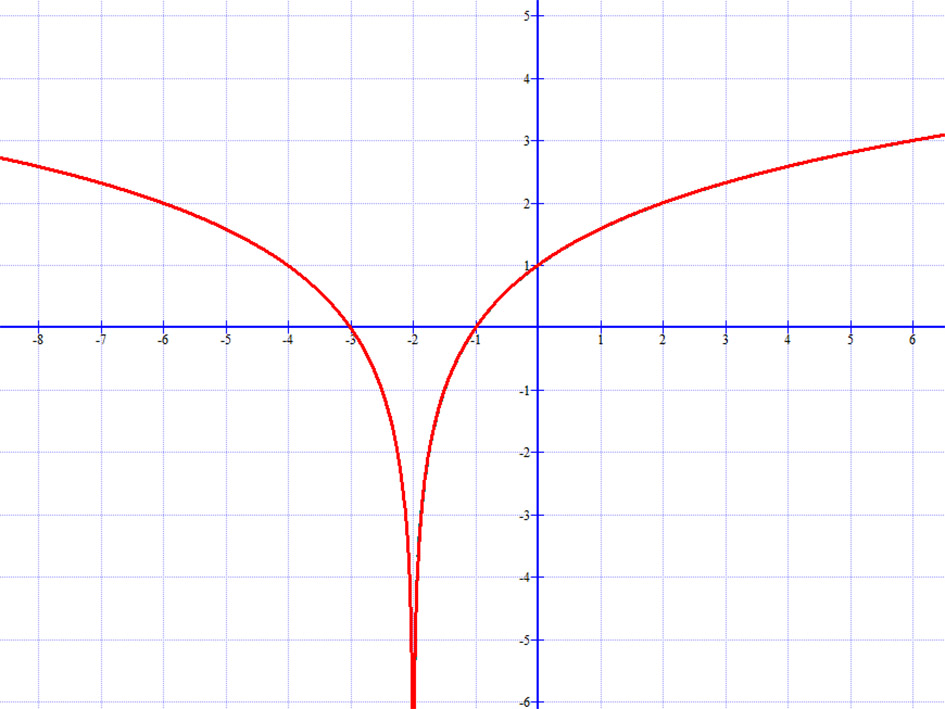
2.4 Függvény változójának abszolút értéke.

Jelölés: f|x|.

A függvény tükrözése az y tengellyel párhuzamos tengelyre.

Például: ​\( l(x)=log_{2}\left|x+2\right| \)​