Fokszám tétel

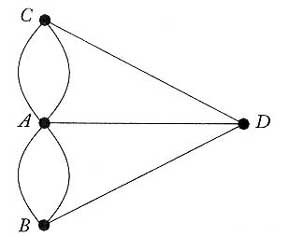
Nézzük az un. „königsbergi gráfot”

Ebben a gráfban 7 él van. Az „A” pontból 5 él, a „B”, a „C”  pontból és a „D” pontokból is 3-3 él indul ki.

Definíció:

A gráf egy pontjába összefutó élek számát a pont fokszámának nevezzük.

A fenti gráfban tehát „A”fokszáma=5 míg „B”=”C”=D” pontok fokszáma: 3.
A fokszámok összege: 14, ami az élek számának a kétszerese.

Ez persze nem véletlen, hiszen minden élet kétszer, a kezdő és a végpontnál is figyelembe vettük a fokszámok összegénél.

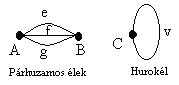Az itt mellékelt, párhuzamos éleket tartalmazó gráfban két csúcs (pont) és három él van. Az „A” és „B” csúcsok fokszáma 3. Így a fokszámok összege 6.  A másik, hurokélt tartalmazó kis gráfban mindössze egy pont van. De ennek a pontnak a fokszáma 2, mert a kezdőpont és a végpont itt egybeesik.

Tételek:

1. Egy gráfban a fokszámok összege az élek számának a kétszerese.
Másképpen: bármely gráfban a fokszámok összege páros szám.
Hiszen a gráf minden élének két végpontja van. A hurokélt úgy tekintjük, hogy kétszeresen illeszkedik a pontra.

2. Egy gráfban a páratlan fokszámú pontok száma páros.
Csak így lehet a fokszámok összege páratlan számú él esetén páros szám.

3. A teljes gráfban a fokszámok összege: n⋅(n-1).

4. A teljes gráfban az élek száma: ​\( \frac{n\left(n-1 \right) }{2}=\binom{n}{2} \)​

Feladat:

Egy hét tagú társaságban (kölcsönös) barátságok vannak. Az egyes tagoknak következők a barátai: Andrásnak 3, Bélának 2, Csabának 5, Daninak 1, Ervinnek 4, Ferinek 5 barátja van.  Hány barátja lehet Gábornak?

(Az Egységes Feladatgyűjtemény 230. feladata mentén.)

Megoldás:

Az egyes ember barátainak száma a gráf egyes pontjainak fokszáma.
Ezek összege: 3+2+5+1+4+5 =20
A fokszám tétel miatt Gábor barátainak száma csak páros szám lehet azaz 0, 2, 4 vagy 6.

1. eset: Gábor barátainak száma = 0. Ez nem lehetséges.
Akkor a többiek egy olyan hatpontú egyszerű gráfot alkotnak, ahol két olyan pont is van, amelyek fokszáma öt, azaz ezekből minden pontba megy él. Ez ellentmond annak, hogy Daninak csak egy barátja van. Ellentmondásra jutottunk. Az nem lehet, hogy Gábornak nincs barátja.

2. eset: Gábor barátainak száma = 6.  Ez sem lehetséges.
Mivel Dani fokszáma 1, ezért ebben az esetben csak Gábor ismerheti Danit. Ebből következik, hogy Danit sem Feri sem Csaba nem ismerheti.
Ekkor viszont Ferinek és Csabának is ismernie kellene Bélát, de mindketten nem ismerhetik, mert Béla ismerőseinek száma 2, és ezek közül az egyik Gábor lenne. Így tehát ebben az esetben is ellenmondásra jutottunk.

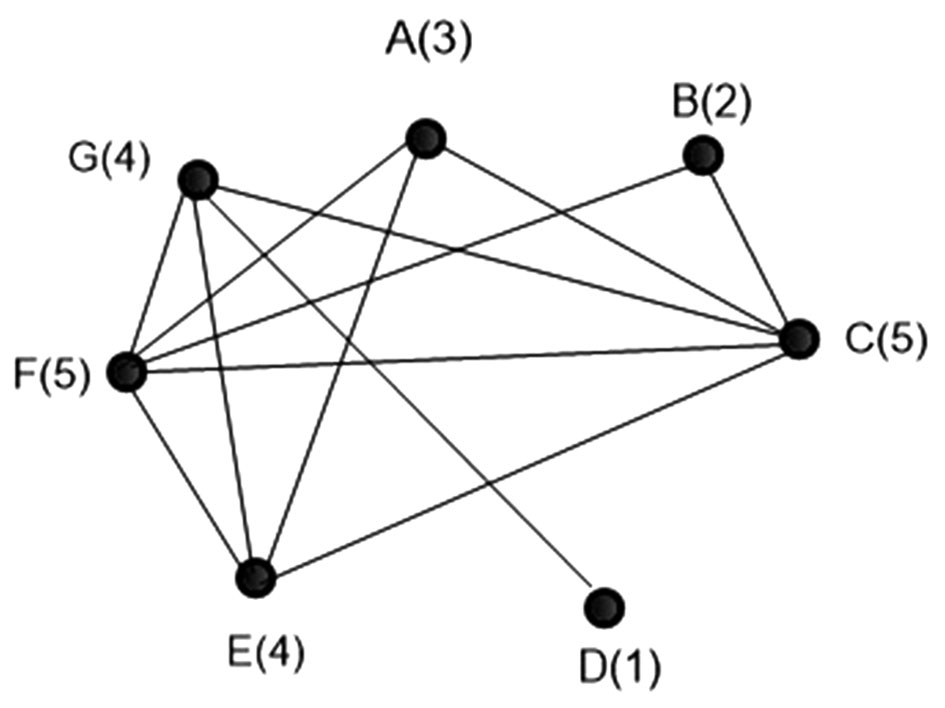3. eset: Gábor barátainak száma = 4. Igen, ez lehetséges.
Gábor barátai lehetnek: Csaba, Dani, Ervin és Feri.
Lásd a mellékelt ábrát!

De más jó megoldás is lehet.
Például Gábor barátai lehetnek: András, Csaba, Ervin és Feri.

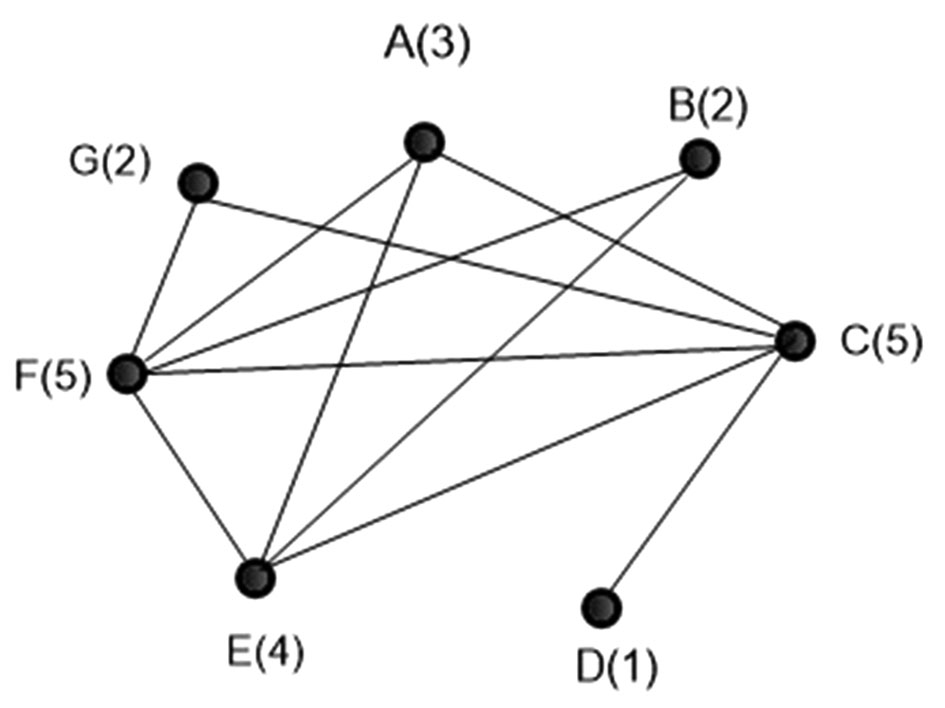
4. eset: Gábor barátainak száma = 2. Igen, ez az eset is lehetséges.
Gábor barátai lehetnek: Csaba és Feri.
Lásd a mellékelt ábrát!

 

Tehát az eredmény: Gábornak vagy 2 vagy 4 barátja lehet ebben a társaságban.

Nézzük a következő feladatot:

Előfordulhat-e, hogy egy 9 tagú társaságban mindenki pontosan 3 embert ismer?

Megoldás:

Készítsünk olyan gráfot, ahol a gráf csúcsai az egyes embereket (A, B,…I), élei pedig az ismeretséget jelentik. A feladat azt kívánja meg, hogy minden csúcsból pontosan három él induljon ki.

A mellékelt konkrét esetben:

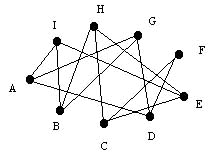A ismeri: D-t, G-t, és I-t, fokszáma: 3
B ismeri: G-t, H-t, és I-t, fokszáma: 3
C ismeri: E-t, F-t, és H-t, fokszáma: 3
D ismeri: A-t, F-t, és G-t, fokszáma: 3
E ismeri: C-t, H-t, és I-t, fokszáma: 3
F ismeri: C-t, D-t, fokszáma: 2
G ismeri: A-t, B-t, és D-t, fokszáma: 3
H ismeri: B-t, C-t, és E-t, fokszáma: 3
I ismeri: A-t, B-t, és E-t, fokszáma:3

A társaságban F csak 2 embert ismer.
Ebben a gráfban az élek száma: 13, a fokszámok összege:8*3+2=26

Ez nem jó megoldás, hiszen „F” csúcsból csak két él kapcsolódik, ugyanakkor a többi 8 csúcs fokszáma 3. Ha F bárki mást ismerne C-n és D-n kívül. akkor annak a pontnak a fokszáma már 4 lenne.

A feladat tehát nem oldható meg, hiszen ha a csúcsok száma 9, minden csúcs fokszáma 3, akkor a fokszámok összege 27 lenne.