Feltételes valószínűség

1. Feladat

Egy urnában 10 piros és 8 kék golyó van. Egymás után két golyót kihúzunk az urnából.
Mennyi a valószínűsége annak, hogy a másodiknak kihúzott golyó kék feltéve, hogy az elsőként kihúzott golyó piros?

NT-14311 203. oldal

Megoldás:

Legyen „B” esemény: {Az elsőnek húzott golyó piros.}

A ”B” esemény valószínűsége: \( P(B)=\frac{10}{18}≈0.56 \).

Legyen „A” esemény: {A másodiknak húzott golyó kék.}

Az „A” esemény kétféleképpen fordulhat elő attól függően, hogy elsőre mit húztunk.
Ennek valószínűsége tehát: \( P(A)=\frac{10}{18}·\frac{8}{17}+\frac{8}{18}·\frac{7}{17}=\frac{136}{306}≈0.44 \).

Az A⋅B esemény azt jelenti, hogy mind az A és mind a B esemény is bekövetkezett.
Ennek valószínűsége: \( P(A·B)=\frac{10}{18}·\frac{8}{17}=\frac{40}{153}≈0,26 \).

Sokszor hasznos lehet a folyamatot gráffal szemléltetni.
Készítsük el a folyamat fagráfját és írjuk oda az egyes lépések valószínűségeit!

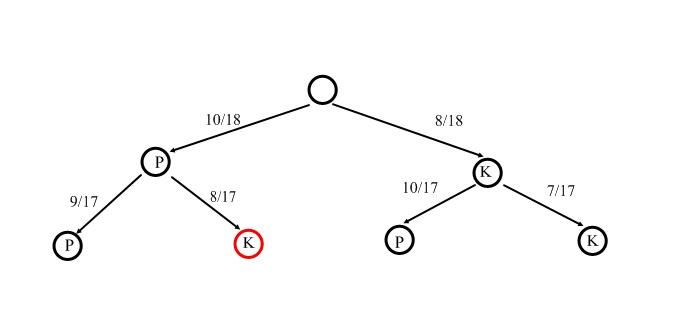
Képezzük a P(AB)/P(B) hányadost: \( \frac{P(A·B)}{P(B)}=\left(\frac{10}{18}·\frac{8}{17} \right):\frac{10}{18} ≈0.47 \).

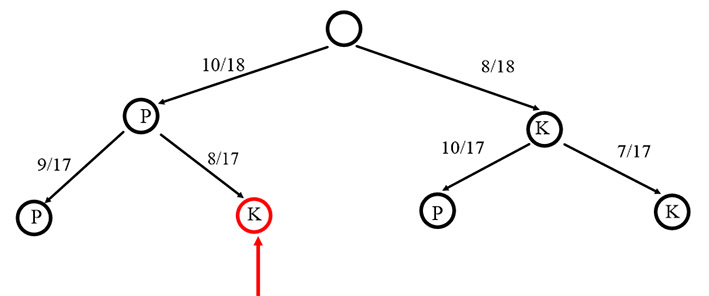
A \( \frac{P(A·B)}{P(B)} \) hányados annak a valószínűsége, hogy a másodiknak kihúzott golyó kék, feltéve, hogy az elsőként kihúzott golyó piros. Ezt a valószínűséget úgy fogalmazhatjuk meg, hogy ez az érték az „A” esemény bekövetkezésének az esélye feltéve, hogy a „B” esemény is bekövetkezik.

2. Feladat

Legyen az „A” esemény az, hogy két kockával dobott számok összege legfeljebb 8, „B” pedig az az esemény, hogy a dobott számok összege legalább 5. Számítsuk ki a \( \frac{P(A·B)}{P(B)} \) hányados értékét!

MX-350 176. old.

Megoldás:

Az „A” esemény 26 esetben következik be. ( (Megjegyzés: Az \( \overline{A} \) esemény: a dobott számok összege nagyobb mint 8. Ez 10 esetben fordul elő.) Mivel az összes esetek száma 36, ezért az „A” esemény valószínűsége: \( P(A)=\frac{26}{36}=\frac{13}{18}≈0,72. \)

A „B” esemény akkor következik be, ha a dobott számok összege 5, 6, 7, 8, 9, 10, 11 vagy 12.
Ez az esemény 30 esetben következik be. (Megjegyzés: A \( \overline{B} \) esemény: a dobott számok összege kisebb mint 5, ez 6 esetben fordul elő). Mivel az összes esetek száma 36, ezért a B esemény valószínűsége: \( P(B)=\frac{30}{36}=\frac{5}{6}≈0,83. \)

Az A⋅B esemény akkor következik be, h a dobott számok összege 5; 6; 7; 8.

Ez 20 esetben következik be. Mert:

Dobott számok összege 5: (1;4), (2;3), 4;1), (3;2). Tehát 4 ilyen eset van.
Dobott számok összege 6: (1;5), (2;4), (3;3), (4;2) és (4;1). Tehát 5 ilyen eset van.
Dobott számok összege 7: (1;6), (2;5), (3;4), (4;3), (5,2) és (6;1). Tehát 6 ilyen eset van.
Dobott számok összege 8: (2;6), (3;5), (4;4), (5;3), és (6,2). Tehát 5 ilyen eset van.

Mivel két kockával dobva, összesen 36 lehetőség van, ezért az A⋅B esemény valószínűsége: \( P(A·B)=\frac{20}{36}=\frac{5}{9}≈0.56. \)Így a \( \frac{P(A·B)}{P(B)} \) hányados értéke: \( \frac{P(A·B)}{P(B)}=\frac{20}{36}:\frac{30}{36}=\frac{20}{30}≈0.67 \).

Ez a hányados azt fejezi ki, hogy 20 esetben fordul elő, hogy az összeg legalább 5 és legfeljebb 8, de az összes lehetőség most nem 36, hanem csak 30, a „B” esemény bekövetkezésének a száma.

Lásd az alábbi táblázatot. Vastagítva a kedvező esetek. Felülhúzás jelöli azokat az eseteket, amikor a „B” esemény nem következik be.

	1	2	3	4	5	6
1	\( \overline{2} \)	\( \overline{3} \)	\( \overline{4} \)	5	6	7
2	\( \overline{3} \)	\( \overline{4} \)	5	6	7	8
3	\( \overline{4} \)	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

Így elmondhatjuk, hogy annak a valószínűsége, hogy két kockával dobott számok összege legfeljebb 8, feltételezve hogy a dobott számok összege legalább 5: \( \frac{P(A·B)}{P(B)}=\frac{20}{36}:\frac{30}{36}=\frac{20}{30}≈0.67 \)

A \( \frac{P(A·B)}{P(B)} \) hányados az „A” esemény bekövetkezésének a valószínűségét adja, feltételezve, hogy a „B” esemény bekövetkezett.

Definíció:

Legyen „H” egy eseménytér, „B” pedig egy olyan esemény, amelyre igaz, hogy P(B)≠0. Bármely „A” esemény „B” feltétel melletti feltételes valószínűsége: \( P(A|B)=\frac{P(A·B)}{P(B)} \).

A \( P(A|B) \) az „A” eseménynek „B” eseményre vonatkoztatott valószínűségét jelöli.

Természetesen általában \( P(A|B) \)≠\( P(B|A) \) .

A fenti definíciót átrendezve a P(A⋅B)=P(A|B)⋅P(B) szorzat alakot kapjuk.

Belátható, hogy a feltételes valószínűségre teljesülnek az alábbi relációk:

0≤P(A|B)≤1
P(B|B)=1
P((A+B)|C)=P(A|C)+P(B|C)-P((AB)|C)

Amennyiben „A” és „B” egymást kizáró események, azaz ha P(AB)=0, akkor P((A+B)|C)=P(A|C)+P(B|C).

A feltételes valószínűség összefüggését szorzat alakba írva:

P(A⋅B)=P(A|B)⋅P(B)
P(B⋅A)=P(B|A)⋅P(A)

Mivel P(A⋅B)=P(B⋅A), ezért a fenti két összefüggésből kapjuk az un. szorzási szabályt:

P(A|B)⋅P(B)=P(B|A)⋅P(A).

Post Views: 8 323