Definíció:
Ha az \( \vec{a} \) vektor nem nullvektor (\( |\vec{a}|≠0 \)), akkor az \( \vec{a} \) vektor és a λ valós szám (λ∈ ℝ) szorzata a λ⋅ \( \vec{a} \) vektor olyan az \( \vec{a} \) vektorral egyállású (párhuzamos) vektor amelynek abszolút értéke (hossza) az eredeti vektor abszolút értékének (hosszának) λ szorosa. (azaz \( |λ·\vec{a}|=|λ|·|\vec{a}| \)) vektor.
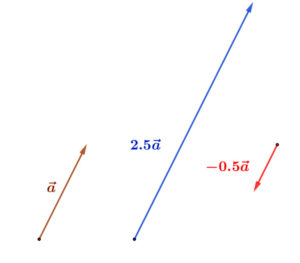Pozitív számmal (λ>0) történő szorzás esetén a λ⋅ \( \vec{a} \) vektor iránya megegyezik az \( \vec{a} \) vektor irányával.
Negatív számmal (λ<0) történő szorzás esetén pedig a λ⋅ \( \vec{a} \) vektor az a vektorral ellentétes irányú.
Nullával (λ=0) történő szorzás esetén az eredmény nullvektor, amelynek iránya és állása tetszőleges.
Nullvektor (|\( \vec{a} \) |=0) bármilyen λ valós számmal (λ∈ ℝ) történő szorzása esetén az eredmény is nullvektor.
Comments are closed, but trackbacks and pingbacks are open.