A valószínűségeloszlás fogalma.
A valószínűségi változóval, mint a kísérlet kimenetelének numerikus jellemzőjével összefüggésben elsősorban az érdekel minket, hogy a lehetséges értékeket milyen valószínűséggel veszi fel.
Egy lövész mesterségbeli tudására nyilván az a jellemző, hogy milyen valószínűséggel ér el 10-es; 9-es stb. találatot.
Ha ξ–vel jelöljük találat értékét jelző valószínűségi változót, amelynek lehetséges értékei x1; x2; x3;…; xn;… és tudjuk, hogy ezeket p1; p2; p3;…;pn valószínűségekkel veszi fel, akkor azt mondjuk, hogy ismerjük a ξ valószínűségi változó eloszlását, amelyet diszkrét valószínűségi változó esetében egy táblázattal is megadhatunk.
Példa:
Dobjunk fel kétszer egy szabályos pénzérmét! Minden fej dobásakor 100 Ft-t nyerünk és minden írás dobáskor 100 Ft-t veszítünk. A ξ valószínűségi változó jelentse a pénznövekedésünket a dobások után.
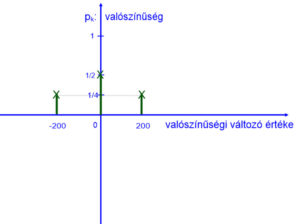
Ennél a kísérletnél az eseménytér 4 darab elemi eseményből áll. A1={i;i}, A2={i;f}, A3={f;i}, A4={f;f}. Ekkor a ξ valószínűségi változó értékei: ξ(A1)=-200=x1, ξ(A2)=0=x2=ξ(A3), ξ(A4)=200=x3.
Az egyes valószínűségi változókhoz tartozó valószínűségek:
P(ξ=-200=x1)=1/4=0,25. Két írás dobása esetén ennyi a valószínűsége annak, hogy veszítünk.
P(ξ=0=x2)=1/2=0,50. Két olyan elemi esemény is van, ahol se nem nyerünk, se nem veszítünk. Így ennek valószínűsége 0,5.
P(ξ=200=x3)=1/4=0,25. Ennyi a valószínűsége annak, hogy nyerünk 200 Ft.
Ezt tartalmazza az alábbi táblázat:
|
Elemi esemény |
Valószínűségi változó és annak eloszlása |
|
|
A1={i;i} |
ξ(A1)=-200=x1 |
P(ξ=-200=x1)=1/4=0,25 |
|
A2={i;f} |
ξ (A2)=0=x2 | P(ξ=0=x2)=1/2=0,50 |
|
A3={f;i} |
ξ (A3)=0=x2 |
|
| A4={f;f} | ξ (A4)=200=x3 |
P(ξ=200=x3)=1/4=0,25 |
Ennek a ξ valószínűségi változónak az eloszlását ábrázolhatjuk grafikonon is.
Definíció:
Legyenek egy valószínűségi kísérlethez rendelt ξ valószínűségi változó lehetséges értékeinek halmaza {x1; x2;…xn…}. Ekkor a P(ξ=xi) valószínűségek halmazát a ξ valószínűségi változó eloszlásának nevezzük.
Feladat:
Két kockával dobunk és a kapott számpárokhoz (elemi eseményekhez) hozzárendeljük a dobott számok összegét. Számítsuk ki az egyes összegekhez tartozó valószínűségeket! A kapott eredményeket állítsuk össze egy táblázatban és szemléltessük grafikonon!
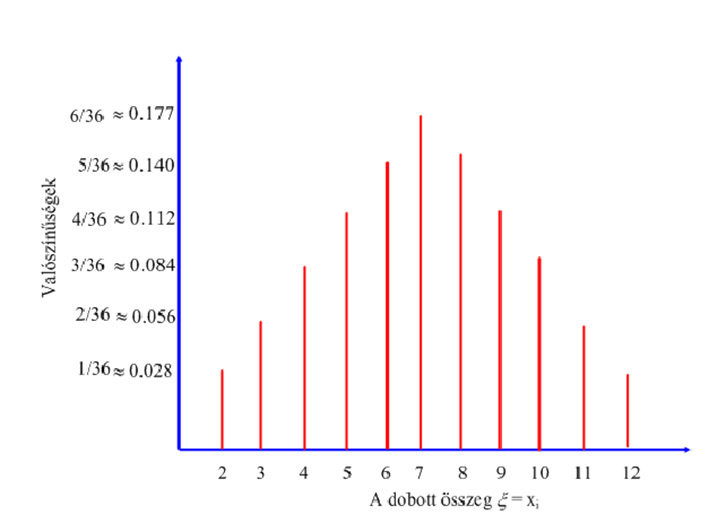
Az eseménytér elemeinek a száma: 36.
A valószínűségi változók száma 11, dobott számok összegének lehetséges értékei: [2;12] .
Táblázatban:
|
Elemi események |
Elemi események száma | A valószínűségi változó ξ(xi)= a dobott összeg |
Valószínűségek P(ξ=xi) |
|
|
(1;1) |
1 |
ξ=2=x1 |
1/36= |
0,028 |
| (1;2), (2;1) |
2 |
ξ=3=x2 |
2/36 |
0,056 |
| (1;3), (2;2), (3;1) |
3 |
ξ=4=x3 |
3/36= |
0,083 |
| (1;4), (2;3), (3;2), (4;1) |
4 |
ξ=5=x4 |
4/36= |
0,111 |
| (1;5), (2;4), (3;3); 4;2), (5;1)) |
5 |
ξ=6=x5 |
5/36= |
0,139 |
| (1;6), (2;5), (3;4), (4;3), (5;2), (6;1) |
6 |
ξ=7=x6 |
6/36= |
0,167 |
| (2;6), (3;5), (4;4), (5;3), (6;2), |
5 |
ξ=8=x7 |
5/36= |
0,139 |
| (3;6), (4;5), (5;4), (6;3) |
4 |
ξ=9=x8 |
4/36= |
0,111 |
| (4;6); (5;5), (6;4) |
3 |
ξ=10=x9 |
3/36= |
0,083 |
| (5;6), (6;5) |
2 |
ξ=11=x10 |
2=116 |
0,056 |
| (6;6) |
1 |
ξ=12=x11 |
1/36= |
0,028 |
| Összesen: | 36 | Összesen: | 1 | |
A valószínűségi változókhoz rendelt valószínűségek összege: \( \sum_{i=1}^{11}{P(ξ=x_{i})=1 } \) .
Grafikonon (Valószínűségdiagram):
Comments are closed, but trackbacks and pingbacks are open.