Szögharmadolás

Ez is egyike a nevezetes ókori matematikai problémáknak. Többek között már  Arkhimédész és Eratoszthenész is foglalkozott vele.

Szögharmadolás euklideszi értelemben vett eljárással nem lehetséges.

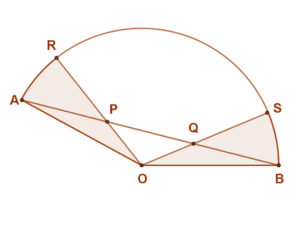Az első ötlet talán az lehetne a szög harmadolása érdekében, hogy harmadoljuk el a szög ívéhez tartozó húrt. Belátható, hogy ez nem fogja a szöget harmadolni.A mellékelt ábrán ezt próbáljuk szemléltetni. Az AB húrt harmadolja a P és a Q pont, azaz AP=PQ=QB. Ugyanakkor az OP és OQ egyenesek nem harmadolják az AB ívet és nem harmadolják az AOB∠-t.

Bár tetszőleges szögre nincs euklideszi értelemben vett eljárás, azért persze vannak olyan szögek, amelyek harmadolhatók. (90°, 45°, stb.)

Szögharmadolás nem euklideszi értelemben vett eljárással.

Ha nem ragaszkodunk az euklideszi értelemben vett szerkesztéshez, akkor a szögharmadolás lehetséges. Már az ókorban Arkhimédész is adott egy eljárást szögharmadolásra.

 

Legyen adott egy tetszőleges α szög, amit el szeretnénk harmadolni.

 

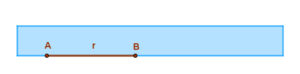Ennél az eljárásnál szükségünk van egy vonalzóra, amelyen egy előre kijelölt tetszőleges AB=r távolság van bejelölve.

 

Hosszabbítsuk meg az adott szög egyik szárát.

 

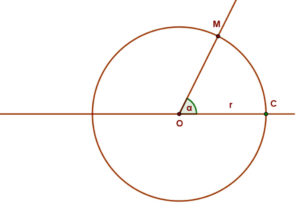
A szög csúcsa (O) körül a vonalzón felvett (r) távolsággal, mint sugárral húzzunk egy kört. Ez metszi a szög másik szárát egy M pontban.

Helyezzük el a vonalzónkat úgy, hogy a vonalzónk éle áthaladjon az M ponton, B pontja a körívre, A pontja pedig a szögszár meghosszabbításán legyen. Az így létrejött BAO∠=ß szög éppen az adott α szög harmada.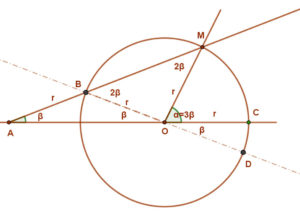

Ennek belátásához nézzük a mellékelt ábrát.  Húzzunk egy egyenest a B és O pontokon át. A vonalzó elhelyezése után így kapott  BAO∇ egyenlőszárú., hiszen AB=r=BO. Ennek a háromszögnek az OBM∠ külső szöge, emiatt OBM∠=2ß.

Mivel az OBM∇ is egyenlőszárú, a BMO∠=2ß. Ennek a ∇ -nek a DOM∠ külső szöge, tehát DOM∠=4ß. Mivel DOC∠=ß szintén (AOB∠ csúcsszöge), ezért α=3ß kell legyen.

Így tehát a ß szög éppen az α szög harmada.