Ma már megszokott dolog, hogy a nyomtatott vagy az elektronikus sajtóban táblázatokkal és grafikonokkal találkozunk.
Ezeket az adatokat persze előbb össze kellett gyűjteni és rendszerezni.
Az adatok diagramokban történő ábrázolása vizuális lehetőséget ad egy áttekintőbb értékelésre.
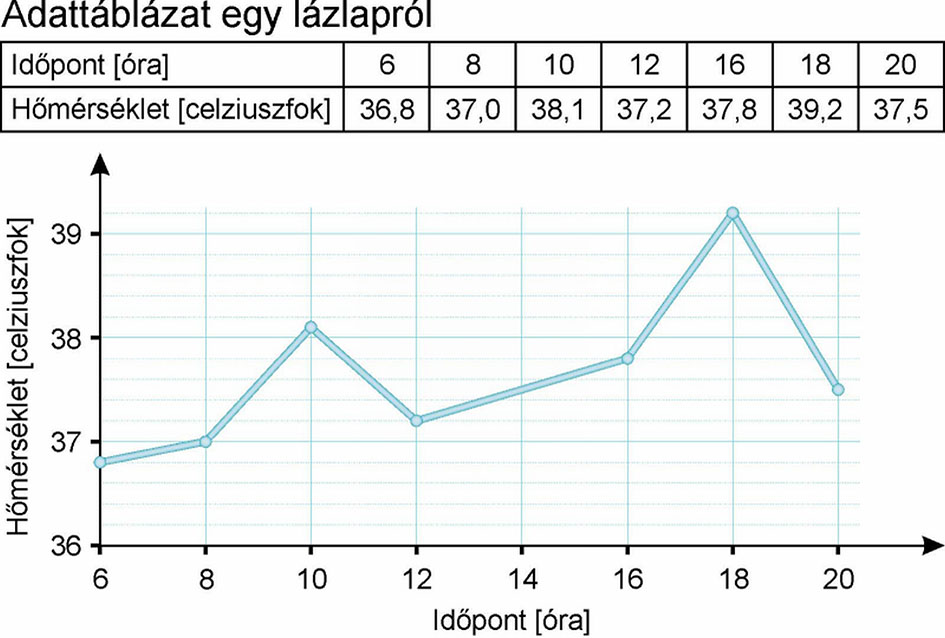
Régebbi időkben használt lázlapok visszatükrözték a beteg állapotának a változását.
Ebben az esetben itt az un. vonaldiagramot alkalmazták.
A mellékelt táblázat egy koordináta-rendszerhez hasonlítható. A vízszintes tengelyen az időpont, a függőleges tengelyen pedig a beteg hőmérséklete látható. Ez utóbbi a függvény érték, amely az időpont (mint változó) függvénye. Itt a vonaldiagram folytonos, hiszen a változó (az idő) is folytonos. Igaz, hogy az egyes mérésék csak egy-egy adott időpillanatra vonatkoznak.
Mielőtt nekiállunk agy adott feladatnál a diagram elkészítéséhez, szembetaláljuk magunkat a méretezés problémájával. Az érték tengely skálázásához is szükséges az adatmennyiség terjedelmének a meghatározása.
Definíció:
Az adatsokaság terjedelme a legnagyobb és a legkisebb adatának a különbsége.
Egy 1996. évi felmérésben a következő adatokat kapták:
| 8 általánosnál kevesebb: | 2,8 Millió |
| 8 általános: | 2,8 Millió |
| Szakmunkás: | 1,6 Millió |
| Érettségi: | 1,9 Millió |
| Felsőfokú: | 0,9 Millió |
Fel is „szisszenhetnénk”, mivel túl soknak tűnik a 8 általánosnál kevesebb 2,8 millió lakos.
Azonban ha összeadjuk az adatokat, ez éppen 10 millió lesz.
Ebből az következik, hogy abban a 2,8 millió 8 általánosnál kevesebb lakosban benne vannak a csecsemők és az óvodások is. Így már árnyaltabb a kép.
Ez is egy jó példa arra, hogy jól meg kell tervezni a felmérést és ha egy ilyen táblázattal vagy diagrammal találkozunk, jól meg kell fontolni, milyen következtetést vonunk le belőle.
A fenti adatsokaság terjedelme= 2.8⋅106-0.9⋅106=1.9⋅106. Ezért az érték tengelyen 1 egység 106 azaz 1 millió legyen.
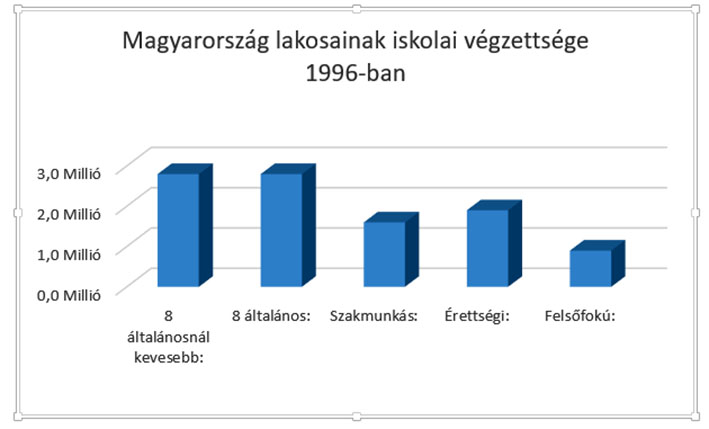
A mellékelt un. oszlopdiagram a fenti táblázat alapján készült. Ebben az esetben nem jöhet szóba a vonaldiagram, hiszen a változók (az ismérvek, az iskolai végzettség) diszkrét, nem folytonos értékek.
Az iskolai életben nagyon gyakori, hogy egy osztály vagy évfolyam dolgozatairól (teljesítményéről) is készül táblázat és diagram. Hány 5-ös, 4-es, 3-as, 2-es és 1-es dolgozat született. Itt a változó az osztályzat, míg az érték az osztályzat előfordulásának a száma, azaz a gyakorisága.
A gyakorisági diagramokat szokás hisztogramoknak is nevezni. (A fenti diagram is tekinthető hisztogramnak.)
Ha a gyakoriság értékét az adatok összegéhez (100%) viszonyítjuk, akkor a relatív gyakoriságot kapjuk.
Egy osztály matematika dolgozatának eredményeit tartalmazza a következő táblázat:
| Gyakoriság | Relatív gyakoriság | |
| 5-ös | 2 Fő | 10% |
| 4-es | 5 Fő | 25% |
| 3-as | 6 Fő | 30% |
| 2-es | 3 Fő | 15% |
| 1-es | 4 Fő | 20% |
| Összesen: | 20 Fő | 100% |
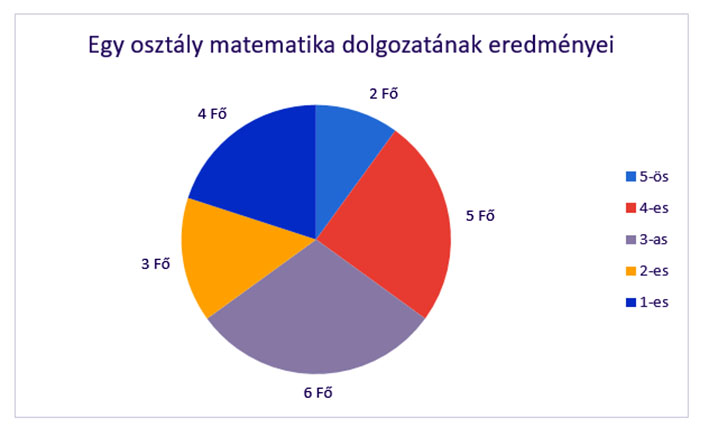 Ezt ábrázolhatjuk kördiagramban is:
Ezt ábrázolhatjuk kördiagramban is:
Itt az egyes gyakoriságokat egy körcikk képviseli.
Szükség lehet arra, hogy mi magunk „kézzel” készítsünk kördiagramot, sőt az előfordulhat, hogy egy adott kördiagramról határozzuk meg az adatok értékét.
A körcikk középponti szögének értéke mértéke egyenesen arányos az adat értékével. Tehát a középponti szög=(360/100)⋅relatív gyakoriság)
A fenti faladatban tehát az egyes osztályzatokhoz tartozó körcikkek középponti szögeinek értékét a következő kibővített táblázat tartalmazza.
| Gyakoriság | Relatív gyakoriság | Középponti szög | |
| 5-ös | 2 Fő | 10% | 36,0° |
| 4-es | 5 Fő | 25% | 90,0° |
| 3-as | 6 Fő | 30% | 108,0° |
| 2-es | 3 Fő | 15% | 54,0° |
| 1-es | 4 Fő | 20% | 72,0° |
| Összesen: | 20 Fő | 100% | 360,0° |
Feladat:
A 12. évfolyam tanulói magyarból próba érettségit írtak. Minden tanuló egy kódszámot kapott, amely az 1, 2, 3, 4 és 5 számjegyekből mindegyiket pontosan egyszer tartalmazta valamilyen sorrendben.
a) Hány tanuló írta meg a dolgozatot, ha az összes képezhető kódszámot mind kiosztották?
b) Az alábbi kördiagram a dolgozatok eredményét szemlélteti:
Adja meg, hogy hány tanuló érte el a szereplő érdemjegyeket! Válaszát foglalja táblázatba, majd a táblázat adatait szemléltesse oszlopdiagramon is!
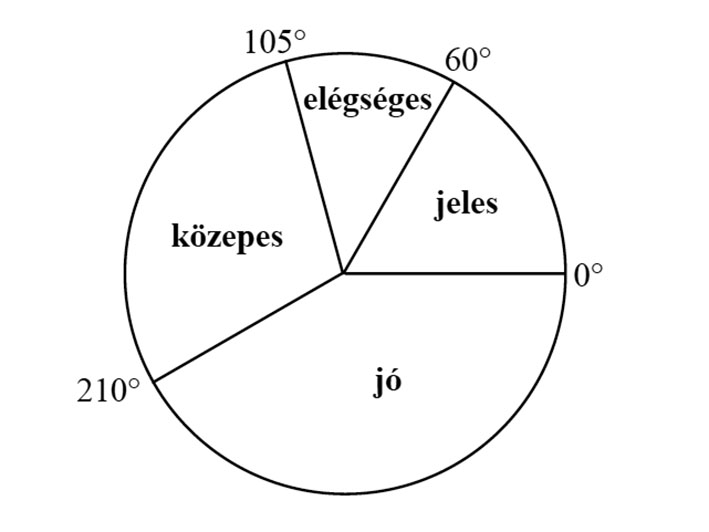
c) Az összes megírt dolgozatból véletlenszerűen kiválasztunk egyet. Mennyi a valószínűsége annak, hogy jeles vagy jó dolgozatot veszünk a kezünkbe?
Ez a feladat a 2006. évi középszintű feladatsor 15. sorszámú 12 pontos példája volt.
Megoldás:
a) Az első kérdés egy kombinatorikai meggondolást igényel. Az 1, 2, 3, 4 és 5 számjegyeket 5⋅4⋅3⋅2⋅1= 5! =120 féleképpen lehet sorbarendezni (permutálni). Tehát a magyar próbaérettségit 120 tanuló írta meg.
Ezért 3 pont járt az érettségin.
b) Tehát 120 adathoz tartozik a 360°-os középponti szög és a 100%-os relatív gyakoriság.
| Középponti szög | Gyakoriság | Relatív gyakoriság |
|
| 5-ös | 60° | (60/360)⋅120=20 fő | ≈ 17% |
| 4-es | 150° | (150/360)⋅120=50 fő | ≈41.5% |
| 3-as | 105° | (105/360)⋅120=35 fő | ≈29% |
| 2-es | 45° | (45/360)⋅120=15 fő | =12.5% |
| 1-es | 0° | 0 fő | =0% |
| Összesen: | 360,0° | 120 fő | 100% |
Az oszlopdiagram: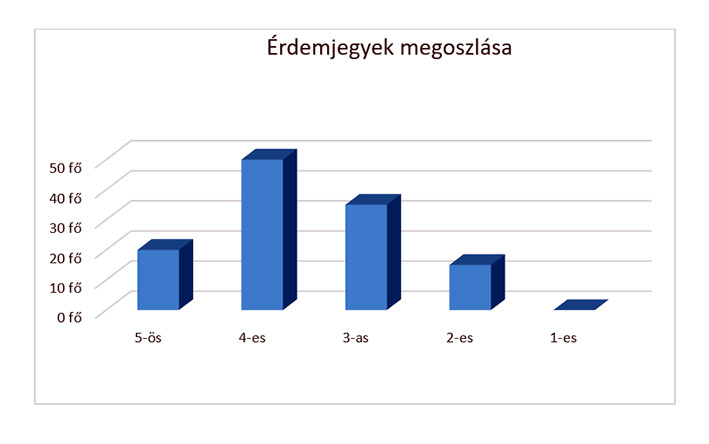
Ezért 6 pont járt az érettségin.
c) A 4-es és 5-ös érettségi összesen 70 dolgozat. Ez a 120 dolgozathoz viszonyítva: 70/120≈0,58.
Tehát a keresett valószínűség: ≈0,58, azaz ≈58%.
Ezért 3 pont járt az érettségin.
Ez a feladatsor is rámutat arra, hogy az egyes feladatok különböző matematikai szakterületeket is érinthetnek. Itt az alapvetően statisztikai feladat kombinatorikai és valószínűségszámítási részeket is magába foglalt.


Comments are closed, but trackbacks and pingbacks are open.