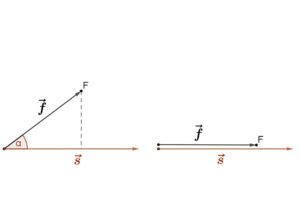
A fizikából ismert tény, hogy ha az erő és az elmozdulás azonos irányú, akkor az erő nagyságának és az elmozdulás nagyságának a szorzata adja a munka nagyságát: \( W=|\vec{F}|·|\vec{s}| \).
Itt az erő és az elmozdulás vektor jellegű mennyiségek, hiszen nagyságukon kívül az irányuk is jellemző rájuk, míg a munka csak számmal jellemezhető, azaz skaláris mennyiség.
Ha azonban az erő és az elmozdulás szöget zár be, akkor a munkavégzés nagyságát úgy kapjuk meg, hogy az erő és az elmozdulás nagyságát és a közbezárt szögük koszinuszának szorzata adja: \( W=|\vec{F}|·|\vec{s}|·cos(α) \) .
Definíció:
Két vektor skaláris szorzatán a két vektor abszolút értékének és hajlásszögük koszinuszának szorzatát értjük.
Formulával: \( \vec{a}·\vec{b}=|\vec{a}|·|\vec{b}|·cos(α) \) , ahol 0°≤α≤ 180° , a hajlásszög definíciójából következően.
Ha 0°≤α<90°, akkor a skaláris szorzat értéke pozitív valós szám.
Ha 90°< α ≤180°, akkor a skaláris szorzat értéke negatív valós szám.
Ha α=90°, akkor cos90°=0 miatt a skaláris szorzat értéke is nulla.
Két vektor szorzata tehát ebben az esetben nem vektor, hanem egy valós szám, azaz skalár.
Megjegyzés:
Ha két vektor közül az egyik, vagy mindkettő nullvektor, akkor ugyan hajlásszögük nem definiált egyértelműen, viszont a nullvektorok abszolút értéke nulla, következésképpen a skaláris szorzatuk is nulla. A skaláris szorzat definíciója tehát ebben az esetben is egyértelmű eredményt ad.
Tétel:
Két vektor skaláris szorzata akkor és csak akkor 0, ha a két vektor merőleges egymásra.
1. Ha a két vektor merőleges egymásra, akkor hajlásszögükre α=90° , így cos90°=0 miatt a skaláris szorzat értéke is nulla.
2. Nézzük most azt az esetet, hogy két vektor skaláris szorzata nulla.
Ha a vektorok nem nullvektorok, akkor skaláris szorzatuk csak akkor lehet nulla, ha cosα =0. Ez pedig azt jelenti, hogy α =90°, azaz a vektorok merőlegesek egymásra.
Ha a vektorok között nullvektor is szerepel, akkor mivel a nullvektorok iránya tetszőleges, ezért ebben az esetben is mondhatjuk, hogy merőlegesek egymásra.
Skaláris szorzás tulajdonságai:
1. A skaláris szorzat felcserélhető (kommutatív).
Azaz: \( \vec{a}·\vec{b}=\vec{b}·\vec{a} \).
Ez a definíció következménye, hiszen felcserélhetőség a valós számokra igaz.
2. Egy vektor önmagával való skaláris szorzatát a vektor négyzetének nevezzük.
Azaz: \( \vec{a}·\vec{a}=|\vec{a}|·|\vec{a}|·cos(0°)=|\vec{a}|^2 \) Mivel ekkor a hajlásszög nulla, ezért cos0° =1.
3. Bebizonyítható, hogy a skaláris szorzat az összeadásra nézve disztributív.
Azaz: \( \vec{c}·(\vec{a}+\vec{b})=\vec{c}·\vec{a}+\vec{c}·\vec{b} \).
4. Skaláris szorzatot egy számmal úgy is szorozhatunk, hogy a számmal a skaláris szorzat egyik tényezőjét szorozzuk.
Azaz: \( k·(\vec{a}·\vec{b})=(k·\vec{a})·\vec{b}=\vec{a}·(k·\vec{b}) \), ahol k∈ℝ.
5. A skaláris szorzat általában nem csoportosítható (nem asszociatív).
Azaz: \( (\vec{a}·\vec{b})·\vec{c}≠\vec{a}·(\vec{b}·\vec{c}) \).
Hiszen a mellékelt szorzásnál a baloldalon a \( \vec{c} \) vektor számszorosa \( (\vec{a}·\vec{b}) \)-szerese), míg a jobb oldalon az \( \vec{a} \) vektor számszorosa, \( (\vec{b}·\vec{c}) \)-szerese található.
A skaláris szorzás definícióját alkalmaztuk többek között a koszinusz tételnél, és az egyenes normálvektoros egyenletének levezetésekor.
Comments are closed, but trackbacks and pingbacks are open.